HDU/HDOJ acm 1030

hdu1030一道有规律的数学题，

仔细分析就可以得出结果，嘿嘿。。

作者：贾钰(Jeick Jia)   CS@SCU

时间：2011-4-25

Problem Description

A triangle field is numbered with successive integers in the way shown on the picture below.



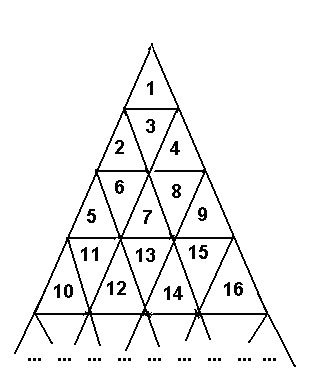
The traveller needs to go from the cell with number M to the cell with number N. The traveller is able to enter the cell through cell edges only, he can not travel from cell to cell through vertices. The number of edges the traveller passes makes the length of the traveller's route.

Write the program to determine the length of the shortest route connecting cells with numbers N and M.

 

 

 

Input

Input contains two integer numbers M and N in the range from 1 to 1000000000 separated with space(s).

 

 

Output

Output should contain the length of the shortest route.

 

 

Sample Input

   
   
   
   

    
    
    
    6 12
   
   
   
   

 

 

Sample Output

   
   
   
   

    
    
    
    3
   
   
   
   
 

 

题目的意思很明确，从一个格子到另一个格子最短需要穿过几次三角形的边。现在Jeick找出了它的规律，请开始听Jeick絮叨吧。

首先，每一层（lay）的数据是由特点的，最后面一个数字 n ,有关系 n = pow(lay,2)+1,对于第一个数字呢t,有关系 t =pow(lay-1,2).OK，根据这个关系呢，我们就可以求出任意一个数在这个塔中的层数：

               lay = (int)ceil(sqrt((double)n));

其中sqrt不用介绍吧，ceil函数功能是向上取整，有C++math库提供。

然后呢，我们再观察另一个规律left，left表示给出的数字在塔中 左上→右下 斜行中的第几行，例如1,3,2,6,5，……就是在一斜行，我们称之为left行，计算left：

              left  = (n-lay_first)/2+1

其中lay_first表示n所在层得第一个数字。

         有left规律，那么就得有right规律嘛，right规律的第一同理left，

              right = (lay_last-n)/2+1;

其中 lay_last表示n所在层得最后一个数字。

ok，我们的定义结束，现在就找这些定义之间的关系。

设有起始位置在   front  ，重点位置在   back

从图中我们可以看出，从front出发至back穿过的三角形边只有三种情况对吧，水平边，左边，右边，同时也会发现：

水平边等于 lay_front，lay_back的差值        △lay

左边等于    right_front, right_back的差值    △right

右边等于   left_front，left_back的差值        △left

于是结果就显而易见了：result = △lay+△right+△left

代码就很简单了，下面是我的代码：

#include<iostream>

#include<cmath>

using namespace std;

int main()

{

int front,back;

while(cin>>front>>back)

{

       int lay_front = (int)ceil(sqrt((double)front));

       int lay_back = (int)ceil(sqrt((double)back));

       int right_front = (front-(lay_front-1)*(lay_front-1)-1)/2+1;

       int right_back = (back-(lay_back-1)*(lay_back-1)-1)/2+1;

       int left_front = (lay_front*lay_front-front)/2+1;

       int left_back = (lay_back*lay_back-back)/2+1;

       cout<<abs(lay_front-lay_back)+abs(right_front- right_back)+abs(left_front-left_back)<<endl;

       }

return 0;

}