双调欧几里得旅行商问题

问题的描述如下(书中231页)：

平面上n个点，确定一条连接各点的最短闭合旅程。这个解的一般形式为NP的（在多项式时间内可以求出）。

J.L. Bentley 建议通过只考虑双调旅程(bitonic tours)来简化问题,这种旅程即为从最左点开始，严格地从左到右直至最右点，然后严格地从右到左直至出发点。下图(b)显示了同样的7个点的最短双调路线。在这种情况下，多项式的算法是可能的。事实上，存在确定的最优双调路线的O(n*n)时间的算法。

                       （a）                               (b)

（a）图是最短的闭合旅程，长度为24.89。（b）图是问题经简化后，同样的点集的最短双调闭合旅程，长度为25.58。

解题思路：

根据简化后的双调欧几里得旅行问题的性质，将点集依据各点x坐标单调递增来进行编号，我们设b[i,j]是最短双调闭合旅程P(i,j)的长度(i<=j)，而最短双条闭合旅程P(i,j)是指从点P[i]开始,严格地向左走（即是每次经过的点的x坐标都比前一个点的x坐标要小），直到最左点P[1],然后再严格向右走，直到终点P[j]为止，在从P[i]到P[j]过程中的点有且只经过一次。设distance[i,j]是点P[i]到P[j]之间的欧式距离。

那么，根据动态规划的方法，我们要找出问题的最优子结构，并且递归定义出来，下面是问题的公式（大前提是i<=j）：

b[1,2]=distance(1,2)；最小的子问题，主要用于求解更大的子问题；

b[i,j]=b[i,j-1] + distance(j-1,j),如果i<j-1；

b[i,j]=min{ b[k,j-1] + distance(k,j) }，其中1<=k<j-1,如果i=j-1；

下面讲解公式的由来，最短双调旅程P(i,j)在到达终点P[j]之前，正常来说，按照双调的概念，一定经过了一个其x坐标刚好比点P[j]小的点，也就是P[j-1](当然当i=j-1时就另当别论了),所以如果当i<j-1时，最短双调旅程P(i,j)的长度应该可以看成是其子问题P（i,j-1）的长度和点distance（j-1，j）的和。但是当i=j-1时，问题就不同了，因为我们不能一开始从点P[i]直接跳到P[j]，因为其他点都还没有走过一次,所以在到达终点P[j]的前一个点不能再是点P[j-1]（即P[i]），那如何是好呢？因为在到达终点P[j]之前肯定要经过一个点的，但不知道是哪个点，我们不妨设该点是P[k]，那么k的范围肯定是1<=k<j-1（因为是除了点P[j-1]和P[j]之外的点），当然该点P[k]要使得双调旅程P(i,j)的长度最短,于是在k的可能范围中找，于是再使用一个min操作。i=j-1时的情况类似于矩阵链乘的问题,其实这也是动态规划的惯用手法，假设一个最优选择，然后再基于该最优选择来定义问题。

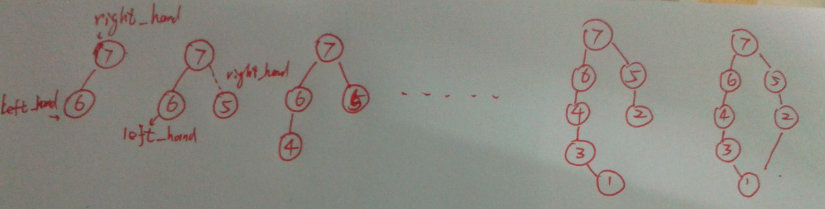
这相当于我们每次求解问题P(i,j)，都作了一次选择，要么是点P[j-1]或是点P[k]作为P[j]的前一个点，其示意图如下：

要知道，我们要求解的问题结果是b[n,n],于是

b[n,n]=b[n-1,n]+distance(n-1,n)；

这里要注意的一点，在之前的公式中，并不涉及求解类似b[i,i]的值,这里定义了b[i,i]的情况。

除此之外，还涉及到了对最优解的重构的问题。我们将使用一个r[i][j]数组表示子问题P(i,j)在到达终点P[j]之前经过的一个点P[k]对应的k值（仅挨着点P[j]的点），则子问题的解可以组织为其更小的子问题P（i，k）的解加上点P[k]和点P[j]。由之前的解题思路可知，对于问题P(i,j),当i=j-1时，k<i,当i<j-1时，k=j-1。

其实得到的最优解是个闭合旅程，所以从出发后的第一个点与到达之前的一个点的位置是等价的。如闭合旅程是76431257，也可以是75213467。

构造解的过程如下：

每次加入的点总是在序号大的点下，因为问题P(i,j)总是分解为子问题P(i,k),不管k是等于j-1，还是小于j-1，然后确定点P[k]是到达P[j]之前的一个点，这也是问题每次选择的结果。使用一个数组存放序号，一边从0开始，一边从末尾开始。

以下是问题的实现：

#include <iostream>
#include <cmath>
#include <fstream>
using namespace std;

#define N 7
struct Point{
    double x;
    double y;
};
struct Point points[N+1];
double b[N+1][N+1];
int r[N+1][N+1];


double distance(int i,int j);//第i，j点的欧式距离
double Euclidean_TSP();//最短闭合旅程长度
void my_print_path();//打印旅程

void main(int argc, char **argv){
    ifstream infile;
    infile.open("input.txt");//读入一个有各点坐标的文档
    if (!infile)
    {
        cout<<"error!"<<endl;
    }
    int i=1;
    while (infile>>points[i].x>>points[i].y)
    {
        i++;
    }
    cout<<"最短双调闭合旅程长度是："<<Euclidean_TSP()<<endl;
    my_print_path();
}

double distance(int i,int j){
    return sqrt((points[i].x-points[j].x)*(points[i].x-points[j].x)
        +(points[i].y-points[j].y)*(points[i].y-points[j].y));
}

double Euclidean_TSP(){
    b[1][2]=distance(1,2);//最小的子问题

    for (int j=3;j<=N;j++)
    {
        //i<j-1且i>=1时的情况
        for (int i=1;i<j-1;i++)
        {
            b[i][j] = b[i][j-1]+distance(j-1,j);
            r[i][j] = j-1;
        }
        //i=j-1的情况
        b[j-1][j] = b[1][j-1]+distance(1,j);//先设初值为k=1时的值
        r[j-1][j] = 1;
        for (int k=1;k<j-1;k++)
        {
            double q = b[k][j-1]+distance(k,j);
            if (q < b[j-1][j])
            {
                b[j-1][j] = q;
                r[j-1][j] = k;
            }
        }
    }
    b[N][N] = b[N-1][N]+distance(N-1,N);
    return b[N][N];
}

void my_print_path(){
    int string[N];
    string[0]=N;
    string[1]=N-1;
    int k=N-1;
    int left_hand=N-1,right_hand=N,begin=2,end=N-1;
    for (int i=N-1,j=N;k!=1;)
    {
        k=r[i][j];
        if (left_hand>right_hand) //比较那边的点的序号大
        {
            left_hand=k;
            string[begin]=k;
            begin++;
        }else{
            right_hand=k;
            string[end]=k;
            end--;
        }
        if (i==j-1)
        {
            j=i;
            i=k;
        }else if (i<j-1)
        {
            j=k;
        }
    }
    cout<<"该旅程是：";
    for (int index=0;index<N;index++)
    {
        cout<<string[index];
    }
    cout<<endl;
}

input.txt:

 

0 6

1 0

2 3

5 4

6 1

7 5

8 2

 

运行后：

最短双调闭合旅程长度是：25.584

该旅程是：7643125

其实旅程也可以是7521346