解析Linux环境下RAID 6的Q校验算法
【前言】
RAID为廉价磁盘冗余阵列(Redundant Array of Inexpensive Disks),RAID技术将一个个单独的磁盘以不同的组合方式形成一个逻辑硬盘,从而提高了磁盘读取的性能和数据的安全性。不同的组合方式用RAID级别来标识,常见RAID的级别有0、1、01、10、5、6等等。具体实现的数据存储的原理请参考相关文章。本章主要概述Linux环境下RAID 6级别的存储原理。Linux环境下配置RAID的命令是“mdadm”,如果不知道该命令如何使用请参考文章《Linux系统中实现RAID卷详解》。
【RAID 6概述】
RAID 6是指带有两种分布存储的奇偶校验码(既P和Q)的独立硬盘结构。与RAID 5相比,RAID 6增加了第二个独立校验码(Q)信息块,两个独立的奇偶校验系统使用不同的算法,数据的可靠性非常高,即使两块硬盘同时失效也不会影响数据的使用,主要是用于要求数据绝对安全的场合。如下图:
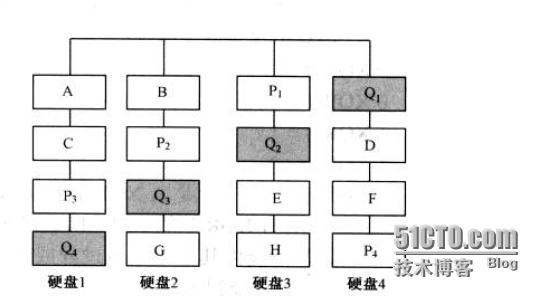
上图中Q为RAID 6的第二个校验信息块,采用的是非常复杂的“伽罗华域”算法,稍后会讲到。
【RAID 6的P校验概述】
其实RAID 6的P校验和RAID 5的校验是一样的,都是采用的“异或”运算。异或运算符的原则就是相同为0,不同为1的。在RAID 5的环境中只能掉一块硬盘,但是RAID 6在RAID 5的基础上添加了Q校验,因此RAID 6支持同时掉两块盘。异或运算如下:
P = A + B + C = A xor B xor C
A = P - B - C = P xor B xor C
注意:上述的加减法都是异或运算。
【RAID 6的Q校验概述】
说到Q校验就有点复杂了,它采用上面所提到的“伽罗华域”算法。“伽罗华域”实际上就是“0-255”的一个有限域GF(2^8),在GF(2^8)内不管是是加、减、乘、除都不会超过这个范围。并且,加减法可逆,乘除法可逆,而且计算的值在GF(2^8)内是唯一的。注意:此处提到的加、减、乘、除法不是日常使用的加减乘除,而是“伽罗华域”内的运算。在GF(2^8)中,如果2的n次方大于某个值(本原多项式)就会对该值(本原多项式)取余,结果又会返回到GF(2^8)中。因此,保证了2^0到2^255的结果值在GF(2^8)内是唯一的。
在GF(2^8)中一共有16个本原多项式,分别如下:
1 x8+x7+x6+x5+x4+x2+1 1 1111 0101 = 0x1F5
2 x8+x7+x6+x5+x2+x+1 1 1110 0111 = 0x1E7
3 x8+x7+x6+x3+x2+x+1 1 1100 1111 = 0x1CF
4 x8+x7+x6+x+1 1 1100 0011 = 0x1C3
5 x8+x7+x5+x3+1 1 1010 1001 = 0x1A9
6 x8+x7+x3+x2+1 1 1000 1101 = 0x18D
7 x8+x7+x2+x+1 1 1000 0111 = 0x187
8 x8+x6+x5+x4+1 1 0111 0001 = 0x171
9 x8+x6+x5+x3+1 1 0110 1001 = 0x169
10 x8+x6+x5+x2+1 1 0110 0101 = 0x165
11 x8+x6+x5+x+1 1 0110 0011 = 0x163
12 x8+x6+x4+x3+x2+x+1 1 0101 1111 = 0x15F
13 x8+x6+x3+x2+1 1 0100 1101 = 0x14D
14 x8+x5+x3+x2+1 1 0010 1101 = 0x12D
15 x8+x5+x3+x+1 1 0010 1011 = 0x12B
16 x8+x4+x3+x2+1 1 0001 1101 = 0x11D
RAID 6常用的本原多项式为0X11D,既上列中最后一个。Linux 环境中的RAID 6也是如此。
好了回到Q校验上,Q校验和P校验结合正好组成了一个二元一次方程,K1、K2、K3为GF(2^8)中多项式的数值。
P = A + B + C
Q = A*K1 + B*K2 + C*K3
【伽罗华域的乘除法运算】
伽罗华域中的加减法也是异或运算,所以就不做详细解释了,重点解释一下乘除法。通过上面的Q校验知道Q校验的生成需要伽罗华域中的乘法运算,计算乘法运算是一件非常复杂的事情,最好的解决办法就是将GF(2^8)中所有多项式的值生成表格,通过查表得知乘法运算的值。
1、生成正表GFILOG
通过下表的方法生成正表GFILOG,注意:此表的本原多项式为0X11D。

如下:是正表GFILOG

2、生成反表GFLOG
有了正向变换表,要得到逆向表就很简单了,把正向中的表变换值做为索引,在把正向表中的索引作为值就OK了。如下表:
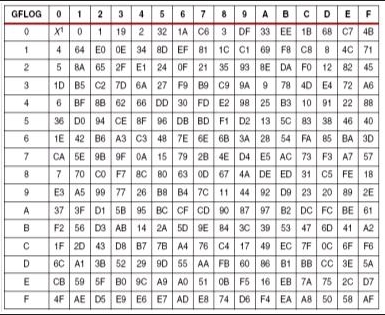
3、计算乘除法运算(查表法)
乘法:A * K1 = GFILOG[(GFLOG[A]+GFLOG[K1]) mod 255];
除法:A / K1 = GFILOG[(GFLOG[A]-GFLOG[K1]+255) mod 255];
现在知道了伽罗华域的乘除法,那么我们计算Q校验就方便了许多。
【根据Q校验生成丢失的数据】
当RAID 6中坏掉两块磁盘,那该如何生成丢失的数据呢?用RAID 6的一个条带举例说明。
1、如果某个条带中丢失的两块数据是P和Q,那么正好,数据没有丢失,正常提取即可。
2、如果某个条带中丢失的两块数据是P和A,那么可以根据Q校验计算出A的数据。
P = A*K1 + B*K2 + C*K3
A*K1 = P + B*K2 + C*K3
A = (P + B*K2 + C*K3)/ K1 //注:K1可以同过查表获取
3、如果某个条带中丢失的两块数据是Q和A,那么可以根据校验P计算出A的数据。
P = A + B + C
A = P + B + C
4、如果某个条带中丢失的两块数据是A和B,那么可以根据校验P和Q计算出A和B的数据。
P = A + B + C
Q = A*K1 + B*K2 + C*K3
A = P + B + C
Q = (P + B + C)*K1 + B*K2 +C*K3
Q = P*K1 + B*K1 + C*K1 + B*K2 + C*K3
Q = P*K1 + C*K1 + C*K3 + B*K1 + B*K2
Q + P*K1 + C*K1 + C*K3 = (K1+K2) * B
B = ( Q + P*K1 + C*K1 + C*K3) / (K1+K2)
计算出B的值以后,再根据P校验和计算出A的值就容易很多了。
A = P + B + C
【Linux环境下的RAID 6】
根据前的内容已经知道RAID 6的大致原理了。因为伽罗华域的本原多项式有16种,因此RAID 6的种类有很多,再加上K值的不固定。因此计算某个RAID 6的Q校验值会变的很复杂。不过Linux环境下的RAID 6的K值经过测试,其值根据够成RAID 6阵列的磁盘数,从本原多项式0X11D的开始取(RAID 6总磁盘数 -2)个多项式的值作为K的值。