使用SciPy插值，Interpolation (scipy.interpolate)

插值是进行数据处理和可视化分析的常见操作，基于Python的SciPy支持一维和二维的插值运算。

这里是SciPy的官方文档。

Contents(原文，英文索引)

• Interpolation (scipy.interpolate)

• 1-d Example

• 2-d Example

• Spline interpolation in 1-d: Procedural (interpolate.splXXX)

• Spline interpolation in 1-d: Object-oriented (UnivariateSpline)

• Two-dimensional spline representation: Procedural (bisplrep)

• Two-dimensional spline representation: Object-oriented (BivariateSpline)

• 1-D interpolation (interp1d)

• Multivariate data interpolation (griddata)

• Spline interpolation

• Using radial basis functions for smoothing/interpolation

There are several general interpolation facilities available in SciPy, for data in 1, 2, and higher dimensions:

• A class representing an interpolant (interp1d) in 1-D, offering several interpolation methods.

• Convenience function griddata offering a simple interface to interpolation in N dimensions (N = 1, 2, 3, 4, ...). Object-oriented interface for the underlying routines is also available.

• Functions for 1- and 2-dimensional (smoothed) cubic-spline interpolation, based on the FORTRAN library FITPACK. There are both procedural and object-oriented interfaces for the FITPACK library.

• Interpolation using Radial Basis Functions.

1-D interpolation (interp1d)

The interp1d class in scipy.interpolate is a convenient method to create a function based on fixed data points which can be evaluated anywhere within the domain defined by the given data using linear interpolation. An instance of this class is created by passing the 1-d vectors comprising the data. The instance of this class defines a __call__ method and can therefore by treated like a function which interpolates between known data values to obtain unknown values (it also has a docstring for help). Behavior at the boundary can be specified at instantiation time. The following example demonstrates its use, for linear and cubic spline interpolation:

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import interp1d

x = np.linspace(0, 10, num=11, endpoint=True)
y = np.cos(-x**2/9.0)
f = interp1d(x, y)
f2 = interp1d(x, y, kind='cubic')

xnew = np.linspace(0, 10, num=41, endpoint=True)

plt.plot(x, y, 'o', xnew, f(xnew), '-', xnew, f2(xnew), '--')
plt.legend(['data', 'linear', 'cubic'], loc='best')
plt.show()

Multivariate data interpolation (griddata)

Suppose you have multidimensional data, for instance for an underlying function f(x, y) you only know the values at points (x[i], y[i])that do not form a regular grid.

Suppose we want to interpolate the 2-D function

def func(x, y):
     return x*(1-x)*np.cos(4*np.pi*x) * np.sin(4*np.pi*y**2)**2

on a grid in [0, 1]x[0, 1]

grid_x, grid_y = np.mgrid[0:1:100j, 0:1:200j]

but we only know its values at 1000 data points:

points = np.random.rand(1000, 2)
values = func(points[:,0], points[:,1])

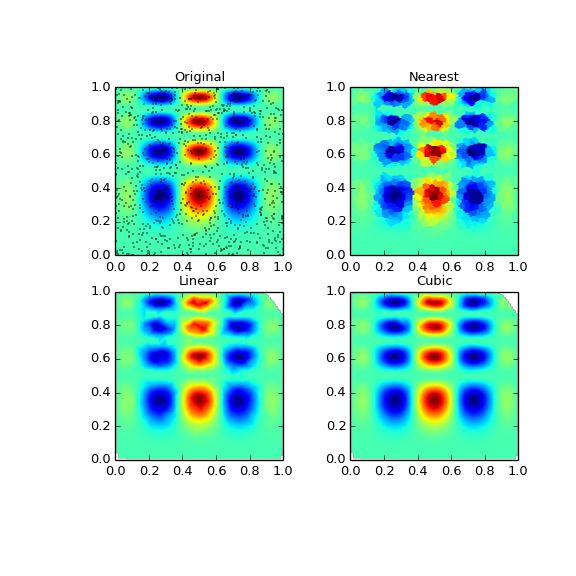
This can be done with griddata – below we try out all of the interpolation methods:

from scipy.interpolate import griddata
grid_z0 = griddata(points, values, (grid_x, grid_y), method='nearest')
grid_z1 = griddata(points, values, (grid_x, grid_y), method='linear')
grid_z2 = griddata(points, values, (grid_x, grid_y), method='cubic')

One can see that the exact result is reproduced by all of the methods to some degree, but for this smooth function the piecewise cubic interpolant gives the best results:

import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import interp1d

plt.subplot(221)
plt.imshow(func(grid_x, grid_y).T, extent=(0,1,0,1), origin='lower')
plt.plot(points[:,0], points[:,1], 'k.', ms=1)

plt.title('Original')
plt.subplot(222)
plt.imshow(grid_z0.T, extent=(0,1,0,1), origin='lower')

plt.title('Nearest')
plt.subplot(223)
plt.imshow(grid_z1.T, extent=(0,1,0,1), origin='lower')

plt.title('Linear')
plt.subplot(224)
plt.imshow(grid_z2.T, extent=(0,1,0,1), origin='lower')

plt.title('Cubic')
plt.gcf().set_size_inches(6, 6)
plt.show()

Spline interpolation

Spline interpolation in 1-d: Procedural (interpolate.splXXX)

Spline interpolation requires two essential steps: (1) a spline representation of the curve is computed, and (2) the spline is evaluated at the desired points. In order to find the spline representation, there are two different ways to represent a curve and obtain (smoothing) spline coefficients: directly and parametrically. The direct method finds the spline representation of a curve in a two- dimensional plane using the function splrep. The first two arguments are the only ones required, and these provide thexx and yy components of the curve. The normal output is a 3-tuple, (t,c,k)(t,c,k) , containing the knot-points,tt , the coefficients cc and the order kk of the spline. The default spline order is cubic, but this can be changed with the input keyword, k.

For curves in NN -dimensional space the functionsplprep allows defining the curve parametrically. For this function only 1 input argument is required. This input is a list of NN -arrays representing the curve in NN -dimensional space. The length of each array is the number of curve points, and each array provides one component of theNN -dimensional data point. The parameter variable is given with the keword argument, u, which defaults to an equally-spaced monotonic sequence between 00 and 11 . The default output consists of two objects: a 3-tuple, (t,c,k)(t,c,k), containing the spline representation and the parameter variableu.u.

The keyword argument, s , is used to specify the amount of smoothing to perform during the spline fit. The default value of ss iss=m−2m‾‾‾√s=m−2m where mm is the number of data-points being fit. Therefore, if no smoothing is desired a value ofs=0s=0 should be passed to the routines.

Once the spline representation of the data has been determined, functions are available for evaluating the spline (splev) and its derivatives (splev, spalde) at any point and the integral of the spline between any two points (splint). In addition, for cubic splines ( k=3k=3) with 8 or more knots, the roots of the spline can be estimated (sproot). These functions are demonstrated in the example that follows.

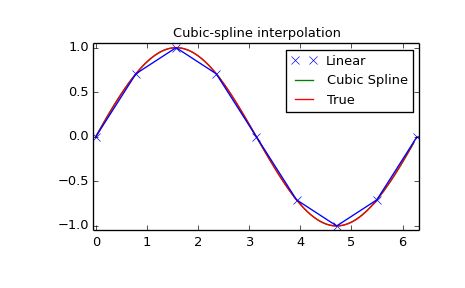
Cubic-spline

import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate

x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
y = np.sin(x)
tck = interpolate.splrep(x, y, s=0)
xnew = np.arange(0,2*np.pi,np.pi/50)
ynew = interpolate.splev(xnew, tck, der=0)

plt.figure()
plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
plt.legend(['Linear', 'Cubic Spline', 'True'])
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('Cubic-spline interpolation')
plt.show()

Derivative of spline

yder = interpolate.splev(xnew, tck, der=1)
plt.figure()
plt.plot(xnew,yder,xnew,np.cos(xnew),'--')
plt.legend(['Cubic Spline', 'True'])
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('Derivative estimation from spline')
plt.show()

Integral of spline

def integ(x, tck, constant=-1):
    x = np.atleast_1d(x)
    out = np.zeros(x.shape, dtype=x.dtype)
    for n in xrange(len(out)):
        out[n] = interpolate.splint(0, x[n], tck)
    out += constant
    return out

yint = integ(xnew, tck)
plt.figure()
plt.plot(xnew, yint, xnew, -np.cos(xnew), '--')
plt.legend(['Cubic Spline', 'True'])
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('Integral estimation from spline')
plt.show()

Roots of spline

print(interpolate.sproot(tck))[ 0.      3.1416]

Parametric spline

t = np.arange(0, 1.1, .1)
x = np.sin(2*np.pi*t)
y = np.cos(2*np.pi*t)
tck,u = interpolate.splprep([x,y], s=0)
unew = np.arange(0, 1.01, 0.01)
out = interpolate.splev(unew, tck)

plt.figure()
plt.plot(x, y, 'x', out[0], out[1], np.sin(2*np.pi*unew), np.cos(2*np.pi*unew), x, y, 'b')
plt.legend(['Linear', 'Cubic Spline', 'True'])
plt.axis([-1.05, 1.05, -1.05, 1.05])
plt.title('Spline of parametrically-defined curve')

Interpolated Univariate Spline

import numpy as np
import matplotlib.pyplot as plt
from scipy import interpolate

x = np.arange(0, 2*np.pi+np.pi/4, 2*np.pi/8)
y = np.sin(x)
s = interpolate.InterpolatedUnivariateSpline(x, y)
xnew = np.arange(0, 2*np.pi, np.pi/50)
ynew = s(xnew)

plt.figure()
plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
plt.legend(['Linear', 'InterpolatedUnivariateSpline', 'True'])
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('InterpolatedUnivariateSpline')
plt.show()

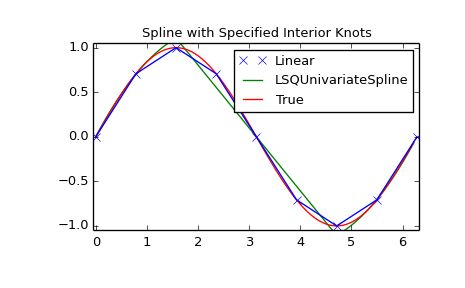
LSQUnivarateSpline with non-uniform knots

t = [np.pi/2-.1, np.pi/2+.1, 3*np.pi/2-.1, 3*np.pi/2+.1]
s = interpolate.LSQUnivariateSpline(x, y, t, k=2)
ynew = s(xnew)

plt.figure()
plt.plot(x, y, 'x', xnew, ynew, xnew, np.sin(xnew), x, y, 'b')
plt.legend(['Linear', 'LSQUnivariateSpline', 'True'])
plt.axis([-0.05, 6.33, -1.05, 1.05])
plt.title('Spline with Specified Interior Knots')
plt.show()

Two-dimensional spline representation: Procedural (bisplrep)

For (smooth) spline-fitting to a two dimensional surface, the functionbisplrep is available. This function takes as required inputs the 1-D arrays x, y, and z which represent points on the surface z=f(x,y).z=f(x,y). The default output is a list[tx,ty,c,kx,ky][tx,ty,c,kx,ky] whose entries represent respectively, the components of the knot positions, the coefficients of the spline, and the order of the spline in each coordinate. It is convenient to hold this list in a single object, tck, so that it can be passed easily to the function bisplev. The keyword, s , can be used to change the amount of smoothing performed on the data while determining the appropriate spline. The default value is s=m−2m‾‾‾√s=m−2m where mm is the number of data points in the x, y, and z vectors. As a result, if no smoothing is desired, then s=0s=0 should be passed tobisplrep .

To evaluate the two-dimensional spline and it’s partial derivatives (up to the order of the spline), the functionbisplev is required. This function takes as the first two arguments two 1-D arrays whose cross-product specifies the domain over which to evaluate the spline. The third argument is the tck list returned from bisplrep. If desired, the fourth and fifth arguments provide the orders of the partial derivative in the xx and yy direction respectively.

It is important to note that two dimensional interpolation should not be used to find the spline representation of images. The algorithm used is not amenable to large numbers of input points. The signal processing toolbox contains more appropriate algorithms for finding the spline representation of an image. The two dimensional interpolation commands are intended for use when interpolating a two dimensional function as shown in the example that follows. This example uses the mgrid command in NumPy which is useful for defining a “mesh-grid” in many dimensions. (See also theogrid command if the full-mesh is not needed). The number of output arguments and the number of dimensions of each argument is determined by the number of indexing objects passed in mgrid.

Define function over sparse 20x20 grid.

import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt

x, y = np.mgrid[-1:1:20j, -1:1:20j]
z = (x+y) * np.exp(-6.0*(x*x+y*y))

plt.figure()
plt.pcolor(x, y, z)
plt.colorbar()
plt.title("Sparsely sampled function.")
plt.show()

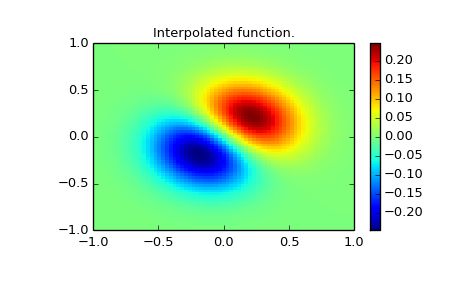
Interpolate function over new 70x70 grid.

xnew, ynew = np.mgrid[-1:1:70j, -1:1:70j]
tck = interpolate.bisplrep(x, y, z, s=0)
znew = interpolate.bisplev(xnew[:,0], ynew[0,:], tck)

plt.figure()
plt.pcolor(xnew, ynew, znew)
plt.colorbar()
plt.title("Interpolated function.")
plt.show()

Two-dimensional spline representation: Object-oriented (BivariateSpline)

The BivariateSpline class is the 2-dimensional analog of theUnivariateSpline class.  It and its subclasses implement the FITPACK functions described above in an object oriented fashion, allowing objects to be instantiated that can be called to compute the spline value by passing in the two coordinates as the two arguments.

Using radial basis functions for smoothing/interpolation

Radial basis functions can be used for smoothing/interpolating scattered data in n-dimensions, but should be used with caution for extrapolation outside of the observed data range.

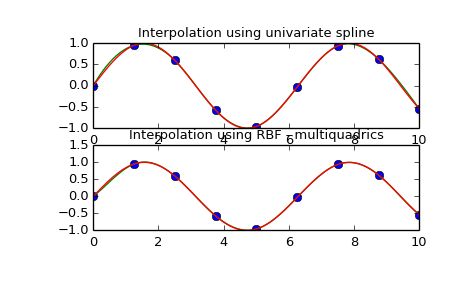
1-d Example

This example compares the usage of the Rbf and UnivariateSpline classes from the scipy.interpolate module.

import numpy as np
from scipy.interpolate import Rbf, InterpolatedUnivariateSpline
import matplotlib.pyplot as plt

# setup data
x = np.linspace(0, 10, 9)
y = np.sin(x)
xi = np.linspace(0, 10, 101)

# use fitpack2 method
ius = InterpolatedUnivariateSpline(x, y)
yi = ius(xi)

plt.subplot(2, 1, 1)
plt.plot(x, y, 'bo')
plt.plot(xi, yi, 'g')
plt.plot(xi, np.sin(xi), 'r')
plt.title('Interpolation using univariate spline')

# use RBF method>>> rbf = Rbf(x, y)
fi = rbf(xi)

plt.subplot(2, 1, 2)
plt.plot(x, y, 'bo')
plt.plot(xi, fi, 'g')
plt.plot(xi, np.sin(xi), 'r')
plt.title('Interpolation using RBF - multiquadrics')
plt.show()

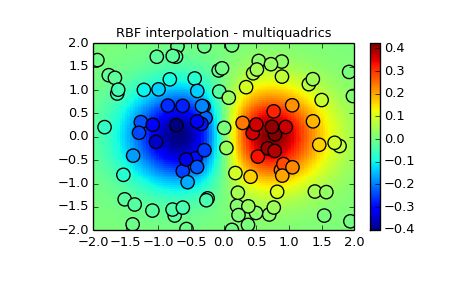
2-d Example

This example shows how to interpolate scattered 2d data.

import numpy as np
import matplotlib.pyplot as plt
from scipy.interpolate import Rbf
from matplotlib import cm

# 2-d tests - setup scattered data
x = np.random.rand(100)*4.0-2.0
y = np.random.rand(100)*4.0-2.0
z = x*np.exp(-x**2-y**2)
ti = np.linspace(-2.0, 2.0, 100)
XI, YI = np.meshgrid(ti, ti)

# use RBF
rbf = Rbf(x, y, z, epsilon=2)
ZI = rbf(XI, YI)

# plot the result
n = plt.normalize(-2., 2.)
plt.subplot(1, 1, 1)
plt.pcolor(XI, YI, ZI, cmap=cm.jet)
plt.scatter(x, y, 100, z, cmap=cm.jet)
plt.title('RBF interpolation - multiquadrics')
plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.colorbar()