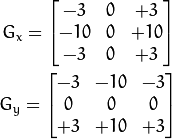首先要了解一下梯度的概念,在高等数学中,对于连续的二维函数f(x,y),其点在(x,y)处的梯度是一个二维列向量
V = [f对x偏导数 f对y偏导数]’
那么梯度的幅值就是
|V| = sqrt(f对x偏导数^2 + f对y偏导数^2)
从而对于离散的二维离散的函数f(i,j),微分往往可以用差分表示,如下式:
| V’| = sqrt([f(i+1,j) - f(i,j)]^2 + [f(i,j+1) - f(i,j)]^2)
在图像处理中,往往将梯度幅值看作是梯度!两者不加以区分。为了方便计算,可以将上述根式近似为绝对值的形式:
| V’| = |f(i+1,j) - f(i,j)| + |f(i+1,j) - f(i,j)|
在实际应用中,往往使用另一种近似梯度-----Robert交叉梯度
| V’| = |f(i+1,j+1) - f(i,j)| + |f(i,j+1) - f(i+1,j)|
常用的两种一阶导数的图像增强算子:
Robert算子:
[-1, 0; 0, 1]:检测接近45度边缘 ----G1
[0, -1; 1, 0]:检测接近-45度边缘 ----G2
最终的robert交叉梯度图像为G = G1 + G2
Sobel算子:
[-1, -2, -1; 0, 0, 0; 1, 2, 1]:对水平边缘有较大响应 -----G1
[-1, 0, 1; -2, 0, 2; -1, 0, 1]:对竖直边缘有较大响应 -----G2
Sobel梯度图像 G = G1 + G2
(注:因为对于图像出来,人们更喜欢使用奇数尺寸的模板,于是sobel算子用得更为普遍)
Sobel算子在openCV中的使用:
cvSobel( const CvArr* scr ,
CvArr* dst ,
int xorder,
int yorder,
int aperture_size = 3);
<!--EndFragment-->
*Xorder,yorder:
X方向,y方向上的导数阶数,通常只用到0,1,最多2
*aperture_size:
扩展 Sobel 核的大小,必须是 1, 3, 5 或 7。 除了尺寸为 1, 其它情况下, aperture_size ×aperture_size 可分离内核将用来计算差分。对 aperture_size=1的情况, 使用 3x1 或 1x3 内核 (不进行高斯平滑操作)。这里有一个特殊变量 CV_SCHARR (=-1),对应 3x3 Scharr 滤波器,可以给出比 3x3 Sobel 滤波更精确的结果。这里的scharr滤波器实际上使用了下图所示的模板,与普通3*3模板不同的是微分权重系数不同
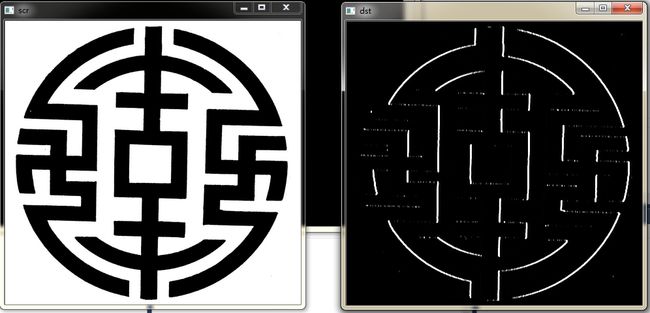
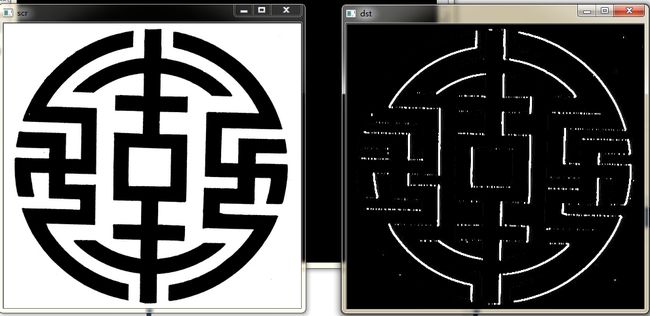
结果比对:
<!--EndFragment-->