近似装箱问题(两种脱机算法实现)
【0】README
0.1) 本文总结于 数据结构与算法分析, 源代码均为原创, 旨在 理解 “近似装箱问题(两种脱机算法实现)” 的idea 并用源代码加以实现;
0.2) 近似装箱问题的两种联机算法 分别是: 首次适合递减算法 和 最佳适合递减算法 , 我们将依次给出源代码实现+算法描述;
0.3)联机算法+脱机算法
- version1)联机装箱问题: 在这种问题中, 必须将每一件物品放入一个箱子后才处理下一件物品;(英语口语考试, 做完上一题,才能进入下一题作答)
- version2)脱机装箱问题:在一个脱机装箱算法中, 我们做任何事情 都需要等到所有的输入数据全被读入后才进行;(一般的考试,你只需要在规定的时间做完题目即可,做题顺序不是我们所关心的)
0.3)不得不提的是: 我的源代码中,桶的容量设为了10,而不是1:原因是 由于 C语言的double类型的精度无法准确表示 小数值(它的有效位数是15~16位),所以,会使得最后的算法结果错误, 当然了对于容量为1的版本,我也写了源代码,参见:https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter10/p274_firstFitDecreaseOne, 有兴趣的朋友,可以down 下来,运行并测试一下;
【1】脱机算法相关
1.0)联机算法的主要问题:在于将大项物品装箱困难, 特别是当他们在输入的晚期出现的时候,
1.1)围绕这个问题的自然方法:将各项物品排序,把最大的物品放在最先,此时我们可以应用首次适合算法或最佳适合算法,分别得到 “首次适合递减算法” 和 ”最佳适合递减算法”;
1.2)看个荔枝(可以产生的最优解):
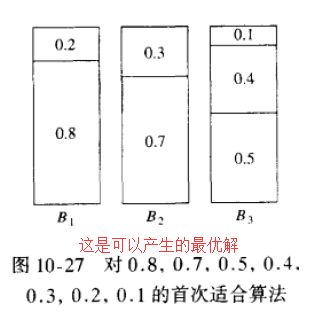
1.3)我们可以证明的结论有(Conclusion):
- C1)如果一种最优装箱法使用M 个箱子, 那么首次适合递减算法使用的箱子数目绝对不超过 (4M+1)/3;
- C2)首先, 所有重量大于1/3 的项将被放入前M个箱子内, 这意味着, 在外加的箱子中所有各项的重量顶多是 1/3;
- C3)在外加的箱子中 , 物品的项数最多是 M-1;
- C4)结合C2 和 C3, 我们发现, 外加的箱子最多可能需要 |(M-1)/3|(不小于(M-1)/3 的最小整数)个;
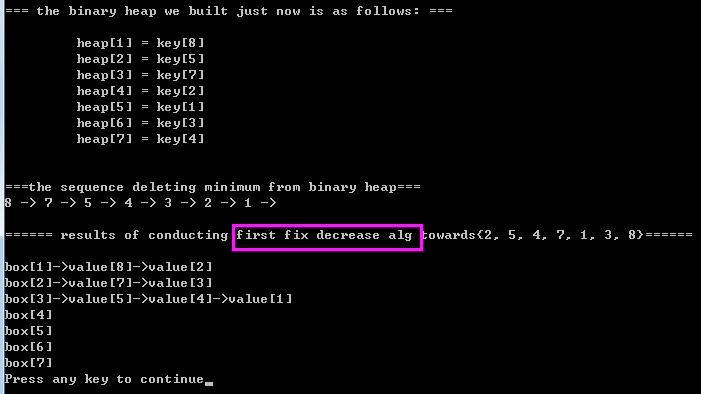
【2】source code + printing results(first fit decrease alg)
2.1)download source code: https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter10/p274_firstFitDecreaseTen
2.2)source code at a glance:(for complete code , please click the given link above)
int main()
{
ElementTypePtr tempBox;
int tempKey;
int key[7] = {2, 5, 4, 7, 1, 3, 8};
int i;
size = 7;
initBox(size);
surplus = buildBasicArray(size, 10); // building surplus array to store surplus value
tempBox = buildSingleElement();
bh = initBinaryHeap(size + 1);
for(i=0; i<size; i++)
{
tempBox->key = key[i];
insertHeap(*tempBox, bh);
}// building binary heap over
printBinaryHeap(bh);
printf("\n");
printf("\n===the sequence deleting minimum from binary heap===\n");
while(!isEmpty(bh))
{
tempKey = deleteMin(bh)->key;
printf("%d -> ", tempKey);
firstFixDecrease(tempKey);
}
printf("\n");
printBox(size);
return 0;
}
void firstFixDecrease(int key)
{
int i;
ElementTypePtr box;
ElementTypePtr temp;
box = buildSingleElement();
box->key = key; // build single box with key over
for(i=0; i<size; i++)
{
if(surplus[i] < key)
continue;
else
break;
}
temp = boxes[i] ;
while(temp->next)
temp = temp->next;
temp->next = box;
surplus[i] -= key;
}【3】source code + printing results(best fit decrease alg)
3.1)download source code: https://github.com/pacosonTang/dataStructure-algorithmAnalysis/tree/master/chapter10/p274_bestFitDecreaseTen
3.2)source code at a glance:(for complete code , please click the given link above)
int main()
{
ElementTypePtr tempBox;
int tempKey;
int key[7] = {2, 5, 4, 7, 1, 3, 8};
int i;
size = 7;
initBox(size);
surplus = buildBasicArray(size, 10); // building surplus array to store surplus value
tempBox = buildSingleElement();
bh = initBinaryHeap(size + 1);
for(i=0; i<size; i++)
{
tempBox->key = key[i];
insertHeap(*tempBox, bh);
}// building binary heap over
printBinaryHeap(bh);
printf("\n");
printf("\n===the sequence deleting minimum from binary heap===\n");
while(!isEmpty(bh))
{
tempKey = deleteMin(bh)->key;
printf("%d -> ", tempKey);
bestFixDecrease(tempKey);
}
printf("\n");
printBox(size);
return 0;
}
void bestFixDecrease(int key)
{
int i;
ElementTypePtr box;
ElementTypePtr temp;
int minimum;
int miniIndex;
box = buildSingleElement();
box->key = key; // build single box with key over
miniIndex = 0;
minimum = 10;
for(i=0; i<size; i++)
{
if(surplus[i] < key)
continue;
if(surplus[i] - key < minimum)
{
minimum = surplus[i] - key;
miniIndex = i;
}
}
temp = boxes[miniIndex] ;
while(temp->next)
temp = temp->next;
temp->next = box;
surplus[miniIndex] -= key;
}