【OpenGL(SharpGL)】支持任意相机可平移缩放的轨迹球实现

【OpenGL(SharpGL)】支持任意相机可平移缩放的轨迹球

（本文PDF版在这里。）

在3D程序中，轨迹球（ArcBall）可以让你只用鼠标来控制模型（旋转），便于观察。在这里（http://www.yakergong.net/nehe/ ）有nehe的轨迹球教程。

本文提供一个本人编写的轨迹球类（ArcBall.cs），它可以直接应用到任何camera下，还可以同时实现缩放和平移。工程源代码在文末。

1. 轨迹球原理

上面是我黑来的两张图，拿来说明轨迹球的原理。

看左边这个，网格代表绘制3D模型的窗口，上面放了个半球，这个球就是轨迹球。假设鼠标在网格上的某点A，过A点作网格所在平面的垂线，与半球相交于点P，P就是A在轨迹球上的投影。鼠标从A1点沿直线移动到A2点，对应着轨迹球上的点P1沿球面移动到了P2。那么，从球心O到P1和P2分别有两个向量OP1和OP2。OP1旋转到了OP2，我们就认为是模型也按照这个方式作同样的旋转。这就是轨迹球的旋转思路。

右边这个图没用上…

2. 轨迹球实现

实现轨迹球，首先要求出鼠标点A1、A2投影到轨迹球上的点P1、P2的坐标，然后计算两个向量A1P1和A2P2之间的夹角以及旋转轴，最后让模型按照求出的夹角和旋转轴，调用glRotate就可以了。

1) 计算投影点

在摄像机上应用轨迹球，才能实现适应任意位置摄像机的ArcBall类。

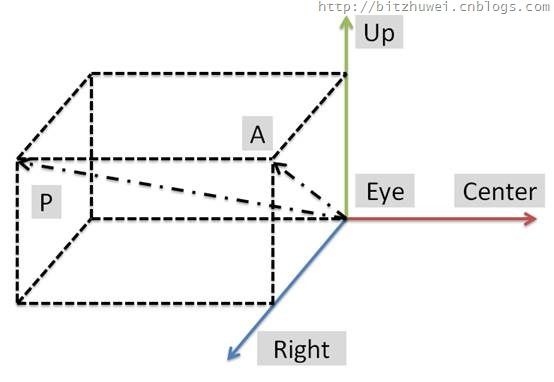
如图所示，红绿蓝三色箭头的交点是摄像机eye的位置，红色箭头指向center的位置，绿色箭头指向up的位置，蓝色箭头指向右侧。

说明：1.Up是可能在蓝色Right箭头的垂面内的任意方向的，这里我们要把它调整为与红色视线垂直的Up，即上图所示的Up。2.绿色和蓝色箭头组成的平面即为程序窗口所在位置，因为Eye就在这里嘛。而且Up指的就是屏幕正上方，Right指的就是屏幕正右方。3.显然轨迹球的半球在图中矩形所在的这一侧，球心就是Eye。

鼠标在Up和Right所在的平面移动，当它位于A点时，投影到轨迹球的点P。现在已知的是Eye、Center、原始Up、A点在屏幕上的坐标、向量Eye-P的长度、向量AP的长度。现在要求P点的坐标，只不过是一个数学问题了。

当然，开始的时候要设置相机位置。

 1         public void SetCamera(float eyex, float eyey, float eyez,
 2             float centerx, float centery, float centerz,
 3             float upx, float upy, float upz)
 4         {
 5             _vectorCenterEye = new Vertex(eyex - centerx, eyey - centery, eyez - centerz);
 6             _vectorCenterEye.Normalize();
 7             _vectorUp = new Vertex(upx, upy, upz);
 8             _vectorRight = _vectorUp.VectorProduct(_vectorCenterEye);
 9             _vectorRight.Normalize();
10             _vectorUp = _vectorCenterEye.VectorProduct(_vectorRight);
11             _vectorUp.Normalize();
12         }

  

根据鼠标在屏幕上的位置投影点的计算方法如下。

 1         private Vertex GetArcBallPosition(int x, int y)
 2         {
 3             var rx = (x - _width / 2) / _length;
 4             var ry = (_height / 2 - y) / _length;
 5             var zz = _radiusRadius - rx * rx - ry * ry;
 6             var rz = (zz > 0 ? Math.Sqrt(zz) : 0);
 7             var result = new Vertex(
 8                 (float)(rx * _vectorRight.X + ry * _vectorUp.X + rz * _vectorCenterEye.X),
 9                 (float)(rx * _vectorRight.Y + ry * _vectorUp.Y + rz * _vectorCenterEye.Y),
10                 (float)(rx * _vectorRight.Z + ry * _vectorUp.Z + rz * _vectorCenterEye.Z)
11                 );
12             return result;
13         }

 这里主要应用了向量的思想，向量(Eye-P) = 向量(Eye-A) + 向量(A-P)。而向量(Eye-A)和向量(A-P)都是可以通过单位长度的Up、Center-Eye和Right向量求得的。

2) 计算夹角和旋转轴

首先，设置鼠标按下事件

1         public void MouseDown(int x, int y)
2         {
3             this._startPosition = GetArcBallPosition(x, y);
4 
5             mouseDownFlag = true;
6         }

 

然后，设置鼠标移动事件。此时P1P2两个点都有了，旋转轴和夹角就都可以计算了。

 1         public void MouseMove(int x, int y)
 2         {
 3             if (mouseDownFlag)
 4             {
 5                 this._endPosition = GetArcBallPosition(x, y);
 6                 var cosAngle = _startPosition.ScalarProduct(_endPosition) / (_startPosition.Magnitude() * _endPosition.Magnitude());
 7                 if (cosAngle > 1) { cosAngle = 1; }
 8                 else if (cosAngle < -1) { cosAngle = -1; }
 9                 var angle = 10 * (float)(Math.Acos(cosAngle) / Math.PI * 180);
10                 System.Threading.Interlocked.Exchange(ref _angle, angle);
11                 _normalVector = _startPosition.VectorProduct(_endPosition);
12                 _startPosition = _endPosition;
13             }
14         }

  

然后，设置鼠标弹起的事件。

1         public void MouseUp(int x, int y)
2         {
3             mouseDownFlag = false;
4         }

 

在使用opengl（sharpgl）绘制的时候，调用

 1         public void TransformMatrix(OpenGL gl)
 2         {
 3             gl.PushMatrix();
 4             gl.LoadIdentity();
 5             gl.Rotate(2 * _angle, _normalVector.X, _normalVector.Y, _normalVector.Z);
 6             System.Threading.Interlocked.Exchange(ref _angle, 0);
 7             gl.MultMatrix(_lastTransform);
 8             gl.GetDouble(Enumerations.GetTarget.ModelviewMatix, _lastTransform);
 9             gl.PopMatrix();
10             gl.Translate(_translateX, _translateY, _translateZ);
11             gl.MultMatrix(_lastTransform);
12             gl.Scale(Scale, Scale, Scale);
13         }

 

3. 额外功能实现

缩放很容易实现，直接设置Scale属性即可。

沿着屏幕上下左右前后地移动，则需要参照着camera的方向动了。

1         public void GoUp(float interval)
2         {
3             this._translateX += this._vectorUp.X * interval;
4             this._translateY += this._vectorUp.Y * interval;
5             this._translateZ += this._vectorUp.Z * interval;
6         }

 

其余方向与此类似，不再浪费篇幅。

工程源代码在此。（http://files.cnblogs.com/bitzhuwei/Arcball6662014-02-07_20-07-00.rar）