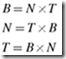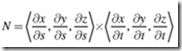《The Cg Tutorial》阅读笔记——凹凸贴图 Bump Mapping
本文为大便一箩筐的原创内容,转载请注明出处,谢谢:http://www.cnblogs.com/dbylk/p/5018103.html
凹凸贴图 Bump Mapping
一、简介
凹凸贴图用于在不增加模型的几何复杂度的情况下模拟几何体表面的复杂细节,从而增加真实感。通过将影响物体光照外观的表面特征存入纹理中,使用凹凸贴图的优点有:
-
在不增加更多几何体的情况下提供更高的视觉复杂度。
-
简化模型的制作。
-
为同一个模型提供不同的表面外观。
二、砖墙法线贴图 The Brick Wall Normal Map
1. 意义
在真实世界中,砖墙是由砂浆和砖块堆砌成的,形成的表面并不平坦。在虚拟世界中构建砖墙时,可以通过为砖墙的每一个凹凸细节都构建多边形并设置表面法线来展现这些细节,但这种方法需要的多边形数目可能是一个天文数字。因此,通常做法是采用法线贴图的方式模拟这些细节。
2. 将凹凸贴图存储为法线贴图
1) 法线贴图
凹凸贴图具有多种不同的形式,接下来会介绍使用表面法线代表物体表面变化的凹凸贴图,这种类型的凹凸贴图通常被称为法线贴图。
2) 法线贴图的存储形式
法线贴图中存储的法线通常为三元单位向量,由于纹理贴图中,色彩的取值范围会被限制在[0.0f, 1.0f]之间,而法线向量的取值范围在[-1.0f, 1.0f]之间,所以通常会采用下面的公式进行转换:
ColorComponent = 0.5 * NormalComponent + 0.5
NormalComponent = 2 * (ColorComponent - 0.5)
注:现代GPU已经支持有符号纹理贴图,是否采用这种转换取决于项目需要。
3) 通过高度场生成法线贴图 Generating Normal Maps from Height Fields
高度场纹理使用单个字节存储了每一个纹理像素(texel)的高度。将高度场转化为法线贴图的步骤如下:
A. 取目标像素点高度Hg,目标相邻右侧像素点高度Hr,目标相邻上侧像素点高度Ha
B. 计算目标像素点至右侧像素点的方向向量(1, 0, Hr - Hg)和目标像素点至上侧像素点的方向向量(0, 1, Ha - Hg)
C. 计算上一步中两个方向向量的叉积,并标准化。公式如下:
Normal = (Hg - Ha, Hg - Hr, 1) / sqrt((Hg - Ha)2 + (Hg - Hr)2 + 1)
D. 对获取的法线单位向量进行压缩处理(将各分量取值范围从[-1.0f, 1.0f]压缩至[0.0f, 1.0f]之间)
由于砖墙的大体为一个平面,因此它的大多数法线单位向量为(0, 0, 1),所以它的法线贴图主要呈蓝色。
- 构建标准化立方贴图
一般情况下,向量标准化的计算公式为:
NormalizeV = V / sqrt(dot(V, V))
而在NVidia的CG着色器语言标准库中,包含了一个名为标准化单位向量的规范例程,它通过将预先计算好的标准化结果存储在立方贴图中的方式获取向量的标准化结果。而这种方式比使用公式进行计算要快得多。
3. 对复杂几何体使用凹凸贴图
1) 凹凸贴图的局限性
在上面的例子中,描述了凹凸贴图在一个简单的例子中如何使用:砖墙的表面是平坦、均匀且 正常的,纹理坐标与分配到的顶点位置是一个简单统一的线性映射。然而,在实际情况中,任意几何体的纹理坐标(s, t)与对象空间的位置坐标(x, y)往往不是简单的线性关系,物体表面法线的单位向量多数情况下也不是(0, 0, 1),这种情况下直接对应会产生错误的结果。
2) 对象空间凹凸贴图
为了纠正上述错误,一种解决方案就是使法线贴图的中存储的法线方向与对象空间保持一致。
【优点】不需要额外的计算
【缺点】法线贴图不能在不同模型之间共用
对有动画的模型来说,每个动作都需要独立的法线贴图
3) 纹理空间凹凸贴图
将光线向量和半角向量转换到纹理空间,从而计算光照。
【优点】可以多个对象或在对象动画中共享法线贴图
【缺点】需要对每个顶点执行两次额外的向量变换
三、砖块地板法线贴图 The Brick Floor Normal Map
砖块地板在砖墙的基础上发生了旋转,表面法线由(0, 0, 1)变为了(0, 1, 0)。为了与砖墙共用同一张法线贴图,我们需要使用旋转矩阵对光线的方向向量进行旋转。
表示三维向量旋转的变换矩阵具有如下性质:
- 每行 / 每列都是一个单位向量
- 每列向量都与其他两列向量正交
我们分别称旋转矩阵的三个列向量为切线Tangent、副法线Binormal与法线Normal。
知道其中任意两列向量,便可根据正交性质求得第三列。
因此在着色器中,我们只需要为每个顶点定义切线和法线属性,就可以通过叉积公式求得顶点的纹理空间转换矩阵。
四、环面体法线贴图 Bump Mapping a Torus
1. 环面体的数学表达
对环面体使用凹凸贴图比在上一章节中描述的情况更加复杂,但又比对任意多边形使用凹凸贴图简单许多。
下面是环面体的顶点坐标的参数方程(以坐标轴原点为中心,放置于xOy平面):
x = (M + N · cos(2πt) · cos(2πs)
y = (M + N · cos(2πt) · cos(2πs)
z = N · sin(2πt)
- M为圆环中心到管道圆心的半径
- N为管道的半径
- (s, t)∈[0, 1],s表示了顶点在圆环上的相对位置,t表示了顶点在管道上的相对位置
2. 计算光向量转换至环面体纹理空间的旋转矩阵
创建旋转矩阵需要用到环面体参数方程的偏导数:
我们把“包含s或t的偏导数”组成的三维向量称为逆梯度,因为它类似于每个分量的常规地图的倒数。一个逆梯度表示了一个单参数变量在物体表面位置的瞬时方向与变化幅度。
我们可以用逆梯度来构建一个表面局部坐标系Surface-Local Coordinate System,创建一个3D坐标系需要两个正交的向量。对表面局部坐标系来说,表面法线向量非常关键,我们可以通过计算两个不重合的逆梯度来获取法线向量N。
再选择其中一个逆梯度作为切线,就可以构建一个表面局部坐标系了。
综上所述,环面体的旋转矩阵为:
其中,向量上方的∧符号表示标准化向量。
五、纹理多边形网格凹凸贴图 Bump Mapping Textured Polygonal Meshes
1. 研究单个三角形 Examining a Single Triangle
上图是一个外星人头部的线框模型,它展示了同一个三角形三次:
- 最左边:处于2D高度场纹理中
- 最右边:处于3D对象空间中
- 最中间:处于使用凹凸贴图渲染的图像结果中
其中,三角形的每个顶点都对应了一个三维对象空间坐标与二维纹理坐标,它们共同组成了一个五维坐标,因此,我们可以把一个三角形描述如下:
V0 = (x0, y0, z0, s0, t0)
V1 = (x1, y1, z1, s1, t1)
V2 = (x2, y2, z2, s2, t2)
由于这些坐标处于同一个三角形所在的平面,所以可以用推导出x、y、z分别与s、t有关的平面方程:
A0x + B0s + C0t + D0 = 0
A1x + B1s + C1t + D1 = 0
A2x + B2s + C2t + D2 = 0
对上面每个等式来说,你都能通过三角形的三个五维顶点坐标计算出A、B、C、D的值。以第一个等式为例:
重写平面方程,即可得到使用s、t表示x、y、z的等式:
x = (-B0s - C0t - D0) / A0
y = (-B1s - C1t - D1) / A1
z = (-B2s - C2t - D2) / A2
上述方程为我们提供了使用纹理坐标获取对应三维对象空间坐标的途径,与环面体类似,我们可以通过逆梯度求得旋转矩阵:
注:如果模型提供了顶点法线,则优先使用模型提供的顶点法线。
2. 注意事项
1) 纹理空间与对象空间的正交性
使用上述公式计算逆梯度时,需要保证s与t的逆梯度是正交的。实际项目中,美术往往会使s与t的逆梯度正交,以避免纹理贴图倾斜。
2) 警惕纹理空间中面积为零的三角形
若三角形在纹理空间中面积为零或近似为零(可能在对象空间中仍有面积),将会逆梯度无法正确求值,从而产生不正确的光照效果,因此在使用凹凸贴图时,美术需要避免创建这样的三角形。
3) 纹理空间中的负面积三角形
由于很多模型是对称的,美术可以只绘制一半纹理,将纹理同时通过正向和反向映射到对称的网格中,这种方式应当在凹凸贴图中避免出现,否则会导致凹凸贴图在反向映射的部分效果不正确。
4) 凹凸贴图的纹理坐标非均匀拉伸
不均匀的拉伸可能会导致高度场转化而成的法线贴图不正确。