机器学习公开课笔记(8):k-means聚类和PCA降维
K-Means算法
非监督式学习对一组无标签的数据试图发现其内在的结构,主要用途包括:
- 市场划分(Market Segmentation)
- 社交网络分析(Social Network Analysis)
- 管理计算机集群(Organize Computer Clusters)
- 天文学数据分析(Astronomical Data Analysis)
K-Means算法属于非监督式学习的一种,算法的输入是:训练数据集$\{x^{(1)},x^{(2)},\ldots, x^{(m)}\}$(其中$x^{(i)}\in R^{n}$)和聚类数量$K$(将数据划分为$K$类);算法输出是$K$个聚类中心$\mu_1, \mu_2, \ldots, \mu_K$和每个数据点$x^{(i)}$所在的分类。
K-Means算法步骤
- 随机初始化$K$个聚类中心(cluster centroid) $\mu_1, \mu_2, \ldots, \mu_K$
- Cluster Assignment: 对于每个数据点$x^{(i)}$,寻找离它最近的聚类中心,将其归入该类;即$c^{(i)}=\min\limits_k||x^{(i)}-\mu_k||^2$,其中$c^{(i)}$表示$x^{(i)}$所在的类
- Move Centroid: 更新聚类中心$u_k$的值为所有属于类$k$的数据点的平均值
- 重复2、3步直到收敛或者达到最大迭代次数
K-Means算法的优化目标
用$\mu_{c^{(i)}}$表示第$i$个数据点$x^{(i)}$所在类的中心,则K-Means优化的代价函数为$$J(c^{(1)},\ldots,c^{(m)},\mu_1,\ldots,\mu_K)=\frac{1}{m}\sum\limits_{i=1}^{m}||x^{(i)}-\mu_{c^{(i)}}||^2$$希望找到最优参数使得该函数最小化,即$$\min\limits_{\substack{c^{(1)},\ldots,c^{(m)} \\ \mu_1,\ldots,\mu_K}}J(c^{(1)},\ldots,c^{(m)},\mu_1,\ldots,\mu_K)$$
需要注意的问题
- 随机初始化:常用的初始化方法是,从训练数据点中随机选择$K$($K < m$)个数据点,作为初始的聚类中心$\mu_1, \mu_2, \ldots, \mu_K$
- 局部最优:算法聚类的性能与初始聚类中心的选择有关,为避免陷入局部最优(如图2所示),应该运行多次(50次)取使得$J$最小的结果
- $K$值选择:Elbow方法,绘制$J$随$K$的变化曲线,选择下降速度突然变慢的转折点作为K值;对于转折不明显的曲线,可根据K-Means算法后续的目标进行选择。
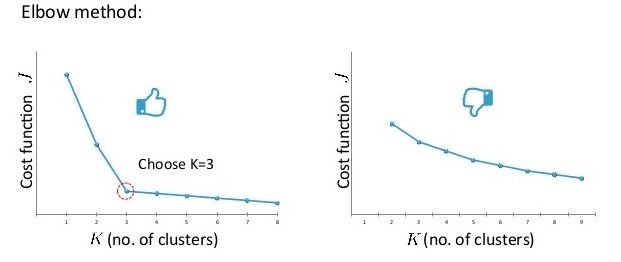 图3 用Elbow方法选择K值的情况(左)和Elbow法不适用的情况(右)
图3 用Elbow方法选择K值的情况(左)和Elbow法不适用的情况(右)
PCA降维算法
动机
数据压缩:将高维数据(n维)压缩为低维数据(k维)
数据可视化:将数据压缩到2维/3维方便可视化
PCA问题形式化
如果需要将二维数据点,压缩为一维数据点,我们需要找到一个方向,使得数据点到这个方向上投射时的误差最小(即点到该直线的距离最小);更一般地,如果需要将$n$维的数据点压缩到$k$维,我们需要找到$k$个新的方向$u^{(1)}, u^{(2)}, \ldots, u^{(k)}$使得数据点投射到每个方向$u^{(i)}$时的误差最小。

图4 PCA实例,将2维数据点压缩为1维数据点,找到新的方向$u_1$,使得投射误差(图中的垂线距离如$x^i$到${\widetilde x}^i$)最小
注意:PCA和线性回归的区别,PCA是保证投射的误差(图5右的黄线)最小,而线性回归是保证沿$y$方向的误差(图5左的黄线)最小.
PCA算法步骤
1. 数据预处理:mean normalization:$\mu_j = \frac{1}{m}\sum\limits_{i=1}^{m}x_j^{(i)}, x_j^{(i)}=x_j-\mu_j$;feature scaling:(可选,不同特征范围差距过大时需要) , $x_j^{(i)}=\frac{x^{(i)}-\mu_j}{\sigma_j}$
2. 计算协方差矩阵(Convariance Matrix) $$\Sigma=\frac{1}{m}\sum\limits_{i=1}^{m}x^{(i)}(x^{(i)})^T \quad \text{or} \quad \Sigma = \frac{1}{m}X^TX$$
3. 计算协方差矩阵$\Sigma$的特征向量 [U, S, V] = svd(Sigma)
4. 选择U矩阵的前k个列向量作为k个主元方向,形成矩阵$U_{reduce}$
5. 对于每个原始数据点$x$($x\in R^n$),其降维后的数据点$z$($z \in R^k$)为 $z=U_{reduce}^T x$
应用PCA
重构数据:对于降维后k维数据点z,将其恢复n维后的近似点为 $x_{apporx}(\approx x)=U_{reduce}z$
选择k值
- 平均投射误差(Average square projection error):$\frac{1}{m}\sum\limits_{i=1}^{m}||x^{(i)}-x^{(i)}_{approx}||^2$
- total variation: $\frac{1}{m}\sum\limits_{i=1}^{m}||x^{(i)}||^2$
- 选择最小的k值使得 $\frac{\frac{1}{m}\sum\limits_{i=1}^{m}||x^{(i)}-x^{(i)}_{approx}||^2}{\frac{1}{m}\sum\limits_{i=1}^{m}||x^{(i)}||^2} \leq 0.01(0.05)$,也可以使用SVD分解后的S矩阵进行选择 $1-\frac{\sum\limits_{i=1}^{k}S_{ii}}{\sum\limits_{i=1}^{n}S_{ii}}\leq 0.01(0.05)$
应用PCA的建议
- 用于加速监督式学习:(1) 对于带标签的数据,去掉标签后进行PCA数据降维,(2)使用降维后的数据进行模型训练,(3) 对于新的数据点,先PCA降维得到降维后数据,带入模型获得预测值。注:应仅用训练集数据进行PCA降维获取映射$x^{(i)}\rightarrow z^{(i)}$,然后将该映射(PCA选择的主元矩阵$U_reduce$)应用到验证集和测试集
- 不要用PCA阻止过拟合,用regularization。
- 在使用PCA之前,先用原始数据进行模型训练,如果不行,再考虑使用PCA;而不要上来直接使用PCA。
参考文献
[1] Andrew Ng Coursera 公开课第八周
[2] 漫谈Clustering:k-means. http://blog.pluskid.org/?p=17
[3] k-means clustering in a GIF. http://www.statsblogs.com/2014/02/18/k-means-clustering-in-a-gif/
[4] Wikipedia: Principal component analysis. https://en.wikipedia.org/wiki/Principal_component_analysis
[5] Explained Visually: Principal component analysis http://setosa.io/ev/principal-component-analysis/


