Unity3D - 详解Quaternion类(二)
OK,不做引子了,接上篇Unity3D - 详解Quaternion类(一)走起!
四、Quaternion类静态方法
Quaternion中的静态方法有9个即:Angle方法、Dot方法、Euler方法、FromToRotation方法、Inverse方法、Lerp方法、LookRotation方法、RotateToWards方法和Slerp方法。关于静态的方法的使用就是直接用类名调用其静态方法,例如Quaternion.Angle(q1,q2);下面对这些静态方法做下分析。
1、Angle方法
1.1 函数原型
public static float Angle(Quaternion a,Quaternion b);
该方法可以计算两个旋转状态a达到b时需要旋转的最小夹角。
1.2 实例演示
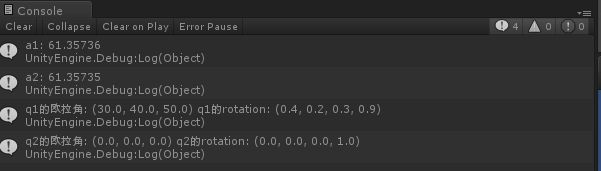
using UnityEngine; using System.Collections; public class Angle_ts : MonoBehaviour { // Use this for initialization void Start () { Quaternion q1 = Quaternion.identity; Quaternion q2 = Quaternion.identity; q1.eulerAngles = new Vector3(30.0f, 40.0f, 50.0f); float a1 = Quaternion.Angle(q1, q2); float a2 = 0.0f; Vector3 v = Vector3.zero; q1.ToAngleAxis(out a2,out v); Debug.Log("a1: " + a1); Debug.Log("a2: " + a2); Debug.Log("q1的欧拉角: " + q1.eulerAngles + " q1的rotation: " + q1); Debug.Log("q2的欧拉角: " + q2.eulerAngles + " q2的rotation: " + q2); } // Update is called once per frame void Update () { } }
运行结果
从输出结果可以看出a1和a2的值相等,即Angle的返回值是两个Quaternion实例转换的最小夹角。
2、Dot方法-点乘
2.1 函数原型
public static float Dot(Quaternion a,Quaternion b);
该方法可以根据点乘的结果,判断a和b对应欧拉角的关系。
例如有两个Quaternion实例q1(x1,y1,z1,w1)和q2(x2,y2,z2,w2),则float f = Quaternion.Dot(q1,q2);即f = x1*x2+y1*y2+z1*z2+w1*w2,结果值f的范围为[-1,1]。
当f=+(-)1时,q1和q2对应的欧拉角是相等的,即旋转状态是一致的。特别地,当f = -1时,说明其中一个rotation比另外一个rotation多旋转了360°。
2.2 实例演示
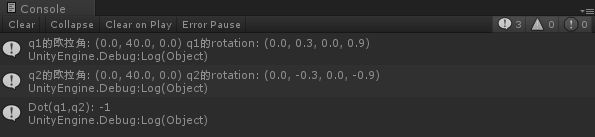
using UnityEngine; using System.Collections; public class Dot_ts : MonoBehaviour { public Transform A, B; Quaternion q1 = Quaternion.identity; Quaternion q2 = Quaternion.identity; // Use this for initialization void Start () { A.eulerAngles = new Vector3(0.0f, 40.0f, 0.0f); B.eulerAngles = new Vector3(0.0f, 360.0f + 40.0f, 0.0f); q1 = A.rotation; q2 = B.rotation; float f = Quaternion.Dot(q1, q2); Debug.Log("q1的欧拉角: " + q1.eulerAngles + " q1的rotation: " + q1); Debug.Log("q2的欧拉角: " + q2.eulerAngles + " q2的rotation: " + q2); Debug.Log("Dot(q1,q2): " + f); } // Update is called once per frame void Update () { } }
运行输出
从输出结果可以证明q1和q2的欧拉角相等,但是rotation值却是相反的,也说明当Dot的返回值为-1时,两个参数的角度相差360°。
3、Euler方法
3.1 函数原型
public static Quaternion Euler(Vector3 euler); public static Quaternion Euler(float x,float y,float z);
该方法用于返回欧拉角Vector3(ex,ey,ez)对应的四元数Quaternion q(qx,qy,qz,qw)。其对应关系如下:
已知PIover180 = 3.141592/180 = 0.0174532925f是计算机图形学中的一个常亮,其变换过程如下:
ex = ex * PIover180 / 2.0f; ey = ey * PIover180 / 2.0f; ez = ez * PIover180 / 2.0f; qx = Mathf.Sin(ex) * Mathf.Cos(ey) * Mathf.Cos(ez) + Mathf.Cos(ex) * Mathf.Sin(ey) * Mathf.Sin(ez); qy = Mathf.Cos(ex) * Mathf.Sin(ey) * Mathf.Cos(ez) - Mathf.Sin(ex) * Mathf.Cos(ey) * Mathf.Sin(ez); qz = Mathf.Cos(ex) * Mathf.Cos(ey) * Mathf.Sin(ez) - Mathf.Sin(ex) * Mathf.Sin(ey) * Mathf.Cos(ez); qw = Mathf.Cos(ex) * Mathf.Cos(ey) * Mathf.Cos(ez) + Mathf.Sin(ex) * Mathf.Sin(ey) * Mathf.Sin(ez);
3.2 验证变换过程
using UnityEngine; using System.Collections; public class Euler_ts : MonoBehaviour { public float ex, ey, ez; float qx, qy, qz,qw; float PIover180 = 0.0174532925f; Quaternion q = Quaternion.identity; Vector3 euler; void OnGUI() { if(GUI.Button(new Rect(10.0f,10.0f,100.0f,45.0f),"计算")) { euler = new Vector3(ex,ey,ez); Debug.Log("欧拉角Euler(ex,ey,ez): " + euler); q = Quaternion.Euler(ex, ey, ez); Debug.Log("对应的四元数为: " + q); Debug.Log("q.x: " + q.x + " q.y: " + q.y + " q.z: " + q.z + " q.w: " + q.w); //验证算法 ex = ex * PIover180 / 2.0f; ey = ey * PIover180 / 2.0f; ez = ez * PIover180 / 2.0f; qx = Mathf.Sin(ex) * Mathf.Cos(ey) * Mathf.Cos(ez) + Mathf.Cos(ex) * Mathf.Sin(ey) * Mathf.Sin(ez); qy = Mathf.Cos(ex) * Mathf.Sin(ey) * Mathf.Cos(ez) - Mathf.Sin(ex) * Mathf.Cos(ey) * Mathf.Sin(ez); qz = Mathf.Cos(ex) * Mathf.Cos(ey) * Mathf.Sin(ez) - Mathf.Sin(ex) * Mathf.Sin(ey) * Mathf.Cos(ez); qw = Mathf.Cos(ex) * Mathf.Cos(ey) * Mathf.Cos(ez) + Mathf.Sin(ex) * Mathf.Sin(ey) * Mathf.Sin(ez); Debug.Log("qx: " + qx + " qy: " + qy + " qz: " + qz + " qw: " + qw); } } }
运行结果
从输出结果可以证明该公式是正确,另外转换后的四元数直接输出的话,如下:
q = Quaternion.Euler(ex, ey, ez); Debug.Log("对应的四元数为: " + q);
输出值是做了四舍五入处理的。
4、FromToRotation方法
函数原型
public static Quaternion FromToRotation(Vector3 fromDirection,Vector3 ToDirection);
在前面介绍了SetFromToRotation实例方法,它们的功能都是一样的只不过用法稍有不同。使用FromToRotation类静态方法,需要直接使用类名进行调用,如Quaternion.FromToRotation(v1,v2);
在此就不做演示了!
5、Inverse方法
5.1 函数原型
public static Quaternion Inverse(Quaternion rotation);
该方法可以返回参数rotation的逆向Quaternion值。
例如rotation(x,y,z,w),那么Quaternion.Inverse(rotation) = (-x,-y,-z,w)。假设rotation的欧拉角为(a,b,c),则transform.rotation = Quaternion.Inverse(rotation)相当于transform依次绕自身坐标系的z轴、x轴和y轴分别旋转-c°、-a°和-z°。由于是在局部坐标系内的变换,最后transform的欧拉角的各个分量值并不一定等于-a、-b或-c。
5.2 实例演示
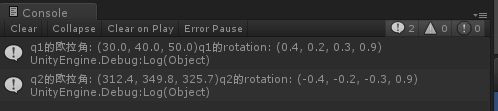
using UnityEngine; using System.Collections; public class Invers_ts : MonoBehaviour { public Transform A, B; // Use this for initialization void Start () { Quaternion q1 = Quaternion.identity; Quaternion q2 = Quaternion.identity; q1.eulerAngles = new Vector3(30.0f,40.0f,50.0f); q2 = Quaternion.Inverse(q1); A.rotation = q1; B.rotation = q2; Debug.Log("q1的欧拉角: " + q1.eulerAngles + "q1的rotation: " + q1); Debug.Log("q2的欧拉角: " + q2.eulerAngles + "q2的rotation: " + q2); } // Update is called once per frame void Update () { } }
运行截图
6、Lerp和Slerp方法
6.1 函数原型
public static Quaternion Lerp(Quaternion form, Quaternion to,float t); public static Quaternion Slerp(Quaternion form, Quaternion to,float t);
两种方法的作用都是返回从form到to的插值。当参数t<=0时返回值为from,当参数t>=1时返回值为to。其中Lerp是线性差值,而Slerp是球面插值。
6.2 实例演示
using UnityEngine; using System.Collections; public class LerpAndSlerp_ts : MonoBehaviour { public Transform A, B, C,D; float speed = 0.2f; float total = 0.0f; // Use this for initialization void Start () { } // Update is called once per frame void Update () { total += Time.deltaTime * speed; if(total >= 1.0f) total = 1.0f; C.rotation = Quaternion.Lerp(A.rotation, B.rotation, total); D.rotation = Quaternion.Lerp(A.rotation, B.rotation, total); //C.rotation = Quaternion.Lerp(A.rotation, B.rotation, Time.deltaTime * speed); //D.rotation = Quaternion.Lerp(A.rotation, B.rotation, Time.deltaTime * speed); } }
7、RotateTowards方法
7.1 函数原型
public static Quaternion RotateTowards(Quaternion from, Quaternion to, float maxDegreesDelta);
该方法也是一个插值方法,即从返回参数from到to的插值,且返回值的最大角度不超过maxDegreesDelta。maxDegreesDelta是角度值,不是插值系数,当maxDegreesDelta < 0时,将进行逆向插值即从to到from的方向进行插值计算。
7.2 实例演示
using UnityEngine; using System.Collections; public class RotateToWards_ts : MonoBehaviour { public Transform A, B, C; float speed = 10.0f; float total = 0.0f; // Use this for initialization void Start() { } // Update is called once per frame void Update() { total += Time.deltaTime * speed; if (total >= 1.0f) total = 1.0f; C.rotation = Quaternion.RotateTowards(A.rotation, B.rotation, Time.time * speed - 40.0f); Debug.Log("C与A的欧拉角的插值: " + (C.eulerAngles - A.eulerAngles) + "maxDegreesDelta: " + (Time.time * speed - 40.0f)); } }
运行截图
8、LookRotation方法
函数原型
public static Quaternion LookRotation(Vector3 forward); public static Quaternion LookRotation(Vector3 forward,Vector3 upwards);
参数forward为返回Quaternion实例的forward朝向。该方法和前面讲到的SetLookRotation实例方法的功能是一样的,故不多做阐述了。
五、Quaternion类运算符
Quaternion类涉及到两个Quaternion对象相乘和Quaternion对象与Vector3对象相乘,那么就必须重载"*"运算符。
1、函数原型
public static Quaternion operator *(Quaternion lhs, Quaternion rhs); public static Vector3 operator *(Quaternion rotation, Vector3 point);
2、两个Quaternion对象相乘
对于两个Quaternion对象相乘主要用于自身旋转变换,例如:
B.rotation *= A.rotation;
- B会绕着B的局部坐标系的z、x、y轴按照先绕z轴再绕x轴最后绕y轴的旋转次序,分别旋转A.eulerAngles.z度、A.eulerAngles.x度、和A.eulerAngles.y度。由于是绕着局部坐标系进行旋转,所以当绕着其中一个轴进行旋转时,可能会影响其余两个坐标轴方向的欧拉角(除非其余两轴的欧拉角都为0才不会受到影响)。
- 假如A的欧拉角为aEuler(ax,ay,az),则沿着B的初始局部坐标系的aEuler方向向下看B在绕着aEuler顺时针旋转。B的旋转状况还受到其初始状态的影响。
2.1 实例演示
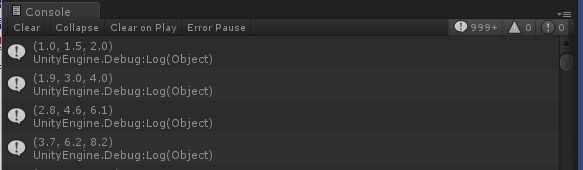
using UnityEngine; using System.Collections; public class Multiply1_ts : MonoBehaviour { public Transform A, B; // Use this for initialization void Start () { A.eulerAngles = new Vector3(1.0f, 1.5f, 2.0f); } // Update is called once per frame void Update () { B.rotation *= A.rotation; Debug.Log(B.eulerAngles); } }
运行截图
2.2 分析
B绕着其自身坐标系的Vector3(1.0f,1.5f,2.0f)方向旋转。虽然每次都绕着这个轴向旋转的角度相同,但角度的旋转在3个坐标轴的值都不为零,三个轴的旋转会相互影响,所以B的欧拉角的各个分量的每次递增是不固定的。
3、Quaternion对象与Vector3对象
对于Quaternion对象与Vector3对象相乘主要用于自身移动变换,例如
transform.position += tansform.rotation * A;
其中A为Vector3的对象。transform对应的对象会沿着自身坐标系中向量A的方向移动A的模长的距离。transform.rotation与A相乘可以确定移动的方向和距离。
3.1 实例演示
using UnityEngine; using System.Collections; public class Multiply2_ts : MonoBehaviour { public Transform A; float speed = 0.1f; // Use this for initialization void Start () { A.position = Vector3.zero; A.eulerAngles = new Vector3(0.0f, 45.0f, 0.0f); } // Update is called once per frame void Update () { A.position += A.rotation * (Vector3.forward * speed); Debug.Log(A.position); } }
运行截图
4、两个Quaternion对象相乘与Quaternion对象与Vector3对象相乘的异同
- 设A为两个两个Quaternion对象相乘的结果。B为Quaternion对象与Vector3对象相乘的结果。其中A为Quaternion类型,B为Vector3类型。
- A与B的相同之处是它们都通过自身坐标系的“相乘”方式来实现在世界坐标系中的变换。
- A主要用来实现transform绕自身坐标系的某个轴旋转,B主要用来实现transform沿着自身坐标系的某个方向移动。
- 必须遵守Quaternion对象*Vector3对象的形式,不可以颠倒顺序。
- 由于它们都是相对于自身坐标系进行的旋转或移动,所以当自身坐标系的轴向和世界坐标系的轴向不一致时,它们绕着自身坐标系中的某个轴向的变动都会影响到物体在世界坐标系中各个坐标轴的变动。
--------------------------------------------------------------------------------------------------------至此完结!-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------