剑指Offer面试题：32.数字在排序数组中出现的次数

一、题目：数字在排序数组中出现的次数

题目：统计一个数字在排序数组中出现的次数。例如输入排序数组{1,2,3,3,3,3,4,5}和数字3，由于3在这个数组中出现了4次，因此输出4。

二、解题思路

2.1 直接运用二分查找

　　既然输入的数组是排序的，那么我们很自然地就能想到用二分查找算法。在题目给出的例子中，我们可以先用二分查找算法找到一个3。由于3可能出现多次，因此我们找到的3的左右两边可能都有3，于是我们在找到的3的左右两边顺序扫描，分别找出第一个3和最后一个3。因为要查找的数字在长度为n的数组中有可能出现O(n)次，所以顺序扫描的时间复杂度是O(n)。因此这种算法的效率和直接从头到尾顺序扫描整个数组统计3出现的次数的方法是一样的。

2.2 改进运用二分查找

　　接下来我们思考如何更好地利用二分查找算法。假设我们是统计数字k在排序数组中出现的次数。在前面的算法中时间主要消耗在如何确定重复出现的数字的第一个k和最后一个k的位置上，有没有可能用二分查找算法直接找到第一个k及最后一个k呢？

　　我们先分析如何用二分查找算法在数组中找到第一个k。二分查找算法总是先拿数组中间的数字和k作比较。如果中间的数字比k大，那么k只有可能出现在数组的前半段，下一轮我们只在数组的前半段查找就可以了。如果中间的数字比k小，那么k只有可能出现在数组的后半段，下一轮我们只在数组的后半段查找就可以了。如果中间的数字和k相等呢？我们先判断这个数字是不是第一个k。如果位于中间数字的前面一个数字不是k，此时中间的数字刚好就是第一个k。如果中间数字的前面一个数字也是k，也就是说第一个k肯定在数组的前半段，下一轮我们仍然需要在数组的前半段查找。

　　（1）GetFirstK：找到数组中第一个k的下标。如果数组中不存在k，返回-1

    private static int GetFirstK(int[] data, int k, int start, int end)
    {
        if (start > end)
        {
            return -1;
        }

        int middIndex = (start + end) / 2;
        int middData = data[middIndex];

        if (middData == k)
        {
            if ((middIndex > 0 && data[middIndex - 1] != k) || middIndex == 0)
            {
                return middIndex;
            }
            else
            {
                end = middIndex - 1;
            }
        }
        else if (middData > k)
        {
            end = middIndex - 1;
        }
        else
        {
            start = middIndex + 1;
        }

        return GetFirstK(data, k, start, end);
    }

　　（2）GetLastK：找到数组中最后一个k的下标。如果数组中不存在k，返回-1

    private static int GetLastK(int[] data, int k, int start, int end)
    {
        if (start > end)
        {
            return -1;
        }

        int middIndex = (start + end) / 2;
        int middData = data[middIndex];

        if (middData == k)
        {
            if ((middIndex < data.Length - 1 && data[middIndex + 1] != k) || middIndex == end)
            {
                return middIndex;
            }
            else
            {
                start = middIndex + 1;
            }
        }
        else if (middData > k)
        {
            end = middIndex - 1;
        }
        else
        {
            start = middIndex + 1;
        }

        return GetLastK(data, k, start, end);
    }

　　（3）GetNumberOfK：找到数组中第一个和最后一个k的下标进行减法运算得到最终结果

    public static int GetNumberOfK(int[] data, int k)
    {
        int number = 0;
        if (data != null && data.Length > 0)
        {
            int first = GetFirstK(data, k, 0, data.Length - 1);
            int last = GetLastK(data, k, 0, data.Length - 1);

            if (first > -1 && last > -1)
            {
                number = last - first + 1;
            }
        }
        return number;
    }

三、单元测试

3.1 测试用例

    // 查找的数字出现在数组的中间
    [TestMethod]
    public void GetNumberTest1()
    {
        int[] data = { 1, 2, 3, 3, 3, 3, 4, 5 };
        int actual = NumberOfKHelper.GetNumberOfK(data, 3);
        Assert.AreEqual(actual, 4);
    }

    // 查找的数组出现在数组的开头
    [TestMethod]
    public void GetNumberTest2()
    {
        int[] data = { 3, 3, 3, 3, 4, 5 };
        int actual = NumberOfKHelper.GetNumberOfK(data, 3);
        Assert.AreEqual(actual, 4);
    }

    // 查找的数组出现在数组的结尾
    [TestMethod]
    public void GetNumberTest3()
    {
        int[] data = { 1, 2, 3, 3, 3, 3 };
        int actual = NumberOfKHelper.GetNumberOfK(data, 3);
        Assert.AreEqual(actual, 4);
    }

    // 查找的数字不存在
    [TestMethod]
    public void GetNumberTest4()
    {
        int[] data = { 1, 3, 3, 3, 3, 4, 5 };
        int actual = NumberOfKHelper.GetNumberOfK(data, 2);
        Assert.AreEqual(actual, 0);
    }

    // 查找的数字比第一个数字还小，不存在
    [TestMethod]
    public void GetNumberTest5()
    {
        int[] data = { 1, 3, 3, 3, 3, 4, 5 };
        int actual = NumberOfKHelper.GetNumberOfK(data, 0);
        Assert.AreEqual(actual, 0);
    }

    // 查找的数字比最后一个数字还大，不存在
    [TestMethod]
    public void GetNumberTest6()
    {
        int[] data = { 1, 3, 3, 3, 3, 4, 5 };
        int actual = NumberOfKHelper.GetNumberOfK(data, 6);
        Assert.AreEqual(actual, 0);
    }

    // 数组中的数字从头到尾都是查找的数字
    [TestMethod]
    public void GetNumberTest7()
    {
        int[] data = { 3, 3, 3, 3 };
        int actual = NumberOfKHelper.GetNumberOfK(data, 3);
        Assert.AreEqual(actual, 4);
    }

    // 数组中的数字从头到尾只有一个重复的数字，不是查找的数字
    [TestMethod]
    public void GetNumberTest8()
    {
        int[] data = { 3, 3, 3, 3 };
        int actual = NumberOfKHelper.GetNumberOfK(data, 4);
        Assert.AreEqual(actual, 0);
    }

    // 数组中只有一个数字，是查找的数字
    [TestMethod]
    public void GetNumberTest9()
    {
        int[] data = { 3 };
        int actual = NumberOfKHelper.GetNumberOfK(data, 3);
        Assert.AreEqual(actual, 1);
    }

    // 数组中只有一个数字，不是查找的数字
    [TestMethod]
    public void GetNumberTest10()
    {
        int[] data = { 3 };
        int actual = NumberOfKHelper.GetNumberOfK(data, 2);
        Assert.AreEqual(actual, 0);
    }

    // 鲁棒性测试，数组空指针
    [TestMethod]
    public void GetNumberTest11()
    {
        int actual = NumberOfKHelper.GetNumberOfK(null, 0);
        Assert.AreEqual(actual, 0);
    }

3.2 测试结果

　　（1）测试通过情况

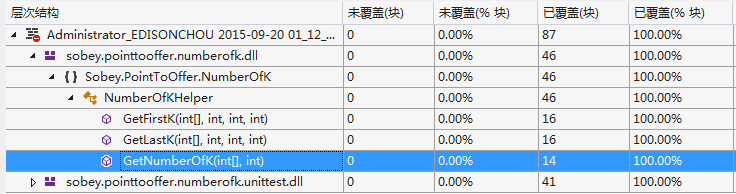
　　（2）代码覆盖率

 

作者：周旭龙

出处：http://edisonchou.cnblogs.com

本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文链接。