TreeMap源码
TreeMap是基于红黑树结构实现的一种Map,要分析TreeMap的实现首先就要对红黑树有所了解。
要了解什么是红黑树,就要了解它的存在主要是为了解决什么问题,对比其他数据结构比如数组,链表,Hash表等树这种结构又有什么优点。
1.二叉查询树、红黑树介绍
以下为个人理解,有误请拍砖。。。
下面我尽可能用通俗易懂的语言,简单总结一下数组,链表,Hash表以及树的优缺点。
1.数组,优点:(1)随机访问效率高(根据下标查询),(2)搜索效率较高(可使用折半方法)。缺点:(1)内存连续且固定,存储效率低。(2)插入和删除效率低(可能会进行数组拷贝或扩容)。
2.链表,优点:(1)不要求连续内存,内存利用率高,(2)插入和删除效率高(只需要改变指针指向)。缺点:(1)不支持随机访问,(2)搜索效率低(需要遍历)。
3.Hash表:优点:(1)搜索效率高,(2)插入和删除效率较高,缺点:(1)内存利用率低(基于数组),(2)存在散列冲突。
上面说的话比较啰嗦,再精炼一下:数组查询好、插入和删除差且浪费内存;链表插入和删除好、查询差;Hash表查询好、插入和删除也不错但是浪费内存。
也就是说,查询好的插入和删除就差,插入和删除好的查询就差,好不容易有一个查询、插入和删除都不错的,但是却又浪费内存。哎,好苦恼啊,怎么办呢,愁死我啦。能不能做到查询、插入、删除效率都很高,又不浪费内存呢。答案当然是不能!哎,还是好愁人,烦死啦。但是可以做到查询、插入、删除效率比较高,又不浪费内存。哇塞,这是什么东东,这么牛掰,这就是二叉查询树(又叫二叉排序树,又叫二叉搜索树)。你说二叉树这么好,那有什么缺点吗,有!就是算法复杂。
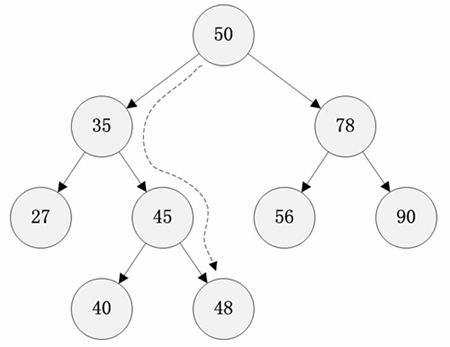
那么什么是二叉查找树呢,它又有哪些特点呢?(以下见于百度百科)
(1)若左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2)若右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3)左、右子树也分别为二叉查找树;
(4)没有键值相等的节点。
按照二叉查找树存储的数据,对元素的搜索效率是非常高的,比如上图中如果要查找值为48的节点,只需要遍历4个节点就能完成。理论上,一颗平衡的二叉查找树的任意节点平均查找效率为树的高度h,即O(lgn)。但是如果二叉查找树的失去平衡(元素全在一侧),搜索效率就退化为O(n),因此二叉查找树的平衡是搜索效率的关键所在。而
红黑树就是靠红黑规则来维持二叉查找树的平衡性。
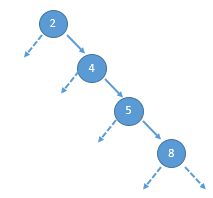
(一颗失去平衡的二叉树)
简单用代码描述上面的二叉查找树,试试看:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
|
public
class
BinaryTree {
// 二叉树的根节点
public
TreeNode rootNode ;
// 记录搜索深度
public
int
count;
/**
* 利用传入一个数组来建立二叉树
*/
public
BinaryTree(
int
[] data) {
for
(
int
i =
0
; i < data. length; i++) {
addNodeToTree(data[i]);
}
}
/**
* 将指定的值加入到二叉树中适当的节点
*/
private
void
addNodeToTree(
int
value) {
TreeNode currentNode = rootNode;
// 建立树根
if
(rootNode ==
null
) {
rootNode =
new
TreeNode(value);
return
;
}
// 建立二叉树
while
(
true
) {
// 新增的value比节点的value小,则在左子树
if
(value < currentNode.value ) {
if
(currentNode.leftNode ==
null
) {
currentNode. leftNode =
new
TreeNode(value);
return
;
}
else
{
currentNode = currentNode. leftNode;
}
}
else
{
// 新增的value比节点的value大,在右子树
if
(currentNode.rightNode ==
null
) {
currentNode. rightNode =
new
TreeNode(value);
return
;
}
else
{
currentNode = currentNode. rightNode;
}
}
}
}
/**
* 中序遍历(左子树 -树根- 右子树)
*/
public
void
inOrder(TreeNode node) {
if
(node !=
null
) {
inOrder(node. leftNode);
System. out.print(
"["
+ node.value +
"]"
);
inOrder(node. rightNode);
}
}
/**
* 前序遍历(树根 -左子树- 右子树)
*/
public
void
preOrder(TreeNode node) {
if
(node !=
null
) {
System. out.print(
"["
+ node.value +
"]"
);
preOrder(node. leftNode);
preOrder(node. rightNode);
}
}
/**
* 后序遍历(左子树 -右子树- 树根)
*/
public
void
postOrder(TreeNode node) {
if
(node !=
null
) {
postOrder(node. leftNode);
postOrder(node. rightNode);
System. out.print(
"["
+ node.value +
"]"
);
}
}
/**
* 从二叉树中查找指定value
*/
public
boolean
findTree(TreeNode node,
int
value) {
if
(node ==
null
) {
System. out.println(
"共搜索"
+ count +
"次"
);
return
false
;
}
else
if
(node.value == value) {
System. out.println(
"共搜索"
+ count +
"次"
);
return
true
;
}
else
if
(value < node.value) {
count++;
return
findTree(node.leftNode , value);
}
else
{
count++;
return
findTree(node.rightNode , value);
}
}
/**
* 利用中序遍历进行排序
*/
public
void
sort() {
this
.inOrder(rootNode );
}
class
TreeNode {
int
value ;
TreeNode leftNode;
TreeNode rightNode;
public
TreeNode(
int
value) {
this
.value = value;
this
.leftNode =
null
;
this
.rightNode =
null
;
}
}
public
static
void
main(String[] args) {
int
[] content = {
50
,
35
,
27
,
45
,
40
,
48
,
78
,
56
,
90
};
BinaryTree tree =
new
BinaryTree(content);
System. out.println(
"前序遍历:"
);
tree.preOrder(tree. rootNode);
System. out.println(
"\n中序遍历:"
);
tree.inOrder(tree. rootNode);
System. out.println(
"\n后序遍历:"
);
tree.postOrder(tree. rootNode);
System. out.println(
"\n\n开始搜索:"
);
boolean
isFind = tree.findTree(tree.rootNode,
48
);
System. out.println(
"是否搜索到"
+
48
+
":"
+ isFind);
System. out.println(
"\n进行排序:"
);
tree.sort();
}
}
|
看下运行结果:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
|
前序遍历:
[
50
][
35
][
27
][
45
][
40
][
48
][
78
][
56
][
90
]
中序遍历:
[
27
][
35
][
40
][
45
][
48
][
50
][
56
][
78
][
90
]
后序遍历:
[
27
][
40
][
48
][
45
][
35
][
56
][
90
][
78
][
50
]
开始搜索:
共搜索
3
次
是否搜索到
48
:
true
进行排序:
[
27
][
35
][
40
][
45
][
48
][
50
][
56
][
78
][
90
]
|
通过上面代码是不是对二叉查询树有所认识呢,那么,红黑树的红黑规则到底是什么呢?
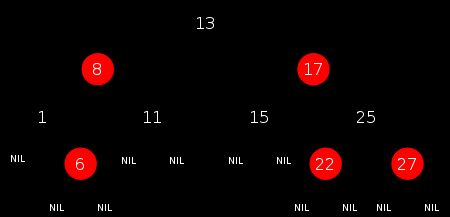
(1)节点是红色或黑色。
(2)根节点是黑色。
(3)每个叶节点(NIL节点,空节点)是黑色的。
(4)每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
(5)从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
上面的规则前4条都好理解,第5条规则到底是什么情况,下面简单解释下,比如图中红8到1左边的叶子节点的路径包含两个黑色节点,到6下面的叶子节点的路径也包含两个黑色节点。
但是在在添加或删除节点后,红黑树就发生了变化,可能不再满足上面的5个特性,为了保持红黑树的以上特性,就有了三个动作:左旋、右旋、着色。
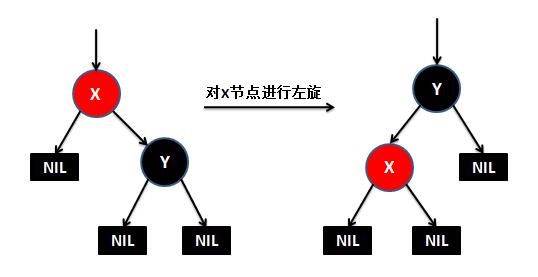
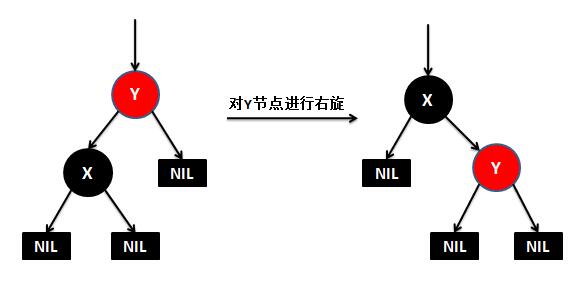
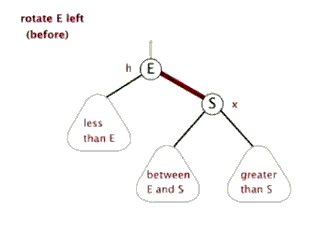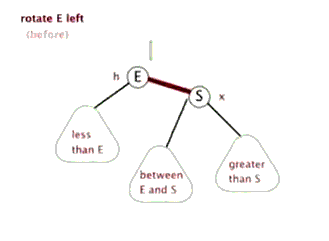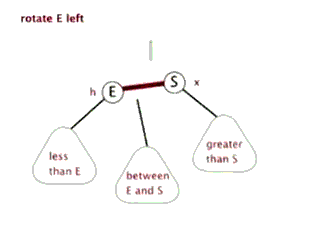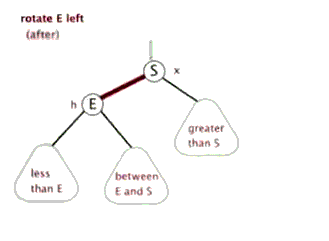
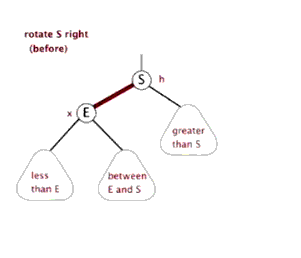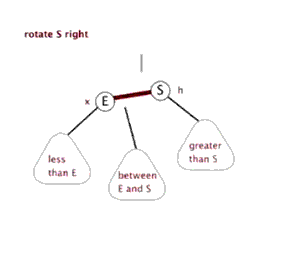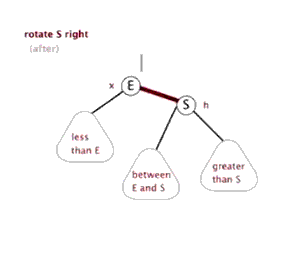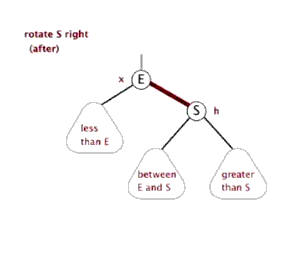
下面来看下什么是红黑树的左旋和右旋:
对x进行左旋,意味着”将x变成一个左节点”。
对y进行右旋,意味着”将y变成一个右节点”。
如果还是没看明白,下面找了两张左旋和右旋的动态图( http://www.cnblogs.com/yangecnu/p/Introduce-Red-Black-Tree.html):
ok,对二叉树、红黑树的概念有所了解后,我们来看下红黑树的两个主要逻辑添加和删除,看看TreeMap是怎么实现的。
2.TreeMap的底层实现
首先来看下TreeMap的定义:
|
1
2
3
|
public
class
TreeMap<K,V>
extends
AbstractMap<K,V>
implements
NavigableMap<K,V>, Cloneable, java.io.Serializable
|
可以看到TreeMap继承了AbstractMap抽象类,并实现NavigableMap、Cloneable、Serializable接口。NavigableMap接口扩展了SortedMap,主要是提供了给定搜索目标返回最接近匹配项的导航方法。这个不是我们今天的重点,这里不做分析了。
下面再看下TreeMap的底层存储相关定义:
|
1
2
3
4
5
6
7
8
9
10
11
|
// 比较器
private
final
Comparator<?
super
K> comparator;
// 红黑树根节点
private
transient
Entry<K,V> root =
null
;
// 集合元素数量
private
transient
int
size =
0
;
// "fail-fast"集合修改记录
private
transient
int
modCount =
0
;
|
这里的Comparator是一个比较器,这里不详细讲解,后面会单独进行分析,这里只要明白,一个类实现了Comparator接口并重写其compare方法,就能进行比较大小。Entry是树的节点类,我们来看一下Entry的定义:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
static
final
class
Entry<K,V>
implements
Map.Entry<K,V> {
K key;
V value;
// 左孩子节点
Entry<K,V> left =
null
;
// 右孩子节点
Entry<K,V> right =
null
;
// 父节点
Entry<K,V> parent;
// 红黑树用来表示节点颜色的属性,默认为黑色
boolean
color = BLACK;
/**
* 用key,value和父节点构造一个Entry,默认为黑色
*/
Entry(K key, V value, Entry<K,V> parent) {
this
.key = key;
this
.value = value;
this
.parent = parent;
}
public
K getKey() {
return
key ;
}
public
V getValue() {
return
value ;
}
public
V setValue(V value) {
V oldValue =
this
.value ;
this
.value = value;
return
oldValue;
}
public
boolean
equals(Object o) {
if
(!(o
instanceof
Map.Entry))
return
false
;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return
valEquals( key,e.getKey()) && valEquals( value,e.getValue());
}
public
int
hashCode() {
int
keyHash = (key ==
null
?
0
: key.hashCode());
int
valueHash = (value ==
null
?
0
: value.hashCode());
return
keyHash ^ valueHash;
}
public
String toString() {
return
key +
"="
+ value;
}
}
|
Entry类理解起来比较简单(因为我们前面看过很多的Entry类了),主要是定义了树的孩子和父亲节点引用,和红黑颜色属性,并对equals和hashCode进行重写,以利于比较是否相等。
3.TreeMap的构造方法
接下来看下TreeMap的构造方法:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
/**
* 默认构造方法,comparator为空,代表使用key的自然顺序来维持TreeMap的顺序,这里要求key必须实现Comparable接口
*/
public
TreeMap() {
comparator =
null
;
}
/**
* 用指定的比较器构造一个TreeMap
*/
public
TreeMap(Comparator<?
super
K> comparator) {
this
.comparator = comparator;
}
/**
* 构造一个指定map的TreeMap,同样比较器comparator为空,使用key的自然顺序排序
*/
public
TreeMap(Map<?
extends
K, ?
extends
V> m) {
comparator =
null
;
putAll(m);
}
/**
* 构造一个指定SortedMap的TreeMap,根据SortedMap的比较器来来维持TreeMap的顺序
*/
public
TreeMap(SortedMap<K, ?
extends
V> m) {
comparator = m.comparator();
try
{
buildFromSorted(m.size(), m.entrySet().iterator(),
null
,
null
);
}
catch
(java.io.IOException cannotHappen) {
}
catch
(ClassNotFoundException cannotHappen) {
}
}
|
从构造方法中可以看出,要创建一个红黑树实现的TreeMap必须要有一个用于比较大小的比较器,因为只有能够比较大小才能实现红黑树的左孩子<树根<右孩子的特点。
4.红黑树的添加原理及TreeMap的put实现
将一个节点添加到红黑树中,通常需要下面几个步骤:
(1)将红黑树当成一颗二叉查找树,将节点插入。
这一步比较简单,就上开始我们自己写的二叉查找树的操作一样,至于为什么可以这样插入,是因为红黑树本身就是一个二叉查找树。
(2)将新插入的节点设置为红色
有没有疑问,为什么新插入的节点一定要是红色的,因为新插入节点为红色,不会违背红黑规则第(5)条,少违背一条就少处理一种情况。
(3)通过旋转和着色,使它恢复平衡,重新变成一颗符合规则的红黑树。
要想知道怎么样进行左旋和右旋,首先就要知道为什么要进行左旋和右旋。
我们来对比下红黑树的规则和新插入节点后的情况,看下新插入节点会违背哪些规则。
(1)节点是红色或黑色。
这一点肯定是不会违背的了。
(2)根节点是黑色。
这一点也不会违背了,如果是根节点,只需将根节点插入就好了,因为默认是黑色。
(3)每个叶节点(NIL节点,空节点)是黑色的。
这一点也不会违背的,我们插入的是非空的节点,不会影响空节点。
(4)每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
这一点是有可能违背的,我们将新插入的节点都设置成红色,如果其父节点也是红色的话,那就产生冲突了。
(5)从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
这一点也不会违背,因为我们将新插入的节点都设置成红色。
了解了红黑树左旋和右旋操作,以及新插入节点主要是可能会违背红黑树的规则(4)后,我们来分析下,添加新节点的过程有哪几种情况:
(1)新插入节点为跟节点。这种情况直接将新插入节点设置为跟节点即可,无需进行后续的旋转和着色处理。
(2)新插入节点的父节点是黑色。这种情况直接将新节点插入即可,不会违背规则(4).
(3)新插入节点的父节点是红色。这种情况会违背规则(4),而这种情况又分为了以下几种,下面进行图解:
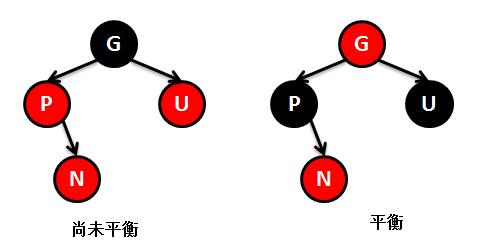
①新插入节点N的父节点P和叔叔节点U都是红色。方法是:
将祖父节点G设置为红色,父节点P和叔叔节点U设置为黑色,这时候就看似平衡了。
但是,如果祖父节点G的父节点也是红色,这时候又违背规则(4)了,怎么办,方法是:将GPUN这一组看成一个新的节点,按照前面的方案递归;
又但是根节点为红就违反规则(2)了,怎么办,方法是直接将根节点设置为黑色(两个连续黑色是没问题的)。
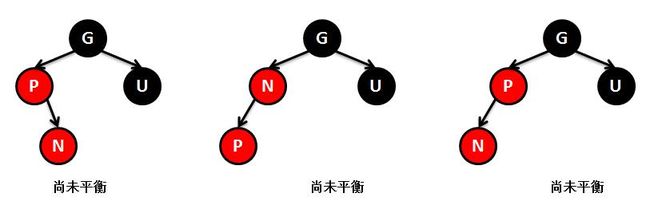
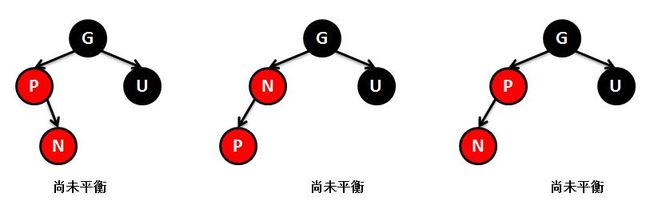
②新插入节点N的父节点P是红色,叔叔节点U是黑色或者缺少,且新节点N是P的右孩子。方法是:
左旋父节点P。左旋后N和P角色互换,但是P和N还是连续的两个红色节点,还没有平衡,怎么办,看第三种情况。
③新插入节点N的父节点P是红色,叔叔节点U是黑色或者缺少,且新节点N是P的左孩子。方法是:
右旋祖父节点G,然后将P设置为黑色,G设置为红色,达到平衡。此时父节点P是黑色,所有不用担心P的父节点是红色。
当然上面说的三种情况都是基于一个前提:新插入节点N的父节点P是祖父节点G的左孩子,如果P是G的右孩子又是什么情况呢?其实情况和上面是相似的,只需要调整左旋还是右旋,这里就不细讲了。
上面分析了这么多,到底TreeMap是怎么实现的呢,我们来看下:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
|
public
V put(K key, V value) {
// 根节点
Entry<K,V> t = root;
// 如果根节点为空,则直接创建一个根节点,返回
if
(t ==
null
) {
// TBD:
// 5045147: (coll) Adding null to an empty TreeSet should
// throw NullPointerException
//
// compare(key, key); // type check
root =
new
Entry<K,V>(key, value,
null
);
size =
1
;
modCount++;
return
null
;
}
// 记录比较结果
int
cmp;
Entry<K,V> parent;
// split comparator and comparable paths
// 当前使用的比较器
Comparator<?
super
K> cpr = comparator ;
// 如果比较器不为空,就是用指定的比较器来维护TreeMap的元素顺序
if
(cpr !=
null
) {
// do while循环,查找key要插入的位置(也就是新节点的父节点是谁)
do
{
// 记录上次循环的节点t
parent = t;
// 比较当前节点的key和新插入的key的大小
cmp = cpr.compare(key, t. key);
// 新插入的key小的话,则以当前节点的左孩子节点为新的比较节点
if
(cmp <
0
)
t = t. left;
// 新插入的key大的话,则以当前节点的右孩子节点为新的比较节点
else
if
(cmp >
0
)
t = t. right;
else
// 如果当前节点的key和新插入的key想的的话,则覆盖map的value,返回
return
t.setValue(value);
// 只有当t为null,也就是没有要比较节点的时候,代表已经找到新节点要插入的位置
}
while
(t !=
null
);
}
else
{
// 如果比较器为空,则使用key作为比较器进行比较
// 这里要求key不能为空,并且必须实现Comparable接口
if
(key ==
null
)
throw
new
NullPointerException();
Comparable<?
super
K> k = (Comparable<?
super
K>) key;
// 和上面一样,喜欢查找新节点要插入的位置
do
{
parent = t;
cmp = k.compareTo(t. key);
if
(cmp <
0
)
t = t. left;
else
if
(cmp >
0
)
t = t. right;
else
return
t.setValue(value);
}
while
(t !=
null
);
}
// 找到新节点的父节点后,创建节点对象
Entry<K,V> e =
new
Entry<K,V>(key, value, parent);
// 如果新节点key的值小于父节点key的值,则插在父节点的左侧
if
(cmp <
0
)
parent. left = e;
// 如果新节点key的值大于父节点key的值,则插在父节点的右侧
else
parent. right = e;
// 插入新的节点后,为了保持红黑树平衡,对红黑树进行调整
fixAfterInsertion(e);
// map元素个数+1
size++;
modCount++;
return
null
;
}
/** 新增节点后对红黑树的调整方法 */
private
void
fixAfterInsertion(Entry<K,V> x) {
// 将新插入节点的颜色设置为红色
x. color = RED;
// while循环,保证新插入节点x不是根节点或者新插入节点x的父节点不是红色(这两种情况不需要调整)
while
(x !=
null
&& x != root && x. parent.color == RED) {
// 如果新插入节点x的父节点是祖父节点的左孩子
if
(parentOf(x) == leftOf(parentOf (parentOf(x)))) {
// 取得新插入节点x的叔叔节点
Entry<K,V> y = rightOf(parentOf (parentOf(x)));
// 如果新插入x的父节点是红色-------------------①
if
(colorOf(y) == RED) {
// 将x的父节点设置为黑色
setColor(parentOf (x), BLACK);
// 将x的叔叔节点设置为黑色
setColor(y, BLACK);
// 将x的祖父节点设置为红色
setColor(parentOf (parentOf(x)), RED);
// 将x指向祖父节点,如果x的祖父节点的父节点是红色,按照上面的步奏继续循环
x = parentOf(parentOf (x));
}
else
{
// 如果新插入x的叔叔节点是黑色或缺少,且x的父节点是祖父节点的右孩子-------------------②
if
(x == rightOf( parentOf(x))) {
// 左旋父节点
x = parentOf(x);
rotateLeft(x);
}
// 如果新插入x的叔叔节点是黑色或缺少,且x的父节点是祖父节点的左孩子-------------------③
// 将x的父节点设置为黑色
setColor(parentOf (x), BLACK);
// 将x的祖父节点设置为红色
setColor(parentOf (parentOf(x)), RED);
// 右旋x的祖父节点
rotateRight( parentOf(parentOf (x)));
}
}
else
{
// 如果新插入节点x的父节点是祖父节点的右孩子,下面的步奏和上面的相似,只不过左旋右旋的区分,不在细讲
Entry<K,V> y = leftOf(parentOf (parentOf(x)));
if
(colorOf(y) == RED) {
setColor(parentOf (x), BLACK);
setColor(y, BLACK);
setColor(parentOf (parentOf(x)), RED);
x = parentOf(parentOf (x));
}
else
{
if
(x == leftOf( parentOf(x))) {
x = parentOf(x);
rotateRight(x);
}
setColor(parentOf (x), BLACK);
setColor(parentOf (parentOf(x)), RED);
rotateLeft( parentOf(parentOf (x)));
}
}
}
// 最后将根节点设置为黑色,不管当前是不是红色,反正根节点必须是黑色
root.color = BLACK;
}
/**
* 对红黑树的节点(x)进行左旋转
*
* 左旋示意图(对节点x进行左旋):
* px px
* / /
* x y
* / \ --(左旋)-- / \
* lx y x ry
* / \ / \
* ly ry lx ly
*
*/
private
void
rotateLeft(Entry<K,V> p) {
if
(p !=
null
) {
// 取得要选择节点p的右孩子
Entry<K,V> r = p. right;
// "p"和"r的左孩子"的相互指向...
// 将"r的左孩子"设为"p的右孩子"
p. right = r.left ;
// 如果r的左孩子非空,将"p"设为"r的左孩子的父亲"
if
(r.left !=
null
)
r. left.parent = p;
// "p的父亲"和"r"的相互指向...
// 将"p的父亲"设为"y的父亲"
r. parent = p.parent ;
// 如果"p的父亲"是空节点,则将r设为根节点
if
(p.parent ==
null
)
root = r;
// 如果p是它父节点的左孩子,则将r设为"p的父节点的左孩子"
else
if
(p.parent. left == p)
p. parent.left = r;
else
// 如果p是它父节点的左孩子,则将r设为"p的父节点的左孩子"
p. parent.right = r;
// "p"和"r"的相互指向...
// 将"p"设为"r的左孩子"
r. left = p;
// 将"p的父节点"设为"r"
p. parent = r;
}
}
/**
* 对红黑树的节点进行右旋转
*
* 右旋示意图(对节点y进行右旋):
* py py
* / /
* y x
* / \ --(右旋)-- / \
* x ry lx y
* / \ / \
* lx rx rx ry
*
*/
private
void
rotateRight(Entry<K,V> p) {
if
(p !=
null
) {
// 取得要选择节点p的左孩子
Entry<K,V> l = p. left;
// 将"l的右孩子"设为"p的左孩子"
p. left = l.right ;
// 如果"l的右孩子"不为空的话,将"p"设为"l的右孩子的父亲"
if
(l.right !=
null
) l. right.parent = p;
// 将"p的父亲"设为"l的父亲"
l. parent = p.parent ;
// 如果"p的父亲"是空节点,则将l设为根节点
if
(p.parent ==
null
)
root = l;
// 如果p是它父节点的右孩子,则将l设为"p的父节点的右孩子"
else
if
(p.parent. right == p)
p. parent.right = l;
//如果p是它父节点的左孩子,将l设为"p的父节点的左孩子"
else
p.parent .left = l;
// 将"p"设为"l的右孩子"
l. right = p;
// 将"l"设为"p父节点"
p. parent = l;
}
}
|
单纯的看代码和注释,绝对会发出,cha这是什么乱七八糟的,任谁也看不懂,所以一定要结合上面的图解,不懂了就看看图,然后动手画一下。如果你告诉我,还是没有懂,没问题可以理解,这里有一位大神录制的红黑树增加元素视频动画,来吧, http://v.youku.com/v_show/id_XNjI4NzgxMjA4.html(视频不是我录得,尊重版权,向大神致敬)。
5.红黑树的删除原理及TreeMap的remove实现
相比添加,红黑树的删除显得更加复杂了。看下红黑树的删除需要哪几个步奏:
(1)将红黑树当成一颗二叉查找树,将节点删除。
(2)通过旋转和着色,使它恢复平衡,重新变成一颗符合规则的红黑树。
删除节点的关键是:
(1)如果删除的是红色节点,不会违背红黑树的规则。
(2)
如果删除的是黑色节点,那么这个路径上就少了一个黑色节点,则违背了红黑树的规则。
来看下红黑树删除节点会有哪几种情况:
(1)被删除的节点没有孩子节点,即叶子节点。可直接删除。
(2)被删除的节点只有一个孩子节点,那么直接删除该节点,然后用它的孩子节点顶替它的位置。
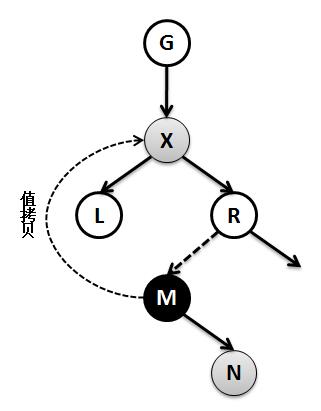
(3)被删除的节点有两个孩子节点。这种情况二叉树的删除有一个技巧,就是查找到要删除的节点X,接着我们找到它左子树的最大元素M,或者它右子树的最小元素M,交换X和M的值,然后删除节点M。此时M就最多只有一个子节点N(若是左子树则没有右子节点,若是右子树则没有左子节点 ),若M没有孩子则进入(1)的情况,否则进入(2)的情况。
如上图,我们假定节点X是要删除的节点,而节点M是找到X右子树的最小元素,所以节点M是X的替代节点,也就是说M是真正要删除的节点。上面我们分析了此时的M只会有一个子节点N,当删除节点M后,N将替代M作为M节点的父节点的子节点。删除的节点M是黑色(删除红色不影响上面分析了),此时如果N是红色,只需将N设置为黑色,就会重新达到平衡,不会出现该路径上少了一个黑色节点的情况;但是如果N是红色,情况则比较复杂,需要对红黑树进行调整,而这种情况又分为了以下几种,下面进行图解:
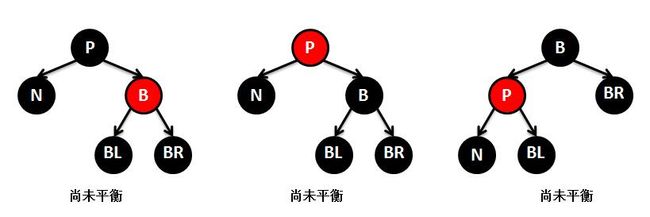
①N的兄弟节点B是红色。方法是:
交换P和B的颜色,左旋父节点P。此时并未完成平衡,左子树仍然少了一个黑色节点,进入情况③。(B为红色,P必然为黑色)
②N的父节点P是黑色,且兄弟节点B和它的两个孩子节点也都是黑色。方法是:
将N的兄弟节点B改为红色,这样从P出发到叶子节点的路径都包含了相同的黑色节点,
但是,对于节点P这个子树,P的父节点G到P的叶子节点路径上的黑色节点就少了一个,
此时需要将P整体看做一个节点,继续调整。
③N的父节点P为红色,兄弟节点B和它的两个孩子节点也都是黑色。
此时只需要交换P和B的颜色,将P改为黑色,B改为红色,则可到达平衡。这相当于既然节点N路径少了一个黑色节点,那么B路径也少一个黑色节点,这两个路径达到平衡,为了防止P路径少一个黑色节点,将P节点置黑,则达到最终平衡。
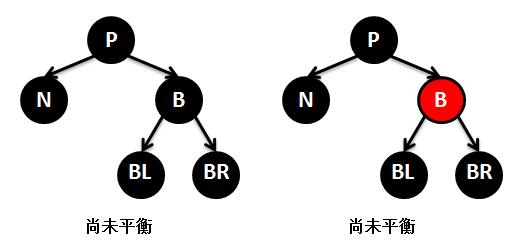
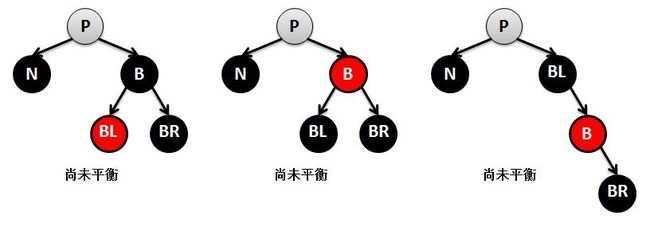
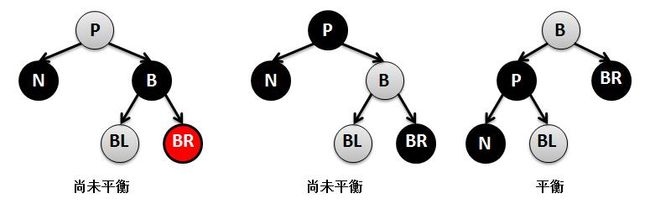
④N的兄弟节点B是黑色,B的左孩子节点BL是红色,B的右孩子节点BR是黑色,P为任意颜色。方法是:交换B和BL的颜色,右旋节点B。此时N子树路径并没有增加黑色节点,也就是没有达到平衡,此时进入下一种情况⑤。
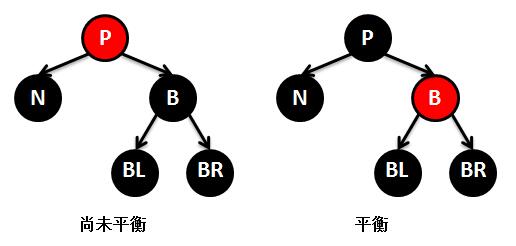
⑤N的兄弟节点B是黑色,B的右孩子节点BR是红色,B的左孩子节点BL任意颜色,P任意颜色。方法是:BR变为黑色,P变为黑色,B变为P的颜色;左旋节点B。首先给N路径增加一个黑色节点P,P原位置上的颜色不变;S路径少了一个黑色节点,于是将BR改为黑色,最终达到了平衡。
上面对红黑树删除的原理和删除过程中遇到的情况进行了分析说明,我们得到的结论是红黑树的删除遇到的主要问题就是被删除路径上的黑色节点减少,于是需要进行一系列旋转和着色,
当然上面的情况是基于M是X右子树的最小元素,而M如果是X左子树的最大元素和上面的情况是相似的,我们具体看下TreeMap的代码是怎么实现的:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
|
public
V remove(Object key) {
// 根据key查找到对应的节点对象
Entry<K,V> p = getEntry(key);
if
(p ==
null
)
return
null
;
// 记录key对应的value,供返回使用
V oldValue = p. value;
// 删除节点
deleteEntry(p);
return
oldValue;
}
private
void
deleteEntry(Entry<K,V> p) {
modCount++;
// map容器的元素个数减一
size--;
// If strictly internal, copy successor's element to p and then make p
// point to successor.
// 如果被删除的节点p的左孩子和右孩子都不为空,则查找其替代节点-----------这里表示要删除的节点有两个孩子(3)
if
(p.left !=
null
&& p. right !=
null
) {
// 查找p的替代节点
Entry<K,V> s = successor (p);
p. key = s.key ;
p. value = s.value ;
// 将p指向替代节点,※※※※※※从此之后的p不再是原先要删除的节点p,而是替代者p(就是图解里面讲到的M) ※※※※※※
p = s;
}
// p has 2 children
// Start fixup at replacement node, if it exists.
// replacement为替代节点p的继承者(就是图解里面讲到的N),p的左孩子存在则用p的左孩子替代,否则用p的右孩子
Entry<K,V> replacement = (p. left !=
null
? p.left : p. right);
if
(replacement !=
null
) {
// 如果上面的if有两个孩子不通过--------------这里表示要删除的节点只有一个孩子(2)
// Link replacement to parent
// 将p的父节点拷贝给替代节点
replacement. parent = p.parent ;
// 如果替代节点p的父节点为空,也就是p为跟节点,则将replacement设置为根节点
if
(p.parent ==
null
)
root = replacement;
// 如果替代节点p是其父节点的左孩子,则将replacement设置为其父节点的左孩子
else
if
(p == p.parent. left)
p. parent.left = replacement;
// 如果替代节点p是其父节点的左孩子,则将replacement设置为其父节点的右孩子
else
p. parent.right = replacement;
// Null out links so they are OK to use by fixAfterDeletion.
// 将替代节点p的left、right、parent的指针都指向空,即解除前后引用关系(相当于将p从树种摘除),使得gc可以回收
p. left = p.right = p.parent =
null
;
// Fix replacement
// 如果替代节点p的颜色是黑色,则需要调整红黑树以保持其平衡
if
(p.color == BLACK)
fixAfterDeletion(replacement);
}
else
if
(p.parent ==
null
) {
// return if we are the only node.
// 如果要替代节点p没有父节点,代表p为根节点,直接删除即可
root =
null
;
}
else
{
// No children. Use self as phantom replacement and unlink.
// 判断进入这里说明替代节点p没有孩子--------------这里表示没有孩子则直接删除(1)
// 如果p的颜色是黑色,则调整红黑树
if
(p.color == BLACK)
fixAfterDeletion(p);
// 下面删除替代节点p
if
(p.parent !=
null
) {
// 解除p的父节点对p的引用
if
(p == p.parent .left)
p. parent.left =
null
;
else
if
(p == p.parent. right)
p. parent.right =
null
;
// 解除p对p父节点的引用
p. parent =
null
;
}
}
}
/**
* 查找要删除节点的替代节点
*/
static
<K,V> TreeMap.Entry<K,V> successor(Entry<K,V> t) {
if
(t ==
null
)
return
null
;
// 查找右子树的最左孩子
else
if
(t.right !=
null
) {
Entry<K,V> p = t. right;
while
(p.left !=
null
)
p = p. left;
return
p;
}
else
{
// 查找左子树的最右孩子
Entry<K,V> p = t. parent;
Entry<K,V> ch = t;
while
(p !=
null
&& ch == p. right) {
ch = p;
p = p. parent;
}
return
p;
}
}
/** From CLR */
private
void
fixAfterDeletion(Entry<K,V> x) {
// while循环,保证要删除节点x不是跟节点,并且是黑色(根节点和红色不需要调整)
while
(x != root && colorOf (x) == BLACK) {
// 如果要删除节点x是其父亲的左孩子
if
(x == leftOf( parentOf(x))) {
// 取出要删除节点x的兄弟节点
Entry<K,V> sib = rightOf(parentOf (x));
// 如果删除节点x的兄弟节点是红色---------------------------①
if
(colorOf(sib) == RED) {
// 将x的兄弟节点颜色设置为黑色
setColor(sib, BLACK);
// 将x的父节点颜色设置为红色
setColor(parentOf (x), RED);
// 左旋x的父节点
rotateLeft( parentOf(x));
// 将sib重新指向旋转后x的兄弟节点 ,进入else的步奏③
sib = rightOf(parentOf (x));
}
// 如果x的兄弟节点的两个孩子都是黑色-------------------------③
if
(colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf (sib)) == BLACK) {
// 将兄弟节点的颜色设置为红色
setColor(sib, RED);
// 将x的父节点指向x,如果x的父节点是黑色,需要将x的父节点整天看做一个节点继续调整-------------------------②
x = parentOf(x);
}
else
{
// 如果x的兄弟节点右孩子是黑色,左孩子是红色-------------------------④
if
(colorOf(rightOf(sib)) == BLACK) {
// 将x的兄弟节点的左孩子设置为黑色
setColor(leftOf (sib), BLACK);
// 将x的兄弟节点设置为红色
setColor(sib, RED);
// 右旋x的兄弟节点
rotateRight(sib);
// 将sib重新指向旋转后x的兄弟节点,进入步奏⑤
sib = rightOf(parentOf (x));
}
// 如果x的兄弟节点右孩子是红色-------------------------⑤
setColor(sib, colorOf (parentOf(x)));
// 将x的父节点设置为黑色
setColor(parentOf (x), BLACK);
// 将x的兄弟节点的右孩子设置为黑色
setColor(rightOf (sib), BLACK);
// 左旋x的父节点
rotateLeft( parentOf(x));
// 达到平衡,将x指向root,退出循环
x = root;
}
}
else
{
// symmetric // 如果要删除节点x是其父亲的右孩子,和上面情况一样,这里不再细讲
Entry<K,V> sib = leftOf(parentOf (x));
if
(colorOf(sib) == RED) {
setColor(sib, BLACK);
setColor(parentOf (x), RED);
rotateRight( parentOf(x));
sib = leftOf(parentOf (x));
}
if
(colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf (sib)) == BLACK) {
setColor(sib, RED);
x = parentOf(x);
}
else
{
if
(colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf (sib), BLACK);
setColor(sib, RED);
rotateLeft(sib);
sib = leftOf(parentOf (x));
}
setColor(sib, colorOf (parentOf(x)));
setColor(parentOf (x), BLACK);
setColor(leftOf (sib), BLACK);
rotateRight( parentOf(x));
x = root;
}
}
}
setColor(x, BLACK);
}
|
删除相对来说更加复杂,还是那句话一定要对照着图解看代码,否则是读不懂的,别问我是怎么看懂得,我n天不看再看代码也不知道123了。
终于看完了红黑树的增加和删除,下面来看个稍微简单的查询:
6.红黑树的查询
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
|
public
V get(Object key) {
Entry<K,V> p = getEntry(key);
return
(p==
null
?
null
: p. value);
}
final
Entry<K,V> getEntry(Object key) {
// Offload comparator-based version for sake of performance
if
(comparator !=
null
)
// 如果比较器为空,只是用key作为比较器查询
return
getEntryUsingComparator(key);
if
(key ==
null
)
throw
new
NullPointerException();
Comparable<?
super
K> k = (Comparable<?
super
K>) key;
// 取得root节点
Entry<K,V> p = root;
// 从root节点开始查找,根据比较器判断是在左子树还是右子树
while
(p !=
null
) {
int
cmp = k.compareTo(p.key );
if
(cmp <
0
)
p = p. left;
else
if
(cmp >
0
)
p = p. right;
else
return
p;
}
return
null
;
}
final
Entry<K,V> getEntryUsingComparator(Object key) {
K k = (K) key;
Comparator<?
super
K> cpr = comparator ;
if
(cpr !=
null
) {
Entry<K,V> p = root;
while
(p !=
null
) {
int
cmp = cpr.compare(k, p.key );
if
(cmp <
0
)
p = p. left;
else
if
(cmp >
0
)
p = p. right;
else
return
p;
}
}
return
null
;
}
|
查询看起来真的是so easy。。。
6.TreeMap对NavigableMap接口的实现
TreeMap对NavigableMap接口的实现的内容,不作为这里的重点,这些内容会和TreeSet一起分析,TreeSet见。
给jdk写注释系列之jdk1.6容器(8)-TreeSet&NavigableMap&NavigableSet源码解析
到此TreeMap就分析完了,其实大部分时间都在整理红黑树,在数据结构中树是比较难懂的一个,其算法也比较复杂,对于树的理解一定要多看图画图,要明白这么做是为了解决什么问题,这么做又有什么好处,当然看一遍看不懂就要多看几遍了。什么你问我平时工作中会用到树吗?那真的要看你做的什么性质的工作,如果是web、客户端开发,调用api就可以了对吧,如果是从事底层开发,比如文件系统,存储系统,缓存等工作必须是需要的。当然就算用不到,理解了也是有益无害的。
红黑树&TreeMap 完!