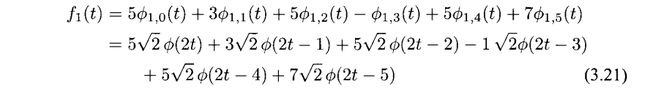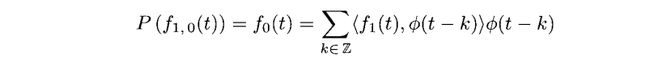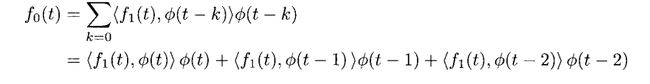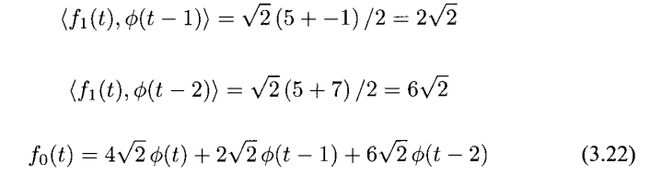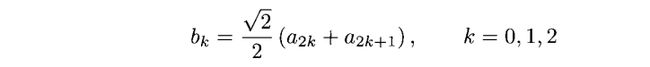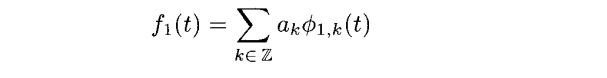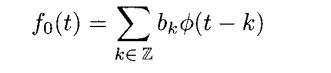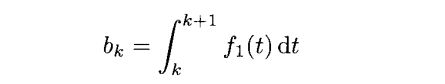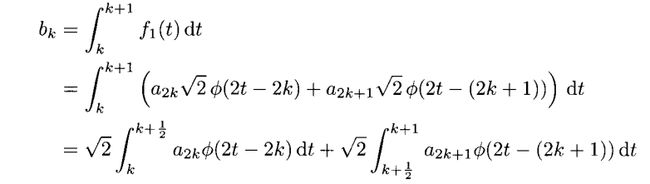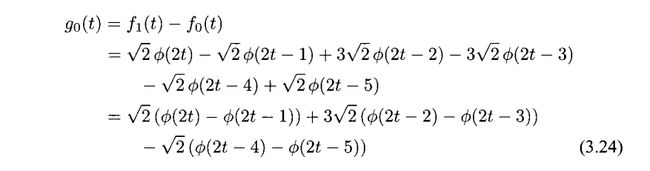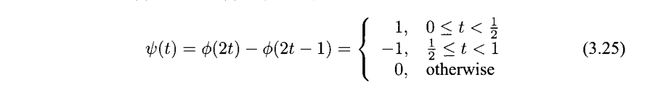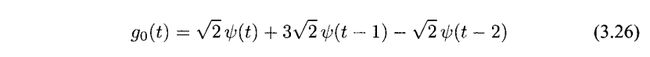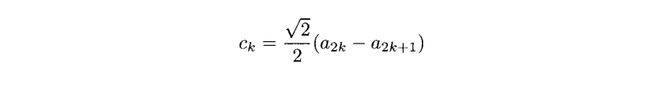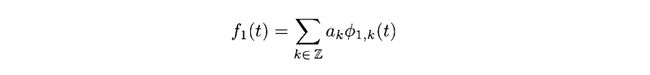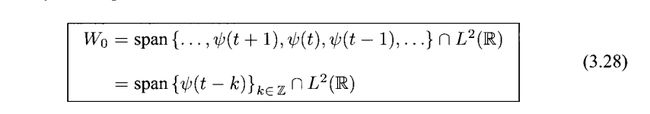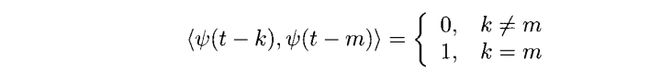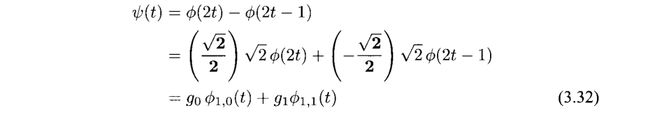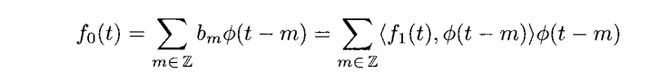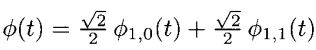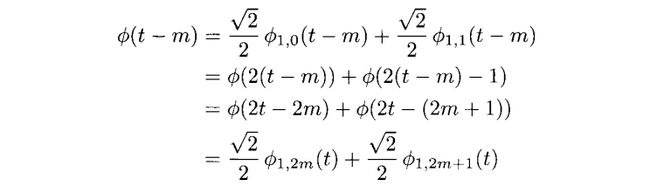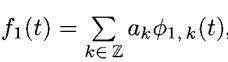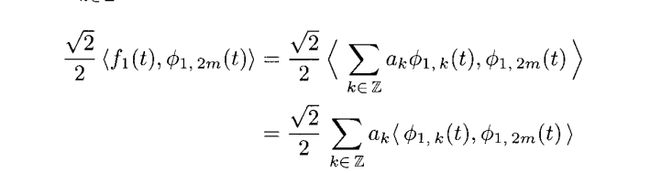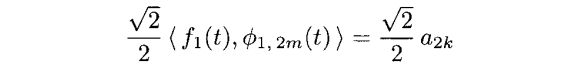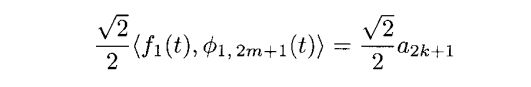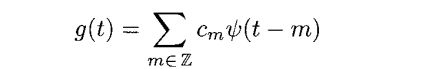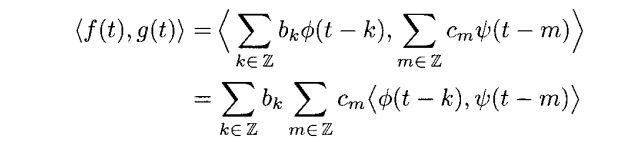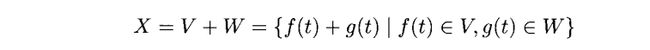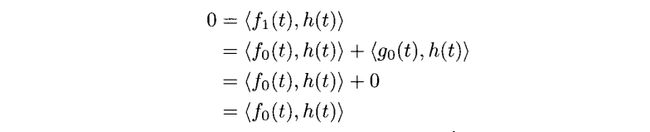3.3 哈尔小波空间W0

在3.2节我们学习了关于（3.8）定义的Vj的性质。特别的，我们可以乘以系数从一个Vj空间变换到另一个。我们这节学习V0和V1的关系。

• 将f1（t）∈V1投影至V0

我们考虑一个属于V1的函数f1（t），有

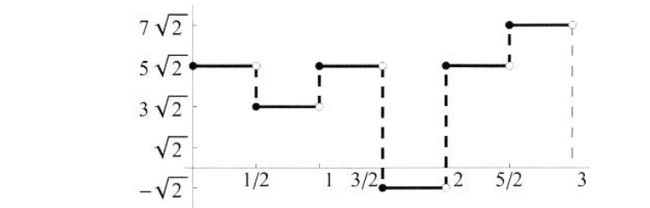
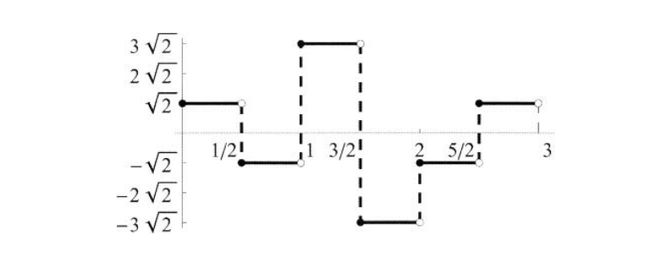
 这个函数在图3.12中画出

图3.12 函数f1（t）

从性质2.8我们知道f1（t）属于Vj，只要j≥1。然而这个函数不属于V0，因为他的间断点在。如果我们现在想找一个在V0里面的函数f0（t）来逼近f1（t），那我们可以采用在3.2小结中学习的公式来做，我们有

因为，这个函数的支撑集为，所以我们能写成以下有限和的形式

由于这个内积还是十分容易计算的，我们有

 

我们就逐一计算

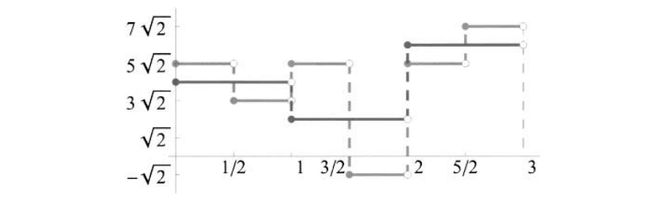
现在我们将他们都画在一张图上面

图3.13 函数f0（t）（黑）以及f1（t）（灰）

我们可以看Φ（t-k）的系数，我们不难发现，这些系数都是求平均之后再乘以根号2，我们看（3.21）的f1（t）有

其中a0=5,a1=3，a3=-1,a4=5,a5=7，然后

b0=4√2，b1=2√2,b2=5√2。我们会发现bk遵循以下规律

我们下面对这个例子进行推广，推广至所有的f1(t)∈V1

性质3.9（从V1投影到V0）如果f1（t）∈V1，表示为

同样f₁（t）的投影f₀（t）=P_f1,0（t）可以写成以下的形式

其中

（3.23）

对所有k∈Z成立

证明：让

现在我们知道，并且函数的Φ（t-k）的值为1。所以积分就变成了

由于断点在（1/2）Z 处，所以我们把函数分成两部分，其中和。其中，]

我们下面来确定m的值。

我们可以采用在3.2节的练习3.11来确定。Φ（2t-m）的支撑集为。我们将左端点m/2设定为左端，也就是说，m/2=k或者m=2k,因此Φ（2t-2k）=Φ_1,2k（t）。最左端的重叠部分为[k,k+1]。

从而我们有

因此在区间[k,k+1]

其中，支撑集，

因此内积变作

在其支撑集上Φ（2t-2k）=1，Φ（2t-（2k+1））=1.内积的结果为

证毕。

•  剩余函数g（t）=f₁（t）-f₀（t）

我们将f0(t)视作f1（t）∈V1的逼近，如果我们现在建立一个函数g(t)使得f0（t）+g0（t）=f1（t），那么f1（t）会是怎么样的呢？

我们能够非常容易的计算出g0（t）=f1（t）-f0（t），从图3.13我们可以知道g（t）是一个在1/2 ,1 ,3/2 ,2,5/2处有间断点的常分段函数。g（t）是V1的元素，能写成Φ_1,k（t）的线性组合。

我们将g0（t）写出来

 

g0（t）在图3.14中画出

图3.14 函数g0（t）

• 小波函数Ψ（t）的定义

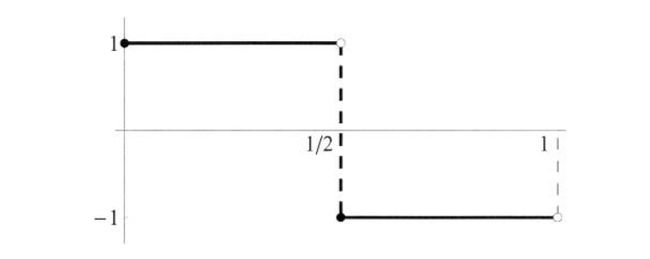
我们对g0（t）的进行更细一步的分析。如果g0（t）在[0.1)上。那么这个函数g（t）乘以√2，会形成函数Ψ（t）

图3.15 函数 Ψ（t）

我们看g0（t）在[1,2)区间内，可以看做Ψ（t）右移一个单位并乘以3√2。因此在[1.2)处，g0（t）=3√2Ψ（t-1）。同样的，我们也可以写出在区间[2,3)。g0（t）=-Ψ（t-2）。总体来说

我们应该注意到，他们的系数都是有一定的关系的。我们回忆一下（3.21）中f1（t）的系数。如果我们让

则所以，不难看出c_k遵循

•  用Ψ（t）书写g0（t）

同样的，我们对其进行推广到所有的g0（t）

性质3.10（剩余函数的公式）假设f1（t）是V1的一个函数，有

f0（t）是在v0空间对f1（t）的逼近。并且有g（t）=f1（t）-f0（t），g0（t）为

同时，Ψ（t）为（3.25），以及系数为

 

证明：证明留作练习3.22

•  空间W0的定义

回忆我们对于V0的定义，是Φ（t）以及它的整数平移的函数的线性组合。仿照这个定义，我们也规定了Ψ（t）以及它的整数平移的函数的线性组合张成以下空间

定义3.4（剩余空间W0）对于在（3.25）定义的Ψ（t），我们定义以下空间

我们称这个空间为哈尔小波函数Ψ（t）生成的哈尔小波空间。

我们看我这个小波的这个词是怎么来的，我们从f0(t)来拟合f1（t），会产生些“小”的波的误差如Ψ（t）以及它的整数平移。

通过定义张成空间W0，而且在练习3.23中你会知道，他们是线性无关的函数。同样以下的式子很容易得出（练习3.25）

从而有以下的性质

性质3.11（W0的一组正交基）对于（3.28）定义出来的空间W0，以及（3.25）定义出来的Ψ（t）来说。是它的一组正交基。

证明：这个问题留作练习3.23以及3.25

• 尺度函数以及膨胀方程

从（3.23）中你可以看见向量

在f1（t）投影到V0空间中扮演了重要的作用，因此，我们能通过（3.29）重写（3.23）。我们对于k∈Z

其中，我们能通过h来让V1里面的基函数表示Φ（t），有

 同样，我们可以使用向量

 

 将f1（t）投影进W0。正如我们在（3.25）所见的

 

 因此，我们能将Ψ（t）用V1的基函数来表示，滤波系数g0以及g1可以为其系数的线性组合。

等式（3.30）和（3.32）在小波理论中担当重要地位。函数Φ（t）生成了能让我们拟合在L2(R)里面函数的空间Vj。等式（3.30）给予我们从V0和V1空间联系的方式。

同样，Ψ（t）生成的空间W0给我们一种度量从V0拟合V1的失误程度。等式（3.32）也说明了V1里面的函数如何表示Ψ（t）。

 我们已经将Ψ（t）称作哈尔小波函数。现在我们给Φ（t）和等式（3.30）和（3.32）来命名。

定义3.5（哈尔尺度函数以及膨胀方程）我们称等式

叫膨胀方程。哈尔函数Φ（t）生成这些用于生成膨胀方程，我们称作尺度函数（作者注：Φ（t）和Ψ（t）有时候我们分别称为父小波和母小波）

• 性质3.9的另一种证法

我们将Φ（t）表示为Φ_1,0（t）和Φ_1,1（t），给予我们另一种证明性质3.9的方法

证明：让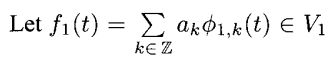，假设我们将f1（t）投影入V0，使用（3.16），我们有

而且，，因此

因此

因为我们第一个内积可以写为

因为Φ_1,k（t）和Φ_1,2m（t）是正交的，所以唯一一个非正交的内积就是k=2m 的时候，我们有

同样的，我们有

因此得到（3.23）

在练习3.27你会用（3.34）从而形成另一种方法来证明性质3.10

• 直和以及正交直和

性质3.12（V0、W0空间的正交性）如果f（t）∈V0，g(t)∈W0。则有<f(t),g(t)>=0

证明：因为f（t）∈V0，我们可以将它写作Φ（t）的线性组合

同样，

内积就是

在练习3.25（c）你会要求证明，从而完成整个的证明。

在后面的章节，我们会对正交的集合非常感兴趣，因此，我们先在这里给出定义。

定义3.6（正交空间）假设V和W是L2(R)的两个子集。如果f（t）∈V，g(t)∈W且<f(t),g(t)>=0，则称它们是正交的。写作V⊥W。

在性质3.12中，我们给出了一组符合定义3.6的例子（V0⊥W0）。

我们在性质3.10里面说到f1（t）∈V1，f1（t）=g0（t）+V0（t），其中g0∈W0，f0（t）∈V0，同时f0（t）是f1（t）在V0的投影，g0(t)是f1（t）在W0的投影。（见练习3.26）我们可以通过W0和V0里面的函数相加构造出V1里面的函数。我们给出下面这个定义

定义3.7（直和以及正交直和）假设V和W都是L2(R)的子空间，我们定义V和W的直和为

 

如果V⊥W，我们称X为正交直和，并记作

注意到，如果X=W+V，由因为0∈W，因而又有，所以有。相似的，我们也可以证明W是X的子空间。

• 从V0和W0到V1

我们已经知道了V0⊥W0，那么他们的正交直和是什么呢？下面的这个性质给出了答案

性质3.13（V0和W0的正交直和）如果V0和V1分别定义于（3.8）和（3.28），我们有

证明:从性质3.10我们知道任意f1（t）∈V1能表示为f0（t）∈V0和g0∈W0.我们也知道f0（t）和g0（t）都是V1中的元素，因此原命题等价于f1（t）∈V1与所有的h（t）∈V0正交，则f1（t）一定属于W0（译者注：下面的讨论是考虑V1在V0的投影为0的特殊情况）。假设h（t）是任意一个V0里面的函数，然后

 

 又因为h（t）是任意的，所以必须有f0（t）=0因此f1（t）∈W0，证毕。