【实数系统】 04 - 连分数

　　我们一直在不自觉地使用着十进制小数（decimal fraction）表示实数，小数运算方便、容易理解，让实数使用起来更加自如。但小数却不能提供更多关于实数本身的性质，尤其是对无理数、超越数的研究，小数表示完全无法胜任。有人会感到困惑，什么叫实数本身的性质？实数本身还有什么需要进一步研究的？比如说吧，无理数周边的有理数是如何分布的？超越数和其它无理数有什么本质区别？这些问题的回答都超出了本篇的范围，但我觉得可以从一个简单的入口来洞悉里面的世界，为今后的学习提供工具和精神上的准备。

1. 一般连分数

　　在正式给出定义之前，先来欣赏一下下面漂亮的表达式：

　　\(\sqrt{2}+1=2+\cfrac{1}{2+\cfrac{1}{2+\cdots}}\)

　　\(\dfrac{\sqrt{5}+1}{2}=1+\cfrac{1}{1+\cfrac{1}{1+\cdots}}\)

　　\(\dfrac{4}{\pi}=1+\cfrac{1^2}{2+\cfrac{2^2}{2+\cfrac{3^2}{2+\cfrac{4^2}{\cdots}}}}\)

　　\(\dfrac{e-1}{e+1}=\cfrac{1}{2+\cfrac{1}{6+\cfrac{1}{10+\cfrac{1}{14+\cdots}}}}\)

　　\(\sqrt{a^2+b}=a+\cfrac{b}{2a+\cfrac{b}{2a+\cfrac{b}{2a+\cdots}}}\)

　　这里要介绍的就是连分数（Continued Fractions），它是实数的另一种表示方法，在数论等学科中有着很惊奇的应用。简单说连分数就是具有以下左边形式的表达式，其中\(a_i,b_i\)可以是任何数（甚至复数），省略号可以是有限或无穷的。右边的表达式叫一般连分数，如果\(a_0\)为整数、\(a_k(k>0)\)为正整数，它又叫简单连分数，本篇只介绍一般连分数和简单连分数。

\[a_0+\cfrac{b_0}{a_1+\cfrac{b_1}{a_2+\cdots}};\quad\quad a_0+\cfrac{1}{a_1+\cfrac{1}{a_2+\cdots}}\]

　　这种书写方式虽然直观，但稍显繁琐，我们可以把一般连分数写成\([a_0,a_1,a_2,\cdots]\)。值得一提的是，有限连分数显然都是一个数，但无限连分数却还只是个记号，它能不能表示数还需要进一步的结论。另外，\(s_k=[a_0,a_1,\cdots,a_k]\)称为连分数的节，\(r_k=[a_k,a_{k+1},\cdots]\)称为连分数的余式，显然有下式成立：

\[[a_0,a_1,a_2,\cdots]=[a_0,a_1,\cdots,a_{k-1},r_k]\tag{1}\]

　　显然连分数的每个节\(s_k\)都可以展开为一般的分数形式\(\dfrac{p_k}{q_k}\)，它称为连分数的渐进分数（convergents），由数学归纳法可以推得如下公式。其中\(p_{-2},p_{-1},q_{-2},q_{-1}\)是补充进来的，它们可以使公式统一。这个公式非常漂亮，\(p_k,q_k\)居然独立地只与\(a_k\)相关，它是连分数理论的基本公式。

\[p_k=a_kp_{k-1}+p_{k-2};\quad (p_{-2}=0,p_{-1}=1)\tag{2}\]

\[q_k=a_kq_{k-1}+q_{k-2};\quad (q_{-2}=1,q_{-1}=0)\]

　　直觉可能已经告诉你，渐进分数可能是实数的一种逼近序列，研究渐进分数之间的关系就能知道这个逼近的趋势。将上式分别乘上\(q_{k-1},p_{k-1}\)并相减得到\(p_kq_{k-1}-q_kp_{k-1}=p_{k-2}q_{k-1}-q_{k-2}p_{k-1}\)，迭代计算得到公式（3），并进而有公式（4），用类似的方法和已有结论容易有公式（5）（6）。它们都表示了渐进分数的逼近情况，以后会经常用到。

\[q_kp_{k-1}-p_kq_{k-1}=(-1)^k\tag{3}\]

\[\dfrac{p_{k-1}}{q_{k-1}}-\dfrac{p_k}{q_k}=\dfrac{(-1)^k}{q_kq_{k-1}}\tag{4}\]

\[q_kp_{k-2}-p_kq_{k-2}=(-1)^{k-1}a_k\tag{5}\]

\[\dfrac{p_{k-2}}{q_{k-2}}-\dfrac{p_k}{q_k}=\dfrac{(-1)^{k-1}a_k}{q_kq_{k-2}}\tag{6}\]

　　你可能注意到，余式\(r_k\)完全可以当做\(a_k\)看待，所以可以有表达式（7）。这个表达式将余式和连分数的值联系了起来，对研究逼近很有用处。另外，结合公式（2）很容易得到以下有趣的表达式（8）。它们不仅漂亮，对今后的证明也都很有用。

\[[a_0,a_1,a_2,\cdots]=\dfrac{p_{k-1}r_k+p_{k-2}}{q_{k-1}r_k+q_{k-2}}\tag{7}\]

\[\dfrac{p_k}{p_{k-1}}=[a_k,a_{k-1},\cdots,a_0];\quad \quad \dfrac{q_k}{q_{k-1}}=[a_k,a_{k-1},\cdots,a_1]\tag{8}\]

2. 简单连分数

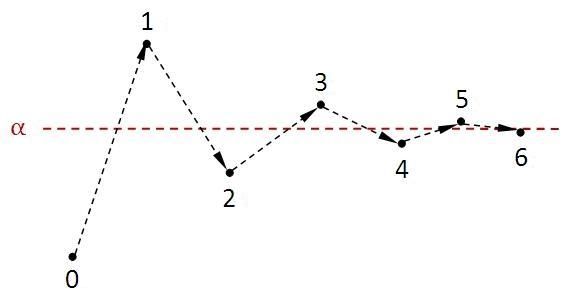
　　以上的讨论都是针对一般连分数进行的，得出的结论也都是关于表达式形式的。如果想得到关于值的性质，看来必须限制\(a_k\)的值，现在就假设\(a_k\)为正数（比简单连分数条件弱一些）。由公式（4）可知偶（奇）数项渐进分数是递增（减）的，而且奇数项皆大于偶数项。从图像上看感觉就是两条逐渐靠近的曲线，我们自然会问：它们会收敛于同一个值吗？对于有限连分数，答案是显然的，最后一项会等于分数值。但对于无限连分数，极限的知识告诉我们它们不一定相遇，所以还需要研究它们相遇的条件。

　　首先，渐进分数序列收敛时称连分数是收敛的，它本质上是说两条曲线收敛于同一值，该值称为连分数的值。容易看出连分数收敛和它的余式收敛是等价的，那么无穷连分数收敛的条件是什么呢？由公式（4）可知收敛的等价条件是\(q_kq_{k+1}\to+\infty\)，下面来证它的充要条件是\(\sum{a_k}\)发散。先证必要性，即由极限为无穷证明级数发散。首先容易有\(q_k>q_{k-2}\)，从而\(q_k>q_{k-1},q_{k-1}>q_{k-2}\)有一个成立，结合公式（2）可有\(q_k<\dfrac{1}{1-a_k}q_{k-1}\)或\(q_k<\dfrac{1}{1-a_k}q_{k-2}\)。如果级数收敛，由级数理论可知\(\prod\limits_{k=0}^\infty{(1-a_k)}\)有非零值，从而\(q_k\)有限，与极限为无穷矛盾，所以级数必收敛。再证充分性，即由级数发散可证极限为无穷。现由\(q_k\geqslant q_{k-2}+ca_k\)分别对奇偶项进行估值，合并有\(q_k+q_{k+1}>c\sum\limits_{i=0}^k{a_i}\)，然后很容易有\(q_kq_{k+1}\to+\infty\)。证明完成。

　　可以猜想，不同的连分数可能收敛到同一个实数，这样实数的连分数表示就没有唯一性。为达到唯一性，并获得更多的结论，从现在开始我们仅讨论简单连分数，并简称为连分数。连分数的\(a_k\)称为局部商（partial quotient），\(a_0\)可为负数，为保持结论的处处成立，我们再限定它必须非负，这并不影响结论对所有连分数的适用性。另外，对有限连分数有\([a_0,\cdots,a_{n-1},1]=[a_0,\cdots,a_{n-1}+1]\)，连分数表示仍然不唯一，但容易证明，如果限制\(a_n>1\)，则实数有唯一的连分数表示（十进制小数表示也要剔除掉\(\dot{9}\)才有唯一表示）。

　　比较自然地可以想到，实数的唯一连分数表示可以用类似辗转相除的方法逐步得到。每次\(a_k\)取余式\(r_k\)的整数部分，余式的小数部分取倒数得到新的余式\(r_{k+1}\)，依次类推，比如由下表可得到\(\pi=[3,7,15,1,292,1,\cdots]\)。显然有理数在有限步后余式为0，结束流程得到有限连分数，而无理数则会一直进行下去，得到无限连分数。

\(r_0=3.1415926\)	\(r_1=7.0625\)	\(r_2=15.99659\)	\(r_3=1.0034\)	\(r_4=292.634\)	\(r_5=1.575\)
\(a_0=3\)	\(a_1=7\)	\(a_2=15\)	\(a_3=1\)	\(a_4=292\)	\(a_5=1\)

　　由公式（7）可知\(\alpha=[a_0,\cdots,a_n,r_{n+1}]=\dfrac{p_kr_{k+1}+p_{k-1}}{q_kr_{k+1}+q_{k-1}}\)，其中\(a_{n+1}\leqslant r_{n+1}<a_n+1\)，从而得到渐进分数的误差估计公式（9）。该误差公式可以继续得到误差比较式（10）（11），即渐进分数越来越接近连分数的值。

\[\dfrac{1}{q_k(q_k+q_{k+1})}<\left|{\alpha-\dfrac{p_k}{q_k}}\right|\leqslant\dfrac{1}{q_kq_{k+1}}\tag{9}\]

\[\left|{\alpha-\dfrac{p_{k+1}}{q_{k+1}}}\right|<\left|{\alpha-\dfrac{p_k}{q_k}}\right|\tag{10}\]

\[\left|{q_{k+1}\alpha-p_{k+1}}\right|<\left|{q_k\alpha-p_k}\right|\tag{11}\]

 

3. 逼近的度量

　　实数的连分数表示不依赖于进制，\(a_k\)的大小一定程度上表示了逼近的程度，它是研究无理数的有力工具。连分数的渐进分数可以由公式（2）递推得到，\(p_k,q_k\)都是整数，由公式（3）得到\(p_k,q_k\)又是互质的，所以公式（2）推导出的渐进分数都是既约分数。

　　关于用有理数逼近无理数，我们有这样一个基本问题：怎样用尽量小分母的分数来逼近已知无理数？这个问题不仅有实际应用价值，还能考察一个无理数的性质。首先我们可以有这样的粗略感觉，对选定的分母可有一个最逼近的分数，随着分母的递增，必然有某个分数更加逼近，然而这些分母之间可能是有间隔的。先对这样的逼近作一个明确的定义，对任意实数\(\alpha\)，若既约分数\(\dfrac{n}{m}\)比任何分母不大于\(m\)的分数都更逼近\(\alpha\)，\(\cfrac{n}{m}\)称为\(\alpha\)的最佳逼近。即若\(m'\leqslant m\)，\(n'\)任意，则有表达式（12）。一个实数可能有很多的最佳逼近，它们分母递增，且值逐渐逼近\(\alpha\)直至收敛。

\[\left|{\alpha-\dfrac{n}{m}}\right|<\left|{\alpha-\dfrac{n'}{m'}}\right|\tag{12}\]

　　由前面的分析知道，渐进分数逐步靠近收敛值，而且它们的分母也逐渐增大，那它们是不是就是我们要找的最佳逼近呢？答案让人惊喜，但也有点让人失望，渐进分数都是最佳逼近，但不是所有最佳逼近都是渐进分数。在得到更细致的结论之前，我们需要引入中位数的概念。分数\(\dfrac{a+c}{b+d}\)称为\(\dfrac{a}{b}\)和\(\dfrac{a}{b}\)的中位数，容易证明它的值介于\(\dfrac{a}{b}\)和\(\dfrac{a}{b}\)之间（中位数定理）。

　　考察如下序列，它们和\(\dfrac{p_{k-1}}{q_{k-1}}\)之间都是中位数关系，所以这是一个单调序列，且位于收敛值的同一侧。这个序列如果再前进一步，就是\(\dfrac{p_{k-1}}{q_{k-1}}\)和\(\dfrac{p_k}{q_k}\)的中位数，同样推理，它必和\(\dfrac{p_{k-1}}{q_{k-1}}\)在同一侧。这个有趣的过程可以启发我们如何计算\(a_k\)，已知前两个渐进分数和收敛值\(\alpha\)时，可以在中位数跨越\(\alpha\)时确定\(a_k\)。

\[\dfrac{p_{k-2}}{q_{k-2}},\dfrac{p_{k-2}+p_{k-1}}{q_{k-2}+q_{k-1}},\dfrac{p_{k-2}+2p_{k-1}}{q_{k-2}+2q_{k-1}},\cdots,\dfrac{p_{k-2}+a_kp_{k-1}}{q_{k-2}+a_kq_{k-1}}=\dfrac{p_k}{q_k}\]

　　继续回到前面的问题，现在知道渐进分数和中位数分布在收敛值的两侧，且每侧都是单调的。每侧相邻两个分数可以表示为\(\dfrac{P(r)}{Q(r)}=\dfrac{p_kr+p_{k-1}}{q_kr+q_{k-1}}\)和\(\dfrac{P(r+1)}{Q(r+1)}\)，它们的差为\(\dfrac{1}{Q(r)Q(r+1)}\)，分子为1表明它们之间不可能有分母大于\(Q(r+1)\)的分数，否则该分数与\(\dfrac{P(r)}{Q(r)}\)的差必然大于\(\dfrac{1}{Q(r)Q(r+1)}\)。所以最佳逼近必然只能取渐进分数及其中位数，显然渐进分数必然是最佳逼近，但中位数就不一定是了，它甚至都不一定是既约分数。

　　仔细比较公式（10）和（11），（11）明显比（10）更严格，如果把公式（12）也换成较严格的条件，会发生什么呢？为区别这两种逼近，满足公式（12）的称为第一类型最佳逼近，而满足公式（13）的称为第二类型最佳逼近。第二类型的最佳逼近当然肯定也是第一类型的，反之则不一定成立，第二类型将剔除掉所有中位数，得到让我们心怡的结论。

\[\left|{m\alpha-n}\right|<\left|{m'\alpha-n'}\right|\tag{13}\]

 　　证明的重点都在于对公式（4）（9）的深度理解，相邻连分数之间再也插不进比它们分母小的分数。如果第二类型最佳逼近\(\dfrac{n}{m}\)在\(\dfrac{p_{k-1}}{q_{k-1}}\)和\(\dfrac{p_{k+1}}{q_{k+1}}\)之间，它必然在\(\dfrac{p_{k-1}}{q_{k-1}}\)和\(\dfrac{p_k}{q_k}\)之间，所以\(m>q_k\)且\(\left|{m\alpha-n}\right|<\left|{q_k\alpha-p_k}\right|<\dfrac{1}{q_{k+1}}\)。而另一方面\(\left|{\alpha-\dfrac{n}{m}}\right|\geqslant\left|{\dfrac{p_{k+1}}{q_{k+1}}-\dfrac{n}{m}}\right|\geqslant\dfrac{1}{mq_{k+1}}\)，矛盾，所以第二类型逼近只能是渐进分数。反之如果\(k>s\)，则利用误差估计（9）有\(\left|q_k\alpha-p_k\right|\leqslant\dfrac{1}{q_{k+1}}<q_s+q_{s+1}<\left|q_s\alpha-p_s\right|\)，也就是说所有渐进分数都是第二类型逼近。所以除了特殊情况\(\alpha=x.5\)外，第二类型渐进逼近和渐进分数是等价的。

　　渐进分数可以寻找最佳的有理逼近，它可以被用于齿轮制造、日历编撰等，另外还可以求对数的近似值（想想怎么算？）。

　　渐进分数是实数的逼近表示，那么局部商\(a_i\)的大小能否说明什么呢？笼统地说，它表示渐进分数离实数究竟有多近，即可以用来度量逼近。如何度量一个有理数对实数的逼近程度？研究误差和分母的关系是一个比较可行的方法，根据公式（9）有关系式（14）。这个关系式是对所有渐进分数都成立的，欲构造单个无限接近该误差的连分数是很容易的，所以该式不能被加强。该结论有两个扩展结论：（1）相邻两个渐进分数必有一个满足（15）式；（2）相邻三个渐进分数必有一个满足（16）式。而且考察\([1,1,1,\cdots]\)可知，该结论已经不能再扩展。

\[\left|{\alpha-\dfrac{p_k}{q_k}}\right|<\dfrac{1}{q_k^2}\tag{14}\]

\[\left|{\alpha-\dfrac{p_k}{q_k}}\right|<\dfrac{1}{2q_k^2}\tag{15}\]

\[\left|{\alpha-\dfrac{p_k}{q_k}}\right|<\dfrac{1}{\sqrt{5}q_k^2}\tag{16}\]

　　利用公式（9）容易得到以下估计式（17），该式说明了\(a_k\)越大，它所对应的渐进分数就“更好地”逼近连分数的值，而\([1,1,1,\cdots]\)则是最坏的数。关于逼近的度量还有很多结论，这里只是抛砖引玉，让大家有个概念，具体内容请参考相关资料。

\[\left|{\alpha-\dfrac{p_k}{q_k}}\right|<\dfrac{1}{a_{k+1}q_k^2}\tag{17}\]

　　现在来看一个逼近度量的应用，由此窥见连分数理论在高等理论中的作用。考察\(n\)次代数数\(\alpha\)，设它满足有理系数多项式\(f(x)=(x-\alpha)g(x)\)。易证\(g(\alpha)\ne 0\)，取使\(g(x)\ne 0\)的区间，并设\(\left|{g(x)}\right|>M\)。在区间上讨论\(\dfrac{p}{q}-\alpha=\dfrac{f(\dfrac{p}{q})}{g(\dfrac{p}{q})}\)，容易有\(\left|{\dfrac{p}{q}-\alpha}\right|>\dfrac{1}{Mq^n}\)。进一步讨论既有刘维尔（Liouville）定理：对\(n\)次代数数\(\alpha\)，存在正数\(C\)使得（18）式总成立。该定理指出了代数数的有理逼近性质，可以用它来轻松构造超越数（取适当\(a_k\)），刘维尔用它构造了第一个超越数\(\sum\limits_{k=1}^\infty{10^{- k!}}\)。

\[\left|{\alpha-\dfrac{p}{q}}\right|>\dfrac{C}{q^n}\tag{18}\]

4. 循环连分数

　　十进制循环小数是有理数，你可能好奇循环（periodic）连分数会有什么性质呢？首先，模仿循环小数，我们把循环连分数记作\([a_0,\cdots,a_{s-1},\dot{a}_s,a_{s+1},\cdots,\dot{a}_k]\)。对于循环连分数，在进入循环节后总有\(r_k=r_{k+l}\)，容易由归纳式得到一个二次方程，并进而知道该连分数是2次代数数。反过来，2次代数数的连分数，也必然是循环的，这个定理最初由拉格朗日证明。大概思路是考察余式的二次方程，发现它的系数有界，从而余式的个数有限，所以必然会出现循环。这里打算从另一个角度来证明这个定理，因为我们可以得到更多有趣的东西。

　　我们先从最简单的情况开始考虑，连分数\(\alpha=[\dot{a}_0,\cdots,\dot{a}_n]\)称为纯循环连分数，并记\(\beta=[\dot{a}_n,\cdots,\dot{a}_0]\)。考察由归纳公式形成的二次方程，并使用公式（8），容易证明\(\alpha\)和\(\overline{\alpha}=-\dfrac{1}{\beta}\)是同一整系数二次方程的根，它们互为共轭且满足条件（19）。容易知道二次代数数都有形式\(r+s\sqrt{D}\)，满足（19）的二次代数数称为既约的。可以证明\(\alpha\)的余式\(r_1\)也是即约的，也容易知道对某个\(D\)即约二次代数数是有限的，故必有某个余式满足\(r_k=\alpha\)，这就证明了即约二次代数数必是纯循环连分数。综合得到纯循环连分数和即约二次代数数是等价的。对于一般的二次代数数，用\(\alpha\)的表达式来表示\(r_k\)，可以证明它迟早会成为即约的，所以循环节必将出现，故循环连分数和二次代数数也是等价的。

\[\alpha>1,\quad -1<\overline{\alpha}<0\tag{19}\]

　　容易证明\(\alpha=\sqrt{D}+a_0\)是即约的（\(a_0\)为\(\sqrt{D}\)的首项），记\(\alpha=[\dot{2a}_0,\cdots,\dot{a}_n]\)。由以上结论可有\(\beta=-\dfrac{1}{\overline{\alpha}}=[\dot{a}_n,\cdots,\dot{2a}_0]\)，而\(\beta=\dfrac{1}{\alpha-2a_0}=[\dot{a}_1,\cdots,a_n,\dot{2a}_0]\)，所以\(a_1,\cdots,a_n\)对称。故有\(\alpha=[\dot{2a}_0,a_1,a_2,\cdots,a_2,\dot{a}_1]\)，进而有表达式（20）。

\[\sqrt{D}=[a_0,\dot{a}_1,a_2,\cdots,a_2,a_1,\dot{2a}_0]\tag{20}\]

 

【全篇完】