极限编程，最强N皇后JAVA解题代码，4秒出15皇后，33秒出16皇后

私人博客原文链接来自：http://www.hexcode.cn/article/4089/show

8皇后以及N皇后算法探究，回溯算法的JAVA实现，非递归，循环控制及其优化

8皇后以及N皇后算法探究，回溯算法的JAVA实现，非递归，数据结构“栈”实现

8皇后以及N皇后算法探究，回溯算法的JAVA实现，递归方案

这几天，准确来说是连续4天了

真的能称之为极限编程了

关于N皇后算法的极限挑战，最终很满意

代码使用了“一维棋盘”，“对称剪枝”，“递归回溯”，“多线程”等特色

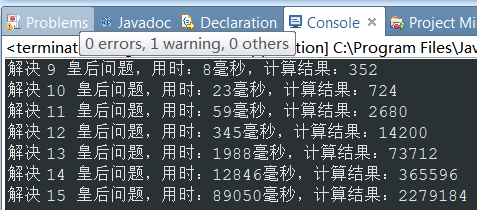
最终结果：

15皇后，用时：4903毫秒，计算结果：2279184

16皇后，用时：33265毫秒，计算结果：14772512

17皇后，用时：267460毫秒，计算结果：95815104

比起我第一天写N皇后，14皇后用时87秒的成绩，提高太多了！！！

 

说好的一定要在100秒内解16皇后，终于解脱了

啥都不说了，贴上代码和运算成绩

package  com.newflypig.eightqueen;
import  java.util.ArrayList;
import  java.util.Date;
import  java.util.List;
import  java.util.concurrent.Callable;
import  java.util.concurrent.ExecutorService;
import  java.util.concurrent.Executors;
import  java.util.concurrent.Future;


public  class  EightQueen7 {
    private  static  final  short  K= 8 ;     //使用常量来定义，方便之后解N皇后问题
    private  static  short  N= 0 ;

    public  static  void  main(String[] args)  throws  Exception {
        for (N= 9 ;N<= 17 ;N++){
            long  count= 0 ;
            Date begin = new  Date();
            /**
             * 初始化棋盘，使用一维数组存放棋盘信息
             * chess[n]=X:表示第n行X列有一个皇后
             */

            List< short []> chessList= new  ArrayList< short []>(N);
            for ( short  i= 0 ;i<N;i++){
                short  chess[]= new  short [N];
                chess[ 0 ]=i;
                chessList.add(chess);
            }

            short  taskSize =( short )( N/ 2 +(N% 2 == 1 ? 1 : 0 ) );
            // 创建一个线程池
            ExecutorService pool = Executors.newFixedThreadPool(taskSize);
            // 创建多个有返回值的任务
            List<Future<Long>> futureList =  new  ArrayList<Future<Long>>(taskSize);
            for  ( int  i =  0 ; i < taskSize; i++) {
                Callable<Long> c =  new  EightQueenThread(chessList.get(i));
                // 执行任务并获取Future对象
                Future<Long> f = pool.submit(c);
                futureList.add(f);
            }
            // 关闭线程池
            pool.shutdown();

            for ( short  i= 0 ; i<( short ) (taskSize - (N% 2 == 1 ? 1 : 0 )); i++){
                count+=futureList.get(i).get();
            }
            count=count* 2 ;
            if (N% 2 == 1 )
                count+=futureList.get(N/ 2 ).get();

            Date end = new  Date();
            System.out.println( "解决 "  +N+  "皇后问题，用时："  +String.valueOf(end.getTime()-begin.getTime())+  "毫秒，计算结果：" +count);
        }
    }
}

class  EightQueenThread  implements  Callable<Long>{
    private  short [] chess;
    private  short  N;

    public  EightQueenThread( short [] chess){
        this .chess=chess;
        this .N=( short ) chess.length;
    }


    @Override
    public  Long call()  throws  Exception {
        return  putQueenAtRow(chess, ( short ) 1 ) ;
    }


    private  Long putQueenAtRow( short [] chess,  short  row) {
        if (row==N){
            return  ( long )  1 ;
        }

        short [] chessTemp=chess.clone();
        long  sum= 0 ;
        /**
         * 向这一行的每一个位置尝试排放皇后
         * 然后检测状态，如果安全则继续执行递归函数摆放下一行皇后
         */
        for ( short  i= 0 ;i<N;i++){
            //摆放这一行的皇后
            chessTemp[row]=i;

            if ( isSafety( chessTemp,row,i) ){
                sum+=putQueenAtRow(chessTemp,( short ) (row+ 1 ));
            }
        }

        return  sum;
    }

    private  static  boolean  isSafety( short [] chess, short  row, short  col) {
        //判断中上、左上、右上是否安全
        short  step= 1 ;
        for ( short  i=( short ) (row- 1 );i>= 0 ;i--){
            if (chess[i]==col)   //中上
                return  false ;
            if (chess[i]==col-step)  //左上
                return  false ;
            if (chess[i]==col+step)  //右上
                return  false ;

            step++;
        }

        return  true ;
    }
}

 

 

这是四天前的成绩：

 

确实有了很大的提升！