信息安全系统设计基础第三周学习总结
信息安全系统设计基础第三周学习总结
【教材第二章:信息的表示和处理】
【学习时间:12小时】
一、教材知识点
1.无符号数、有符号数(2进制补码)、浮点数,从逆向角度考虑为什么会产生漏洞?
【任何漏洞产生都必然因为系统不可更改的局限性——>无符号数、有符号数、浮点数的局限性——>无符号数或者有符号数的表示范围有限,而浮点数虽然编码范围大,但是不精确】
2.在C语言中,所有以0X或者0x开头的数字常量都常被认为是十六进制的值
3.计算机的字长指明的最重要的系统参数是虚拟地址空间的最大大小(字长为w,则程序最多访问2^w个字节)
4.gcc -m32 可以在64位机上生成32位的代码
5.字节顺序的两种表示方法:小端是“高对高、低对低”,大端与之相反
6.代码执行
#include <stdio.h>
typedef unsigned char *byte_pointer;
void show_bytes(byte_pointer start, int len)
{
int i;
for(i = 0;i<len;i++)
{
printf("%.2x",start[i]);
}
printf("\n");
}
void show_int(int x)
{
show_bytes((byte_pointer) &x, sizeof(int));
}
void show_float(float x)
{
show_bytes((byte_pointer) &x, sizeof(float));
}
void show_pointer(void *x)
{
show_bytes((byte_pointer) &x, sizeof(void *));
}
void test_show_bytes(int val)
{
int ival = val;
float fval = (float)ival;
int *pval = &ival;
show_int(ival);
show_float(fval);
show_pointer(pval);
}
void main()
{
int val;
printf("please enter an int:\n");
scanf("%d",&val);
test_show_bytes(val);
}
以12345为例,输出结果如下:
(图1)
说明,该笔记本(yoga2)为小端法机器。同时,还了解到,不同的机器或者操作系统使用不同的存储分配原则。
7.文本数据比二进制数据具有更好的平台适应性。
8.只要一个与非门,就可以完成所有的逻辑运算。
9.要用C99中的“long long”类型,编译是要用 gcc -std=c99
10.B2T中,最高位权重为-2^(w-1)。这也可以解释,利用补码可以把数学运算统一成加法
11.将有符号数强转成无符号数之后,数字的数值发生改变,然而其位表示不变。(如,将-12345的补码看作无符号数字的话,则为53191.经过类型强转得到的结果也是53191)
12.T2Uw(x)=x+2^w,x<0;U2Tw(x) = x-2^w,x>=2^(w-1)
13.几乎所有的机器都使用补码;通常,大多数数字都默认为有符号.然而,在一个运算式中,如果有一个参数是无符号的 ,那么另外一个也会默认为无符号数
14.怎么样让负数等于正数?由练习题2.21可以得到一些启示:在负数x后加上U,可以使其转换为(2^w+x)
15.零扩展类似于逻辑左(右)移。即:将一个无符号数转换为一个更大的数据类型,简单地在前面加上0。符号扩展类似于算数左(右)移。即:将一个补码数字转换为一个更大的数据类型,在表示中添加最高有效位值得副本。注意:在进行数据大小、有无符号的转换时;如果要进行从short到unsigned的转换,必须经过short->int->unsigned
16.数字截断:将一个w位的数丢弃前k位得到的数字(二进制)为:2^w mod 2^k,有可能发生溢出.
17.算数运算的溢出,是指完整的整数结果不能放到数据类型的字长限制中去。比如,两个数的和为2^w或者更大时,就发生了溢出。
18.补码的非:除了x=-2^(w-1)和0的非是他们本身之外,其他数字的非(加法逆元)都可以通过2^w-x获得。
19.C语言中,有符号数字的乘法是通过将2w位截断为w位的方式来实现的。即:xy - U2T((xy)mod 2 ^w)
20.表达式x*K,其中,K可以表示为一组从位位置n到m连续的1和其他位置的0,那么,表达式可以表示为:
A:(x<<n)+(x<<n-1)+……+(x<<m) B:(x<<n+1)-(x<<m)
21.除以2的幂可以用移位运算实现(右移)。事实证明,移位总是摄入到0,这一结果与整数除法的规则一样。对于非负数,算术右移和逻辑右移都可以作为除法运算;而负数则是进行算术右移。
22.浮点数对形如V = X*2^Y的数字进行编码,主要是很接近于0或者很大的数字。当一个数字不能被精确地表示为这种形式时,就必须要向上或者向下调整,即为舍入。
23.IEEE浮点标准——用V= (-1)^sM2^E来编码一个数。其中:
符号:s决定这个数是负数(s=1)还是正数(s=0),对于数值是0的符号位解释为特殊情况。 尾数:M是一个二进制小数 阶码:E对浮点数加权,可以是负数
根据以上,float:s=1位,exp=8位,frac=23位
double:s=1位,exp=11位,frac=52位
24.整数与浮点数表示同一个数字的关系?
整数与浮点数表示同一个数字时,化成二进制形式之后,可以看到,整数等于1 的最高有效位之后的数字,与浮点数小数部分的高位是相匹配的。
25.整数与浮点数转换规则?
整数->浮点数:整数转换成二进制表示,然后小数点左移若干位得到规格化表示;取出小数部分的数值,在后面补0使其达到23位; 用frac加上偏置量得到的结果用二进制表示,放在取出的部分前面,再加上一个符号位即可。
26.利用这一特性:x/y = (x+y-1)/y。在移位(除法)之前“偏置”这个值,通过这种方法修正不合理的输入。
27.在IEEE浮点数表示中,以规格化表示的阶码字是以偏置形式表示的有符号数。
28.当阶码全为1、小数域全为0时,得到的值表示无穷;当阶码全为1、小数域不全为0时,结果是NaN(not a number)
二、课本练习题筛选
1.
0x503c+0x8 = 0x5044
0x503c-0x40 = 0x4ffc
0x503c+64 = 0x5070(原始答案错误。原因:未看到64前面没有十六进制标识)
2.写出0x00359141、0x4a564504的二进制表示。并移动相对位置使其尽量匹配
0x00359141 = 0000 0000 0011 0101 1001 0001 0100 0001(2进制)
0x4a564504 = 0100 1010 0101 0110 0100 0101 0000 0100(2进制)
0000 0000 001101011001000101000001
*************************
0100 1010 010101100100010100000100
共有21位相匹配。整数基本上所有有效位都嵌在浮点数中。
3.a = [01101001],b = [01010101]。计算:
~a = [10010110]
~b = [10101010]
a&b = [01000001]
a |b = [01111101]
a^b = [00111100]
4.写一段代码实现一个数组的头尾元素依次交换
代码如下:
#include<stdio.h>
#define MAX 10
void inplace_swap(int *x,int *y)
{
*y = *x^*y;
*x = *x^*y;
*y = *x^*y;
}
void reverse_array(int a[], int cnt)
{
int first,last;
for(first = 0,last = cnt-1;first<=last;first++,last--)
inplace_swap(&a[first], &a[last]);
}
void main()
{
int a[MAX];
int count,i;
printf("please enter the amount of numbers( no more than %d):\n",MAX);
scanf("%d",&count);
printf("please enter numbers('e' as the end)\n");
for(i = 1;i<=count;i++)
{
scanf("%d\n",&a[i-1]);
}
printf("the original array is as follow:\n");
for(i = 1;i<=count;i++)
{
printf("%d ",a[i-1]);
}
reverse_array(a, count);
printf("the new array is as follow:\n");
for(i = 1;i<=count;i++)
{
printf("%d ",a[i-1]);
}
}
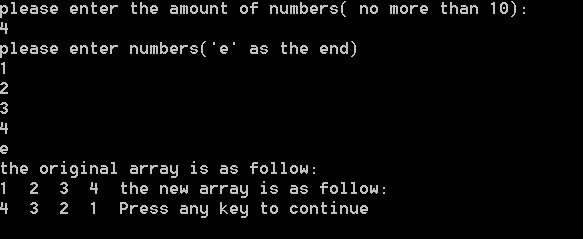
这段代码分别以1,2,3,4和1,2,3,4,5作为输入的时候,结果如下:
(图2)
(图3)
即:当数组长度为奇数的时候,输出的结果最中间的数字变为0.原因?在最后一次调用inplace_swap的时候,传入的first和last都是原数组中最中间的数字;在第一处*y = x^y时,y指向的数字就变为了0.此后,0变作为最中间的数字参与循环。解决办法?将循环条件中的first<=last 改为first<last(最中间的数字不会参与循环)即可。
5.假设有两个函数实现位设置bis和位清除bic操作;只利用这两个函数实现按位 | 和^操作。
int bis(int x, int y);
int bis(int x, int y);
int bool_or(int x,int y)
{
int result = bis(x,y);
return result;
}
int bool_xor(int x,int y)
{
int result = bis(bic(x,y),bic(y,x));
return result;
}
本题初始解答错位。原因?未掌握 x^y = (x&~y) | (~x&y)
6.假设x,y的字节值分别是0x66,0x39,求:
x & y = 0x20
x | y = 0x7f
~x | ~y = 0xdf
x&!y = 0x00
x && y = 0x01
x || y = 0x01
!x || !y = 0x00
7.对于32位补码形式显示的十六进制值,转化为十进制
0x1b8 = 110
0xfffffe58 = -424
8.
T2TU4(-8) = 8 T2U4(-3) = 13 T2U(-2) = 14 T2U4(0) = 0
9.假设在运用补码运算32位机器上对以下这些表达式求值
-2147483647-1 == 2147483648U 无符号 1 -2147483647-1<2147483647 有符号 1 -2147483647-1U <2147483647 无符号 0 -2147483647-1U <-2147483647 无符号 1
10.假设在一个采用补码运算的32位机器上执行这些函数。计算下列输入参数之后的结果:
#include<stdio.h>
int fun1(unsigned word)
{
return (int)((word<<24)>>24);
}
int fun2(unsigned word)
{
return ((int)word<<24)>>24;
}
void main()
{
int word;
printf("please enter a number:\n");
scanf("%d",&word);
printf("the result of fun1:%d\n",fun1(word));
printf("the result of fun2:%d\n",fun2(word));
}
分析:fun1()是将word进行过逻辑左移和右移的结果转换为int型;而fun2()是将word先强制转换为int型,随后进行的算数左移和右移
w:0x00000076 fun1(w)=0x00000076,fun2(w)=0x00000076
w:0x87654321 fun1(w)=0x00000021,fun2(W)=0x00000021 (此处起初和答案有冲突。最初认为在fun2()中,w转换为的int型应该表示的是一个负数,所以逻辑移动时应该补1.后来意识到,是先进行左移即右侧六个十六进制位补f,随后右移的时候,因为最高有效位是0,所以前侧六个十六进制位补0)
w:0x000000c9 fun1(w)=0x000000c9 fun2(w)=0xffffffc9
11.假设将一个4位数值(0——f)截断为一个3位数值(0——7),填写截断后的结果。
原始值:0 无符号截断值:0 补码截断值:0
原始值:2 无符号截断值:2 补码截断值:2
原始值:9 无符号截断值:1
原始值:b 无符号截断值:3
原始值:15 无符号截断值:7
原始值:-7 补码截断值:1
原始值:-1 补码截断值:-1
12.以下代码试图计算数组a[]中所有元素的和,然而当参数length=0时,会发生存储器错误。试解释原因并修改代码。
#include<stdio.h>
#define MAX 100
float sum_elements(float a[], unsigned length)
{
int i;
float result = 0;
for (i =0;i<=length-1;i++)
{
result+=a[i];
}
return result;
}
void main()
{
float a[MAX];
unsigned number;
int i;
printf("Please enter the amount of numbers in your array:\n");
scanf("%u",&number);
if(number <0)
{
printf("Wrong!\n");
return;
}
if(number == 0)
{
printf("the result is:%f\n",sum_elements(a, number));
return;
}
else
{
printf("Please enter the elements:(the tail of array should be end by 'e')\n");
for(i = 0;i<=number-1;i++)
{
scanf("%f\n",&a[i]);
}
printf("the result is:%f\n",sum_elements(a, number));
return;
}
}
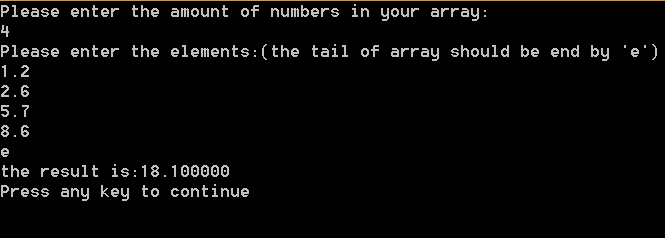
以正常的浮点数数组{1.2,2.6,5.7,8.6}作为输入,得到正常结果:
(图5)
如果以length=0输入,结果如下
(图6)
解释:原因应该在“i<=length-1”与之前声明的“unsigned length”的矛盾中。因为当输入的length是0时,length-1=0-1(无符号数运算),即模数加法,得到的是Umax。而任何数都是小于Umax的,所以比较式恒为真。则循环会访问数组a中的非法元素。简单的处理办法就是将length声明为int型。
13.任务:写一个函数判定一个字符串是否比另一个更长。函数如下:
size_t strlen(const char *s);
int strlonger(char *s,char *t)
{
return strlen(s)-strlen(t) >0;
}
在什么情况下会产生不正确的结果?
当s的长度小于t的长度时,strlen(s)-strlen(t) 仍然以无符号数进行运算,则会产生模数加法,使其恒大于零。
如何修改代码?
把return strlen(s)-strlen(t) >0改成return strlen(s)>strlen(t)即可。
14.写一个具有如下原型的函数:
int uadd_ok(unsigned x,unsigned y)
当x和y的和不发生溢出时,返回1
答: int uadd_ok(unsigned x,unsigned y)
{
unsigned sum = x+y;
return sum >=x;
}`
因为机器运算能力的有限性,不可能使用x+y>2^w这样的判断语句。所以通过判断两数之和是否大于某一个被加数这样的间接方式确定。
15.计算下列16进制数字的加法逆元。
F 十进制:15 逆元:1 0 十进制:0 逆元:0
16.求:
无符号:x=[100],y=[101] xy = 010100=20,截断后的xy= 100=4
有符号:x=[100],y=[101] xy = 001100=12,截断后的xy= 100=-4 (初始解答:x=[100],y=[101] xy = 10100=-12,截断后的xy= 100=-4。错误。因为:有符号的补码运算,如果运算数有负数,应该把正确结果转换成二进制)
17.对于位位置n为有效位的情况,我们要怎么样修改表达式B:(x<<n+1)-(x<<m)?
表达式变为了-(x<<m)。解析(不同于课本):n为有效位,则K为补码表示的负数,将其(认为K的二进制表示中只有n到m位是1,其余位是0)转换为二进制的绝对值形式后,发现其二进制表示中只有第m位是1,其余位都是0。那么,x*k就变成了-(x<<m)
18.写一个函数div16,对任何整数参数,返回x/16的值。不能使用四则运算和任何条件运算符、比较运算符。(假设你的机器是32位,使用补码表示,右移都是算术右移)
(分析:正整数的除法运算很容易就通过>>4移位实现,然而还需要考虑负数的情况。如果不能使用条件语句,就要写出满足正负数的通用公式。)
int div16(int x)
{
int bias = (x>>31)&0xf;//如果是负数,bias就会变成f
return (x+bias)>>4;
}
19.在下面的代码中,我们定义了常数M和N
#define M
#define N
int arith(int x,int y)
{
int result = 0;
result = x*M+y/N;
return result;
}
以下是将机器代码翻译为C语言的结果:
int optarith(int x,int y)
{
int t = x;
x<<5;
x-=t;
if(y<0) y+=7;
y>>3;
return x+y
}
问:M和N是多少? 1.x左移五位即乘32,减去1之后相当于乘31;则M=31
2.y右移三位相当于除以8;则N=8
20.假设我们对有符号数字使用补码运算。变量的初始化和声明如下:
int x = foo();
int y = bar();
unsigned ux = x;
unsigned uy = y;
对下面每个表达式,证明其真假。
1)x*x >=0 假。可以x = 65535为例;此时,按照有符号数乘法,得到的数转换为二进制之后为0xFFFE001,为负数。
2)x~y+uxuy ==-x 真。~y等于-y-1,uxuy == xy。因此,等式左右两边等价。
三、问题总结
1.P63:
通过类似的推理,我们可以得出,对于一个位模式为[x(w-1),x(w-2),……,0,……,0]的补码数x,以及在0<=k<=w范围内的任一k,位模式为[x(w-k-1),x(w-k-2),……,0,……,0]就是x*2^k的补码表示
为什么截断前面的k位、后面补上0之后,就是一个乘式结果的补码表示?
P66练习题2.42
写一个函数div16,对任何整数参数,返回x/16的值。不能使用四则运算和任何条件运算符、比较运算符。(假设你的机器是32位,使用补码表示,右移都是算术右移)
int div16(int x)
{
int bias = (x>>31)&0xf;//如果是负数,bias就会变成f
return (x+bias)>>4;
}
不太理解如何证明负数运算时,加上bias(即f)之后就可以直接右移四位?
P67练习题2.44
E.x>0||-x>0
假。设x=-2147483648(Tmin32),则x和-x都为负数
如何判断x的相反数是多少?
四、学习心得
通过本次“边读书,边思考,边记录”的过程,我深刻地意识到“精读”背后要多付出的精力、时间,更体会到与泛读甚至浏览完全不在同一个层次上的收获。第二章一共60页,坚持每一页的每一句话(不能保证是每一个字)都看到心里去,说不乏味不疲倦是不可能的。在十一假期里,我用了四天的时间,每天都看上几十页,积少成多地去读书。然而,时间上的持久带来了短期记忆模糊的问题。这时候,靠自己的笔记就可以有效地弥补记忆上的模糊,让知识点和代码“夯实”在脑子里。
这样的收获是显著的;我开始跟随老师所提出的要点去走,跟着书中的思路去走,书中所提到的引用与老师所提到的要点就好像路标,我看到了所有的路标之后,路就变得格外好走。