温控算法的实现:四
时至今日,我终于算是大体上完成了温控的算法,现在就将具体的实现总结如下。
一:matlab的仿真。
matlab可以用来实现离散PID的模拟仿真,从而用来整定最后的参数。
(1)matlab温升曲线的拟合
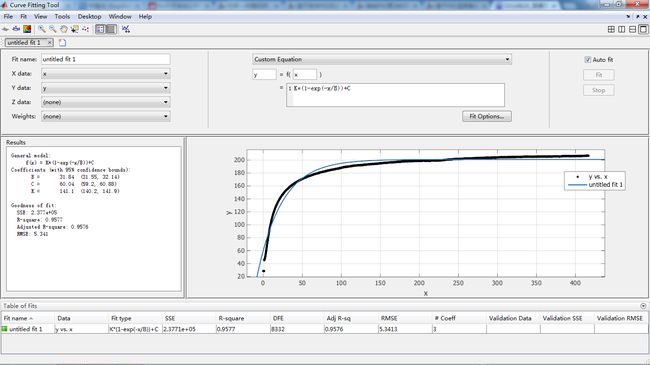
当满功率加热时,温度上升拟合的曲线如下所示:
所以由拟合结果可知,K=141.1 B=38 C=60.04
但是实际上温度的起点约为20℃,而温度的终点差不多为210℃,所以我们可以大体上以传递方程
200/38*s+1作为拟合的方程。
(2)临界比例法整定PID参数
在闭环控制系统里,将调节器置于纯比例作用下,从小到大逐渐改变调节器的比例系数,得到等幅振荡的过渡过程。此时的比例系数称为临界比例系数,相邻两个波峰间的时间间隔,称为临界振荡周期Tu。
临界比例度法步骤:
1、将调节器的积分时间置于最大(Ti = ∞),微分时间置零(Td = 0),比例系数适当,平衡操作一段时间,把系统投入自动运行。
2、将比例系数逐渐增大,得到等幅振荡过程,记下临界比例系数Ku和临界振荡周期Tu值。
3、根据和值,采用经验公式,计算出调节器各个参数,即Ti和Td的值。
经验公式为:
Ts = 0.14 * Tu Kp = 0.63 * Ku Ti = 0.49 * Tu Td = 0.14 * Tu
(3)matlab得到Ku和Tu
function PID_1(M)
% M为输出图形的横坐标最大值;
ts=0.05;%采样时间 50ms
G=tf(200,[38,1])
Gd=c2d(G,ts,'z') %Z变换
[num,den]=tfdata(Gd,'v')
c_1=0;
y_1=0;
e_1=0;e_2=0;
kp=7.6;Ti=inf;Td=0;
ki=kp*ts/Ti;
kd=kp*Td/ts;
A=kp*(1+ts/Ti+Td/ts);
B=-kp*(1+2*Td/ts);
C=kp*Td/ts;
for k=1:1:M*20
t(k)=k*ts;
r(k)=1;
y(k) = -den(2)*y_1 + num(2)*c_1 ;
e(k) = r(k) - y(k);
c(k) = (A*e(k) + B*e_1 + C*e_2);
c(k) = c_1 + c(k);
c_1 = c(k);
y_1 = y(k);
e_2 = e_1;
e_1 = e(k);
end
plot(t,y,'r',t,r,'b')
grid on;
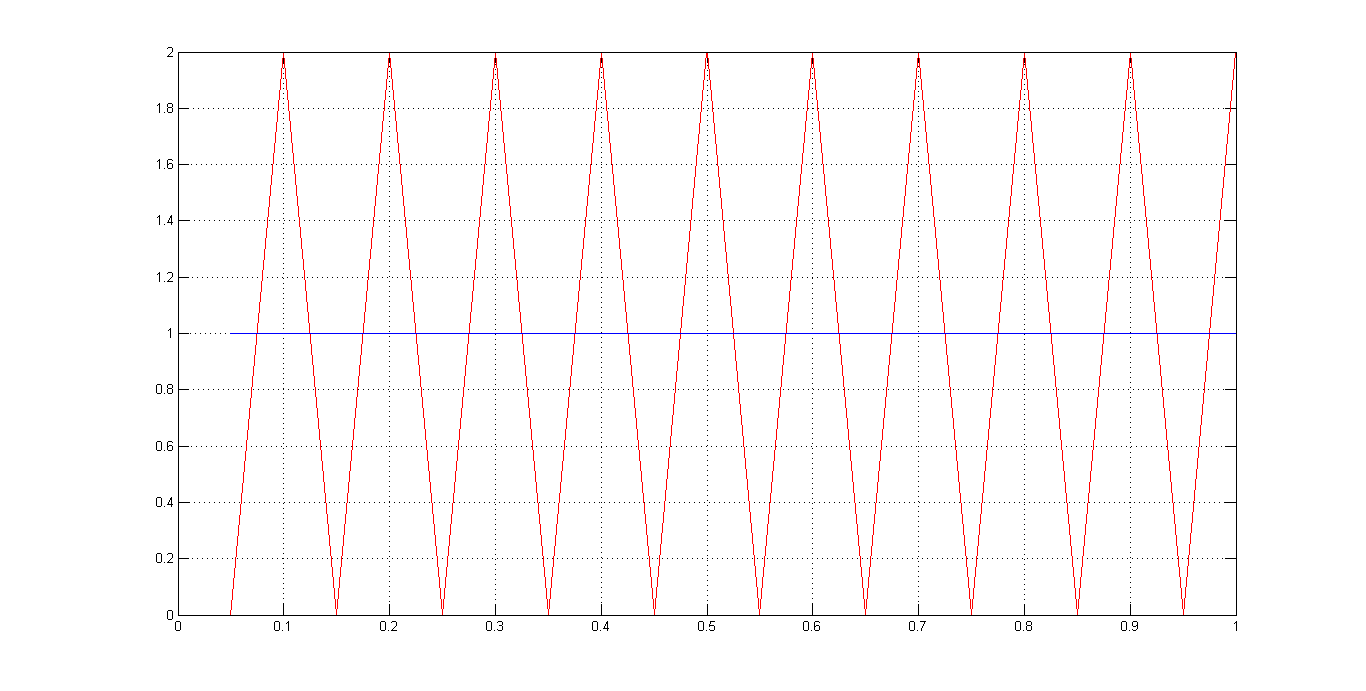
得到等幅震荡
所以可知Tu = 100ms Ku = 7.6 。
(4)确定Kp ,Ti ,Tu。
由经验公式可知,Ts = 0.14 * Tu = 14ms , Kp = 0.63 * 7.6 = 4.788 , Ti = 0.49 * Tu = 49ms
Td = 0.14 * Tu = 14ms
所以仿真
function PID_1(M)
%a选则输入信号,M为输出图形的横坐标最大值;
ts=0.014;%采样时间 50ms
G=tf(200,[38,1])
Gd=c2d(G,ts,'z') %Z变换
[num,den]=tfdata(Gd,'v')
c_1=0;
y_1=0;
e_1=0;e_2=0;
kp=4.788;Ti=0.049;Td=0.014;
ki=kp*ts/Ti;
kd=kp*Td/ts;
A=kp*(1+ts/Ti+Td/ts);
B=-kp*(1+2*Td/ts);
C=kp*Td/ts;
for k=1:1:M*71
t(k)=k*ts;
r(k)=100;
y(k) = -den(2)*y_1 + num(2)*c_1 ;
e(k) = r(k) - y(k);
c(k) = (A*e(k) + B*e_1 + C*e_2);
c(k) = c_1 + c(k);
c_1 = c(k);
y_1 = y(k);
e_2 = e_1;
e_1 = e(k);
end
plot(t,y,'r',t,r,'b')
plot(t,c,'r')
grid on;
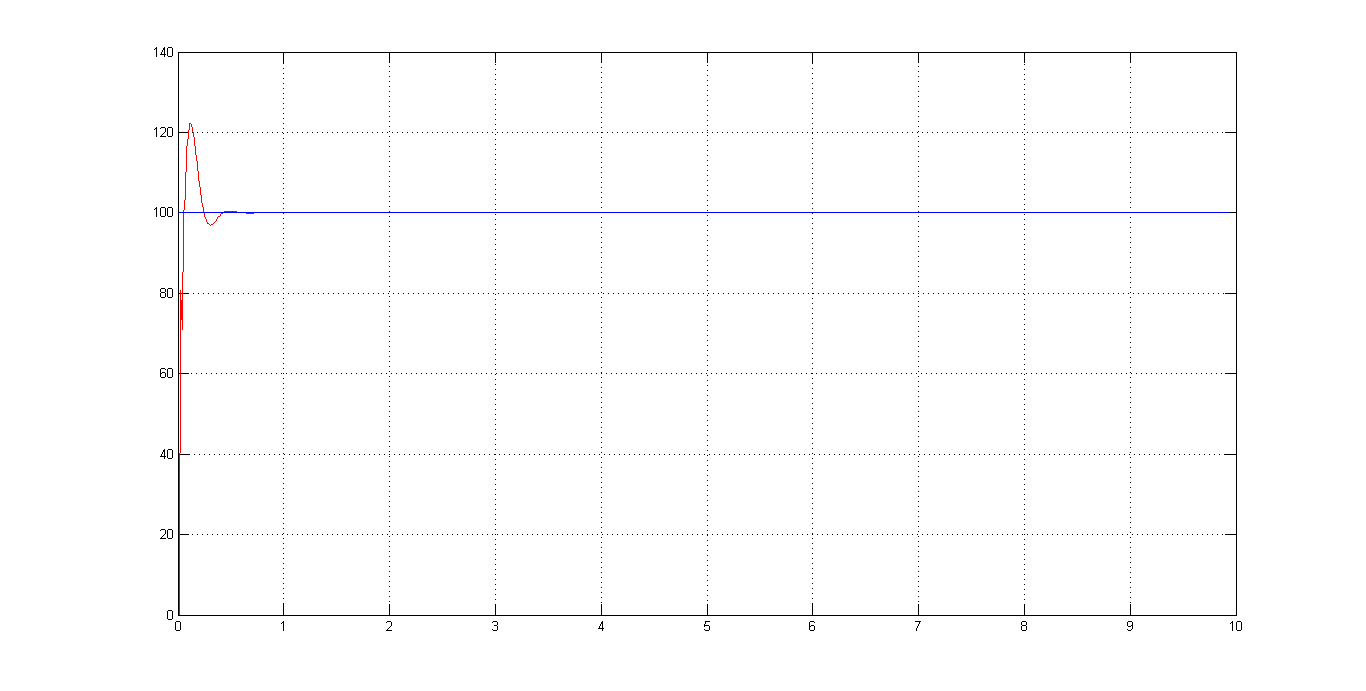
仿真结果为
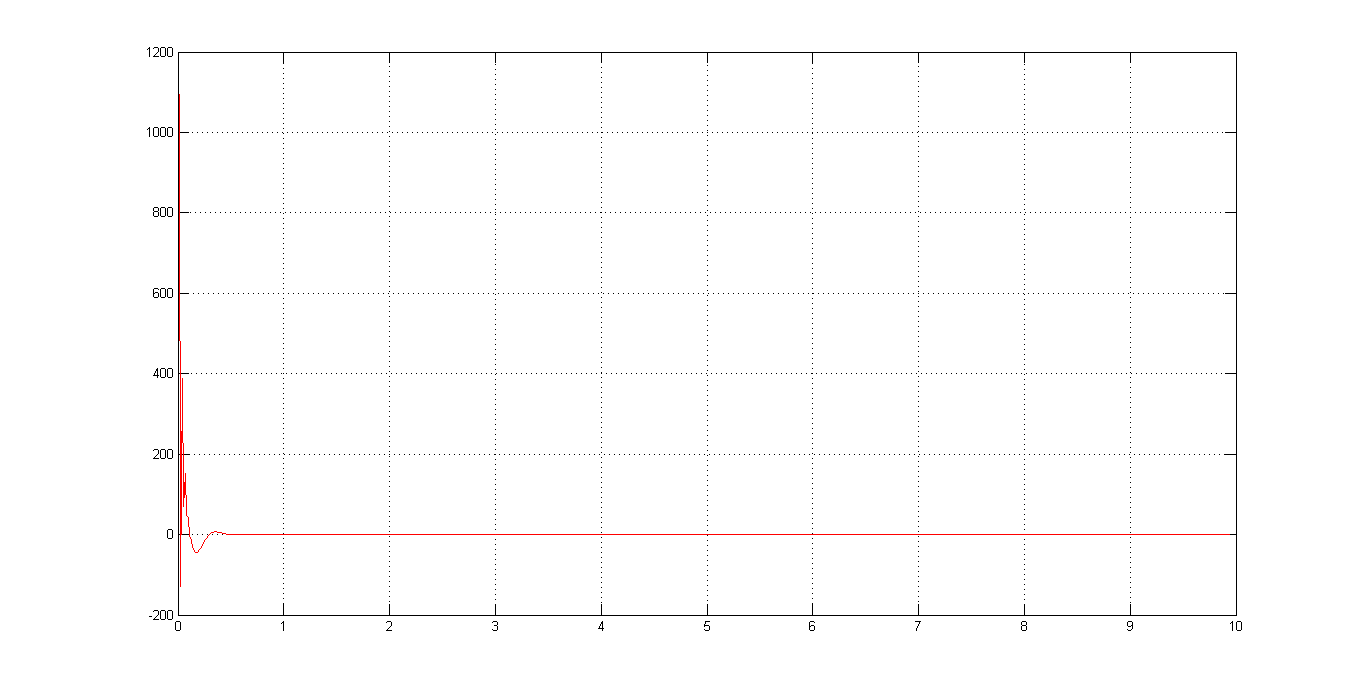
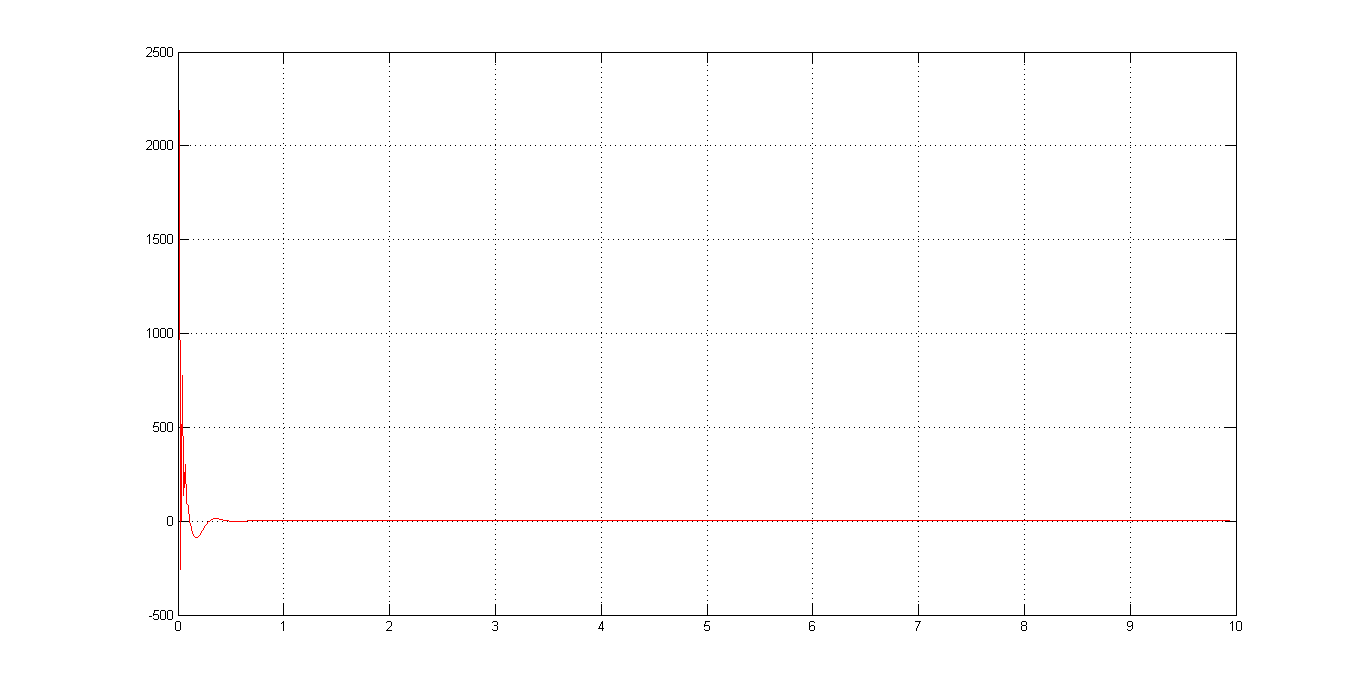
右图为变量c的仿真结果,在实际中对应着PWM波的占空比,由图中可以知道,这个数值远大于1,所以需要归一化。
那么可以在程序中设置一个幅值为200的阶跃信号,得到的c曲线为:
c_max < 2500, 所以可以设置系数为 0.0004。
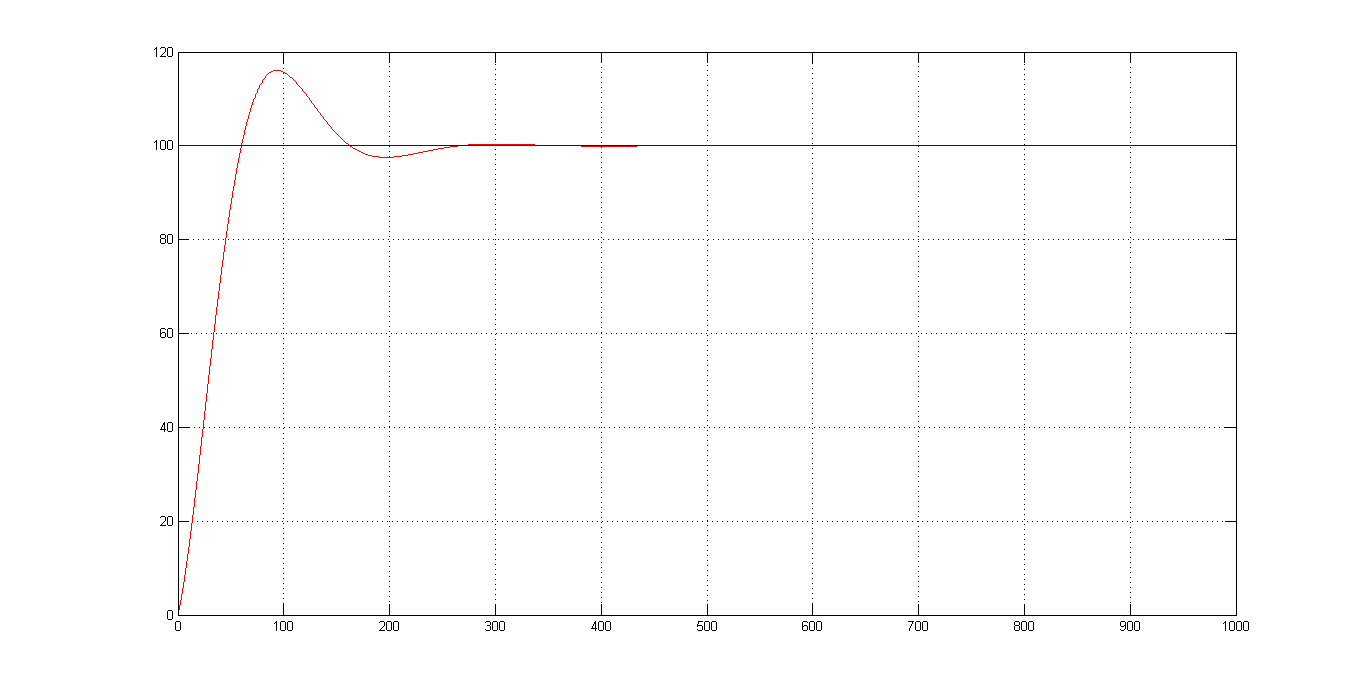
最后再经过调整,可以将Ti设置为8s , Td设置为14ms , Kp设置为4.788 。此时仿真结果为
r(k) = 100
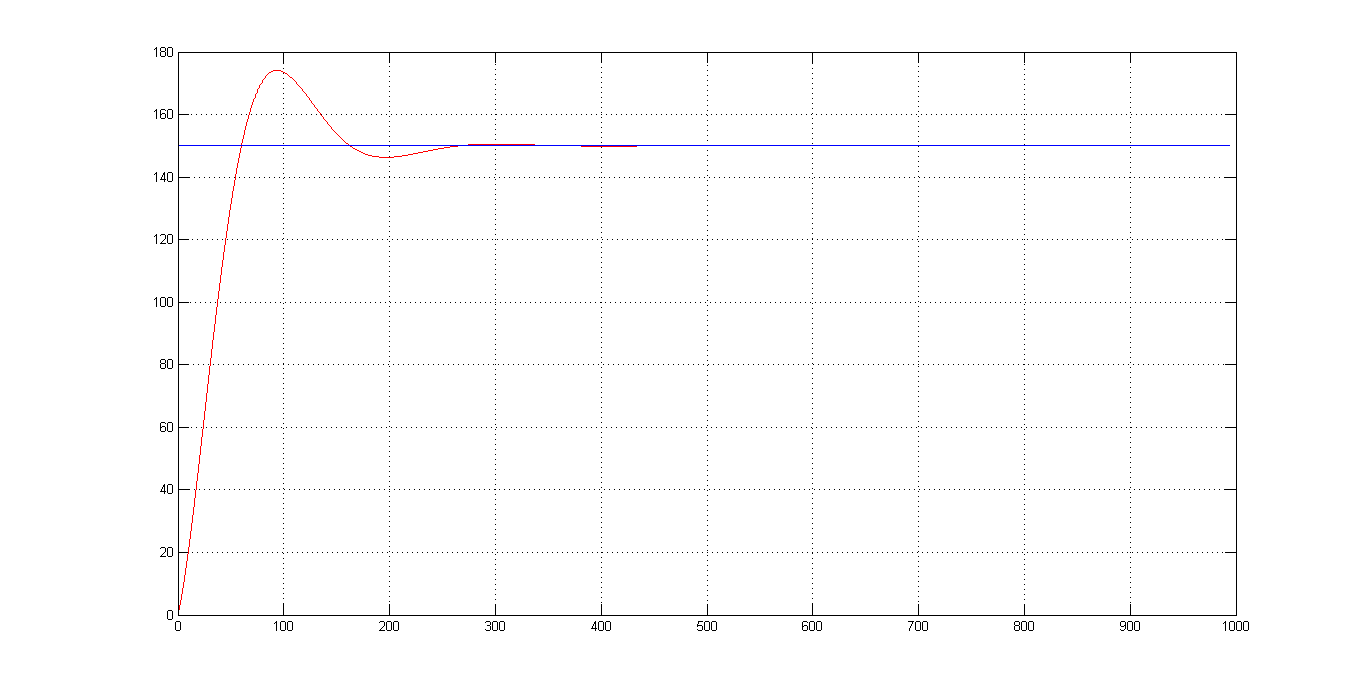
r(k) = 150
所以Kp= 4.788 Ki = Kp * Ts / Ti = 0.00839 Kd = Kp * Td / Ts = 4.788
二: 实际验证
将以上参数写入单片机中,采集温度数据,观测温升曲线,然后调试,修改各参数。
最后 将Kp,Kd修正为15,Ki修正为0.2635。比例因子修正为为0.00005,这样可以得到较好的温控效果 。
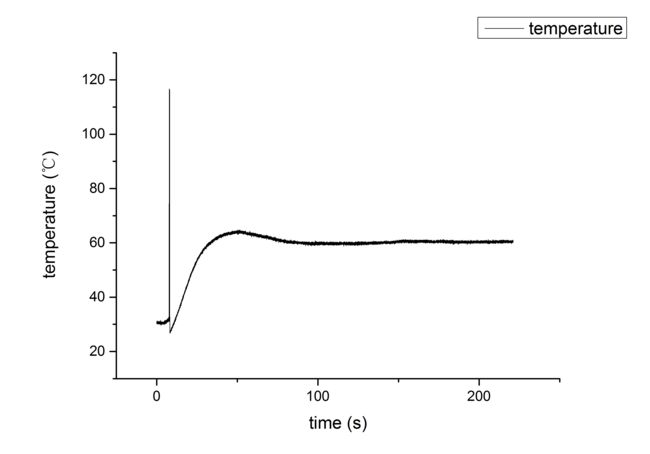
温度控制效果如下所示:
(1)温度设置为60℃时:
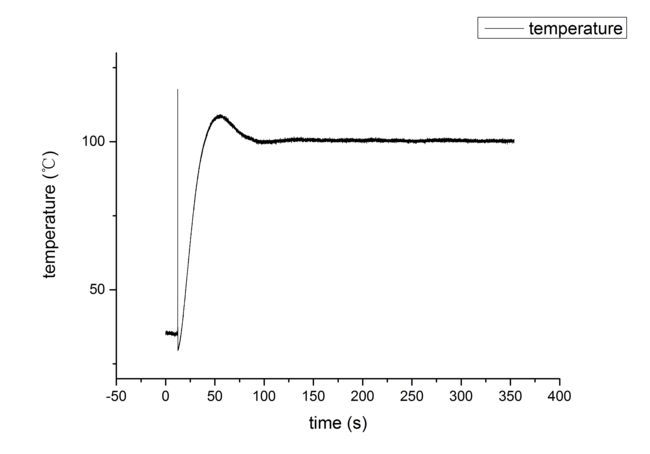
(2)温度设置为100℃时:
(3)温度设置为150℃时
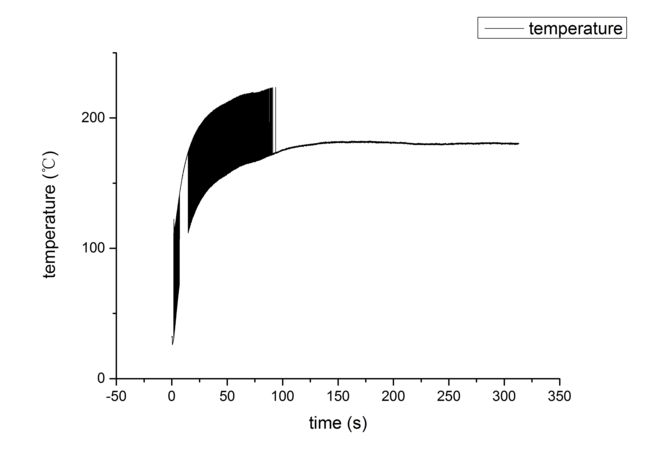
(4)设置温度为180℃时
由上述的测量数据可知,此系统可以2分钟实现温度稳定,稳定误差约为±0.5℃。