寒假集训日志（六）——ＤＰ

（一）数位DP

1057. Amount of Degrees

Time limit: 1.0 second
Memory limit: 64 MB

Create a code to determine the amount of integers, lying in the set [ X; Y] and being a sum of exactly K different integer degrees of B.

Example. Let X=15, Y=20, K=2, B=2. By this example 3 numbers are the sum of exactly two integer degrees of number 2:

17 = 2 ⁴+2 ⁰,
18 = 2 ⁴+2 ¹,
20 = 2 ⁴+2 ².

Input

The first line of input contains integers X and Y, separated with a space (1 ≤  X ≤  Y ≤ 2 ³¹−1). The next two lines contain integers K and B (1 ≤  K ≤ 20; 2 ≤  B ≤ 10).

Output

Output should contain a single integer — the amount of integers, lying between X and Y, being a sum of exactly K different integer degrees of B.

Sample

input	output
15 20 2 2	3

一道据说比较经典的题目，基本弄懂，ans++ 那里实在没搞懂，不过也没那么多时间给我犹豫。。

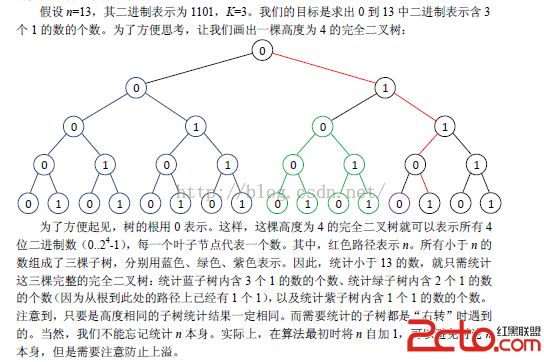
主要借助一个状态转移方程 f[i][j] = f[i-1][j-1] + f[i-1][j]

f[i][j] 表示二进制中前ｉ位中有ｊ个１的个数，其他进制的数在转换过来之后都可一借用f[i][j]来解决。可以借助这个图理解一下这个方程。

不过ａｎｓ＋＋那里实在每看懂。

 

#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<iomanip>
#include<fstream>
#include<vector>
typedef long long LL;
using namespace std;

const int maxN = 50;
int f[maxN][maxN];

void getMap (){
    f[0][ 0] = 1;
    for( int i = 1 ; i< maxN ;++i){
        f[i][0] = 1;
        for( int j=  1 ; j<=i ;++j)
            f[i][j] = f[i-1][j] + f[i-1][j-1] ;
    }
}

int solve ( int x, int k ,  int c) {
    vector< int > arr;
    while( x) {
        arr.push_back ( x% c);
        x /= c;
    }
    int ans = 0, cnt = 0  ;
    for( int i = arr.size() -1 ; i>= 0 ; --i){
        if( arr[i] == 1){
            ans += f[i][ k - cnt];
            cnt++ ;
            if( cnt == k )  break;
        }
        else if( arr[i] > 1){
            ans += f[i+1][k - cnt];
            break;
        }
    }
    if( cnt == k )  ans ++;
    return ans ;
}

int main()
{
    for( int i = 0 ; i< maxN ; ++i)
        for( int j = 0 ; j< maxN; ++j)
                f[i][j] =  0 ;
    int x, y ;
    int k, b;
    getMap();
    cin>>x>>y>>k>>b;
    cout<<solve(y,k,b) - solve(x-1 , k , b)<<endl;
return 0;
}

 

A - 数位DP

Time Limit:1000MS     Memory Limit:65536KB     64bit IO Format:%I64d & %I64u

Submit Status

Description

The counter-terrorists found a time bomb in the dust. But this time the terrorists improve on the time bomb. The number sequence of the time bomb counts from 1 to N. If the current number sequence includes the sub-sequence "49", the power of the blast would add one point.
Now the counter-terrorist knows the number N. They want to know the final points of the power. Can you help them?

 

Input

The first line of input consists of an integer T (1 <= T <= 10000), indicating the number of test cases. For each test case, there will be an integer N (1 <= N <= 2^63-1) as the description.

The input terminates by end of file marker.

 

Output

For each test case, output an integer indicating the final points of the power.

 

Sample Input

3 1 50 500

 

Sample Output

0 1 15

Hint

From 1 to 500, the numbers that include the sub-sequence "49" are "49","149","249","349",
"449","490","491","492","493","494","495","496","497","498","499", so the answer is 15. 

//也是一道很经典的题目，但是有个坑一定要注意一下，就是以防止出现４９结尾的情况
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<vector>
#include<cstring>

using namespace std;
typedef long long LL;

const int maxN = 22;
LL dp[maxN][3];

void init(){
    for( int i = 0 ; i<=maxN ;++i)
        for( int j = 0 ;j<= maxN; ++j)
            dp[i][j] = 0;
    dp[0][0] = 1;
    for(int i = 1;i<=22;i++)
    {
        dp[i][0] = dp[i-1][0]*10-dp[i-1][1];
        dp[i][1] = dp[i-1][0];
        dp[i][2] = dp[i-1][2]*10+dp[i-1][1];
    }
}

LL solve( LL x){
    int arr[maxN] ;
    memset( arr, 0 , sizeof(arr));
    int len = 0;
    while( x){
        arr[ ++ len]  = x%10;
        x /= 10;
    }
    arr[ len + 1] = 0;
    LL ans = 0, flag = 0;
    for( int i = len ; i>=1 ; --i){
        if( flag) ans += (dp[i-1][0] + dp[i-1][2])* arr[i];
        else if(arr[i] >=5)
            ans += dp[i-1][1] + dp[i-1][2]* arr[i];
        else ans += dp[i-1][2]*arr[i];
        if( arr[i+1] == 4 && arr[i] == 9 )  flag = 1;
    }
    return ans ;
}

int main(){
    int T ;
    cin>>T;
    init();
    while(T--){
        LL n;
        scanf("%lld", &n);
        LL ans ;
        ans = solve(n+1);//因为ｆｌａｇ有延迟，所以需要加１
        printf("%lld\n", ans);
    }
    return 0;
}

 

（二）树形DP