深入理解动态规划的一系列问题(8)
最优二叉搜索树问题(Optimal Binary Search Tree Problem (BST))是算导上又一个经典例题,给定一系列数据项X={x0,x1,…,x(n-1)},每项都有一个访问概率p(xi),目标是构建一棵二叉搜索树使得访问每个节点的成本最小,即Σ(p(xi) * level(xi))最小,而level(xi)是指xi项在树中的深度。因为树的递归特性再加二叉搜索树的应用广泛性使得用DP来求解这个最优化问题最合适不过。求解思路还是一样,目标是要列出DPFE,那么第一步要理解目标并把状态定义出来,有了状态和执行步骤,转移方程自然就OK了。因为面临的是建树的问题,所以我们的思路会自然想到,自底向上还是自顶向下?而不失一般性的一个规律是,如果是动态规划解,多数是自顶向下,而贪心解可以做自底向上。所以我们不妨以数据项集作为状态,即X为状态,那么自顶向下的执行步骤将是,首先从X中选择一个x作为节点,然后再计算去除x后的集合X’作为左右子树……依次递归。于是DPFE方程为:f(X)=min a{f(Xl) + f(Xr) + r(a,X)}, X≠∅,f(X)=0, X=∅。其中Xl={x属于X,且x<a}(左子树),Xr={x属于X,且x>a}。成本函数r(a,X)=Σp(x) x∈X。看到这个解,其实对于熟悉树结构的人来说,这是非常直观和自然的一个推断结果。
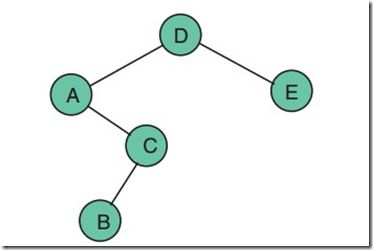
以具体例子来解读,一个数据集为{A,B,C,D,E},对应的搜索概率为{0.25,0.05,0.2,0.4,0.1}。那么最优解f(X)=f({A,B,C,D,E})=1.9,树形为:
程序源码:
1: /*
2: * Copyright (C) 2013 changedi
3: *
4: * Licensed under the Apache License, Version 2.0 (the "License");
5: * you may not use this file except in compliance with the License.
6: * You may obtain a copy of the License at
7: *
8: * http://www.apache.org/licenses/LICENSE-2.0
9: *
10: * Unless required by applicable law or agreed to in writing, software
11: * distributed under the License is distributed on an "AS IS" BASIS,
12: * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
13: * See the License for the specific language governing permissions and
14: * limitations under the License.
15: */
16: package com.jybat.dp;
17:
18: import java.util.SortedSet;
19: import java.util.TreeSet;
20:
21: public class BST {
22:
23: private int[] data = { 0, 1, 2, 3, 4 };// assume the n data items are
24: // the ints {0,1,..,n-1}
25: // corresponding to strings
26: // { "A", "B", "C", "D",
27: // "E"}
28: private double[] probability = { 0.25, 0.05, 0.2, 0.4, 0.1 };
29:
30: private static SortedSet<Integer> setOfAllItems = new TreeSet<Integer>();
31:
32: public BST() {
33: for (int i = 0; i < data.length; i++)
34: setOfAllItems.add(data[i]);
35: }
36:
37: private double sumOfProbabilitiesOfItems(SortedSet items) {
38: double result = 0.0;
39: for (int i = ((Integer) items.first()).intValue(); i <= ((Integer) items
40: .last()).intValue(); i++) {
41: result += probability[i];
42: }
43: return result;
44: }
45:
46: private SortedSet setOfItemsLessThanPivot(SortedSet items, int alpha) {
47: // conveniently use method headSet() from SortedSet
48: // headSet() DOES NOT include alpha
49: return new TreeSet(items.headSet(new Integer(alpha)));
50: }
51:
52: private SortedSet setOfItemsGreaterThanPivot(SortedSet items, int alpha) {
53: // conveniently use method tailSet() from SortedSet
54: // headSet() DOES include alpha
55: SortedSet ss = new TreeSet(items.tailSet(new Integer(alpha)));
56: ss.remove(alpha);
57: return ss;
58: }
59:
60: public double f(SortedSet<Integer> items) {
61: if (items.size() == 0)
62: return 0.0;
63: double min = Double.MAX_VALUE;
64: for (int a : items) {
65: double t = sumOfProbabilitiesOfItems(items)
66: + f(setOfItemsLessThanPivot(items, a))
67: + f(setOfItemsGreaterThanPivot(items, a));
68: if (t < min)
69: min = t;
70: }
71: return min;
72: }
73:
74: /**
75: * @param args
76: */
77: public static void main(String[] args) {
78: BST bst = new BST();
79: System.out.println(bst.f(setOfAllItems));
80: }
81:
82: }