深入理解动态规划的一系列问题（12）
今天介绍三个经典问题，为什么直接来三个？大概是因为这三个问题我觉得太经典了，以至于在任何人学习任何语言时都可能要实现这些题目的编程训练，所以这里就放到一起，打包讲下求解这些问题的动态规划思路（虽然有些问题不是那么直观的动态规划解）。
第一个问题是编辑距离（Edit Distance Problem)EDP问题，这个问题在维基上有全面的解释，并附有准确的代码实现（也叫levenshtein距离），我这里就简单讲下递归的DP解法。编辑距离需要一些前置条件，首先是距离的定义：对于两个字符串x和y，其中x包含m个字符，y包含n个字符，目标是由x串经过一系列允许的操作后变到y串，这些操作包括：1）删除操作D，删掉任意一个字符，成本为c(D)；2）插入操作I，插入任意一个字符，成本为c(I)；3）替换操作R，替换掉字符串中的一个字符，成本为c(R)。当然变为y串后要求变化成本最优。这就是一个典型的DP问题了。定义状态(i,j)为x串的前i个字符（即i串前缀），y串的j串前缀，于是DPFE为：
。换种表达就是
，转移函数t表示如下：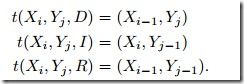
。目标就是计算f(x,y)。
举例来说：x="CAN”，y=”ANN”，三种操作的成本均为1，求x和y的编辑距离。（答案为2，具体求解见下面代码）
源码求解：
1: /*
2: * Copyright (C) 2013 changedi
3: *
4: * Licensed under the Apache License, Version 2.0 (the "License");
5: * you may not use this file except in compliance with the License.
6: * You may obtain a copy of the License at
7: *
8: * http://www.apache.org/licenses/LICENSE-2.0
9: *
10: * Unless required by applicable law or agreed to in writing, software
11: * distributed under the License is distributed on an "AS IS" BASIS,
12: * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
13: * See the License for the specific language governing permissions and
14: * limitations under the License.
15: */
16: package com.jybat.dp;
17:
18: //EditDistanceProblem;
19: public class EDP {
20:
21: private static String s1 = "CAN";
22: private static String s2 = "ANN";
23: private static final int insertionCost = 1;
24: private static final int deletionCost = 1;
25: private static final int replacementCost = 1;
26: // it is useful to have the string lengths as symbolic constants
27: private static int s1Length = s1.length();
28: private static int s2Length = s2.length();
29:
30: // The decision space is constant in this example.
31: // It does not depend on the current state.
32: // We chose to code the 3 allowed operations
33: // as follows:
34: // 1 stands for delete
35: // 2 stands for insert
36: // 12 stands for replace
37: private static int[] decisionSet = { 1, 2, 12 };
38:
39: // costOfOperation()
40: // returns 0 if the specified characters in the 2 strings
41: // match and the decision is to perform
42: // "replacement" operation for matching chars
43: // (whose cost is usually defined as 0)
44: // returns 1 otherwise (if delete, insert, or a real replacement operation
45: // happens)
46: private static int costOfOperation(int i, int j, int dec) {
47: if (dec == 12) { // dec==12 means decision is to replace
48: if (s1.charAt(i - 1) // note: subtract 1 because array
49: // starts at index 0
50: == s2.charAt(j - 1)) { // matching chars, cost is 0
51: return 0;
52: } else { // real replacement
53: return replacementCost; // cost of real replacement
54: }
55: }
56: if (dec == 1) { // dec==1 means decision is to delete
57: return deletionCost;
58: }
59: // otherwise it must be that dec==2, decision to insert
60: return insertionCost;
61: }
62:
63: private static int s1Adjustment(int dec) {
64: if (dec == 2) { // insert
65: return 0;
66: }
67: return 1;
68: }
69:
70: private static int s2Adjustment(int dec) {
71: if (dec == 1) { // delete
72: return 0;
73: }
74: return 1;
75: }
76:
77: public static int d(int i, int j) {
78: if (i == 0)
79: return j;
80: if (j == 0)
81: return i;
82: int min = Integer.MAX_VALUE;
83: for (int dec : decisionSet) {
84: int t = costOfOperation(i, j, dec)
85: + d(i - s1Adjustment(dec), j - s2Adjustment(dec));
86: if (t < min)
87: min = t;
88: }
89: return min;
90: }
91:
92: /**
93: * @param args
94: */
95: public static void main(String[] args) {
96: System.out.println(d(s1Length, s2Length));
97:
98: }
99:
100: }
第二个问题是大家非常熟悉的斐波那契数列问题Fibonacci Recurrence Relation (FIB)：
斐波那契数列就是一个经典的f(n)=f(n-1)+f(n-2)的递归问题。这里不讲，只是列出这个问题。
第三个问题是汉诺塔问题Tower of Hanoi Problem (HANOI)：
汉诺塔的问题描述就省去了，主要是定义状态，我们定义在移动了i个碟子后的最优步数为f(i)，则f(i)=2f(i-1)+1，即通用的汉诺塔策略：将碟子先移动到中间柱，移动i-1个后，将第i个碟子移动到目标柱，然后再重复将i-1个柱子以同样的方法放回目标柱，于是这个dp方程就可以理解了。但是这样子的方程看上去总不像动态规划那明细的阶段和状态的对应，于是我们修正一下方程如下：f(m,i,j,k)=opt {f(m-1,i,k,j)+f(1,i,j,k)+f(m-1,k,j,i)}。状态(m,i,j,k)表示把m个碟子从i移动到j的最优步数，k代表中间那个柱。
DP源码如下：
1: /*
2: * Copyright (C) 2013 changedi
3: *
4: * Licensed under the Apache License, Version 2.0 (the "License");
5: * you may not use this file except in compliance with the License.
6: * You may obtain a copy of the License at
7: *
8: * http://www.apache.org/licenses/LICENSE-2.0
9: *
10: * Unless required by applicable law or agreed to in writing, software
11: * distributed under the License is distributed on an "AS IS" BASIS,
12: * WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
13: * See the License for the specific language governing permissions and
14: * limitations under the License.
15: */
16: package com.jybat.dp;
17:
18: //tower of hanoi problem
19: //Compute the number of moves when the recursive
20: //strategy is used.
21: public class HANOI {
22:
23: // m: number of disks to move
24: // i: index of source tower
25: // j: index of destination tower
26: // k: index of temporary tower
27: public static int f(int m, int i, int j, int k) {
28: if (m == 1)
29: return 1;
30: return f(m - 1, i, k, j) + f(1, i, j, k) + f(m - 1, k, j, i);
31: }
32:
33: /**
34: * @param args
35: */
36: public static void main(String[] args) {
37: System.out.println(f(3,1,2,3));
38: }
39:
40: }
总结下，其实这三个问题，除了编辑距离外，fib和hanoi都更像是递归教学而不是DP，但是其实从问题的结构上讲，hanoi这样的是典型的动态规划求解，只不过过多的教科书和经验把它们放到了递归里，同时又忽略了递归和DP的联系。所以我这里把它们放到一起，用来说明动态规划问题也包含经典的递归问题的。