数据结构与算法分析:哈希表
以下是阅读了《算法导论》后,对哈希表的一些总结:
哈希表又叫散列表,是实现字典操作的一种有效数据结构。哈希表的查询效率极高,在没有冲突(后面会介绍)的情况下可做到一次存取便能得到所查记录,在理想情况下,查找一个元素的平均时间为O(1)(最差情况下散列表中查找一个元素的时间与链表中查找的时间相同:O(n),但实际情况中一般散列表的性能是比较好的)。
哈希表就是描述key—value对的映射问题的数据结构,更详细的描述是:在记录的存储位置和它的关键字之间建立一个确定的对应关系h,使每个关键字与哈希表中唯一一个存储位置相对应。我们称这个对应关系f为哈希/散列函数,这个存储结构即为哈希/散列表。
一、直接寻址表
当关键字的全域U比较小时,直接寻址是一种简单而有效的技术,它的哈希函数很简单:f(key) = key,即关键字大小直接与元素所在的表位置序号相等。如果关键字不是整数,我们需要通过某种手段将其转换为整数,比如可以将字符关键字转化为其在字母表中的序号作为关键字。直接寻址法的优点是不会出现两个关键字对应到同一个地址的情况(即不会出现f(key1) = f(key2)的情况),因此不用处理冲突。但是,直接寻址表也有着天然的局限性,即如果全域U很大,则在一台标准的计算机可用内存容量中,要存储大小为U的一张表并不实际。
二、散列表
上面说到,在处理实际数据的时候,全域U往往会很大,则在一台标准的计算机可用内存容量中,要存储大小为U的一张表也许不太实际,此时实际需要存储的关键字集合K可能相对U来说很小,这时散列表需要的存储空间要比直接表少很多。
散列表T通过散列函数f计算出关键字key在表中的位置,这些位置被称为“槽”。散列函数f将关键字域U映射到散列表T[0...m-1]的槽位上。由于关键字的个数要大于槽的个数,这里会出现一个问题:若干个关键字可能映射到了表的同一个位置处,我们称这种情形为冲突。我们希望散列表在节省空间的同时,其性能要接近于O(1),因此需要尽量避免冲突,通常的策略是尽可能地设计更好的哈希函数f,将关键字尽可能随机地映射到散列表的每个位置上(为什么说尽可能?因为这里关键字的个数|U|肯定大于散列表的槽个数m,因此至少有两个关键字被映射到同一个槽中,只依靠哈希函数f是无法完全避免冲突的)。
三、哈希函数
哈希函数的构造方法很多,最好的情况是:对于关键字结合中的任一个关键字,经哈希函数映射到地址集合中任何一个地址的概率相等,也就是说,关键字经过哈希函数得到一个随机的地址,以便使一组关键字的哈希地址均匀分布在整个地址空间中,从而减少冲突。同样,由于多数哈希函数都是假定关键字的全域为自然数集N={0、1、2….},因此所给关键字如果不是自然数,就要先想办法将其转换为自然数。下面我们就来看常用的哈希函数。
1.直接定址法
对应前面的直接寻址表,关键字与哈希表中的地址有着一一对应关系,因此不需要处理冲突。
2.除法散列法
哈希函数:f(key) = key % m
函数对所给关键字key取余,这里 m 必须不能大于哈希表的长度len,通常 m 可取一个不太接近2的整数次幂的素数。
3.乘法散列法
用关键字key乘上A(0 < A < 1),取出其小数部分,然后用 m 乘以小数的值,再向下取整,该函数写为:f(key) = floor(m * (key * A % 1))
其中,(key * A % 1)是取(key * A)的小数部分,该函数涉及到参数A的取值问题。Knuth认为,A = (sqrt(5)-1)/2 = 0.6180339877...是个比较理想的值,事实上,该点就是黄金分割点。
除法散列法和乘法散列法是较为常用的哈希函数设计方法,事实上方法还有很多种,如全域散列法、折叠法、数字分析法等,更多的介绍请参考相关书籍。
四、冲突处理
前面提到,为了节省空间,表中槽的数目小于关键字的数目,只是通过设计好的哈希函数不可能完全避免冲突。下面介绍两种解决冲突的方法:链接法和开放定址法。
1.链接法(chaining)
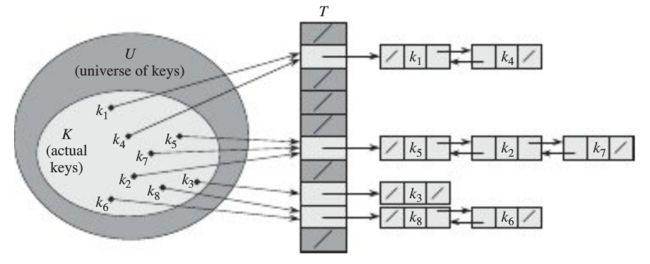
链接法的思路很简单:如果多个关键字映射到了哈希表的同一个位置处(将这些关键字称为同义词),则将这些同义词记录在同一个线性链表中,该槽有一个指针,它指向存储所有散列到该槽的元素的链表表头,如下图所示:
图中,关键字k1和k4映射到了哈希表的同一个位置处,k5、k2、k7映射到了哈希表的同一个位置处。《算法导论》提到,为了更快地删除某个元素,可以将链表设计为双向链表。如果表是单链接的,则为了删除元素x,首先必须在表T[h(x,key)]中找到元素x,然后通过更改x的前去元素的next属性,把x从链表中删除。在单链表的情况下,删除和查找操作的渐近运行时间相同。另一个例子如下:
2.开放定址法(open addressing)
在开放定址法中,所有的元素都存放在散列表中,也即是说,每个表项或包含动态集合的一个元素,或为空,不再使用链表。哈希表中的槽t不仅向哈希函数值等于t的同义词开放,而且向哈希函数值不等于t的记录开放,允许以“抢占”的方式争取哈希地址。
该方法采用如下公式记性再散列:
F(key,i) = (f(key) + di) % len
其中,f(key)为哈希函数,len为哈希表长,di为增量序列,它可能有如下三种情况:
di = 1,2,3...m-1di = 1,-1,4,-4,9,-9...k^2,-k^2di为伪随机序列
采用第一种序列的叫做线性探测再散列,采用第二种序列的叫做二次探测再散列,采用第三种序列的叫做随机探测再散列。说白了,就是在发生冲突时,将关键字应该放入的位置向前或向后移动若干位置,比如采取第一种序列时,如果遇到冲突,就向后移动一个位置来检测,如果还发生冲突,继续向后移动,直到遇到一个空槽,则将该关键字插入到该位置处。
线性探测比较容易实现,但是它存在一个问题,称为一次群集。随着连续被占用的槽不断增加,平均查找时间也随之不断增加,群集现象很容易出现,这是因为当一个空槽前有i个满槽时,该空槽为下一个将被占用的概率为(di+1)len。
同样采用二次探测的方法,会产生二次群集,因为每次遇到冲突时,寻找插入位置时都是在跳跃性前进或后退,因此这个相对于一次群集来说,比较轻度。
五、一些例子
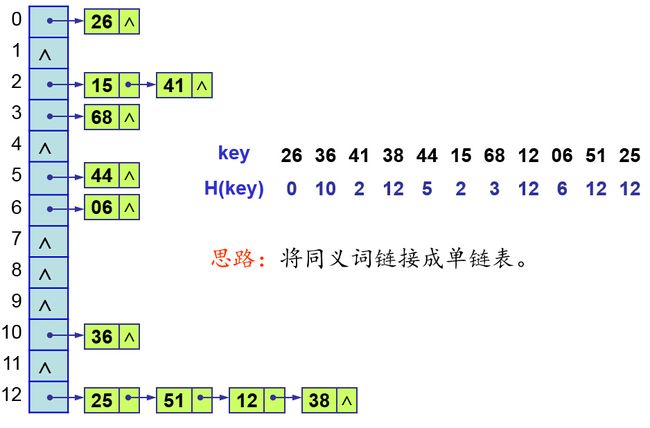
已知关键字序列:26,36,41,38,44,15,68,12,06,51,25。
用除法散列法构造哈希函数,线性探测再散列法解决冲突。现在需要:①建哈希表;②求查找成功和失败的平均搜索长度(ASL)。
解法:题中关键字个数n = 11,设装载因子α = 0.75,m = n / α,取m为素数13。哈希函数:f(key) = key % 13,以下图片给出了建哈希表的步骤:
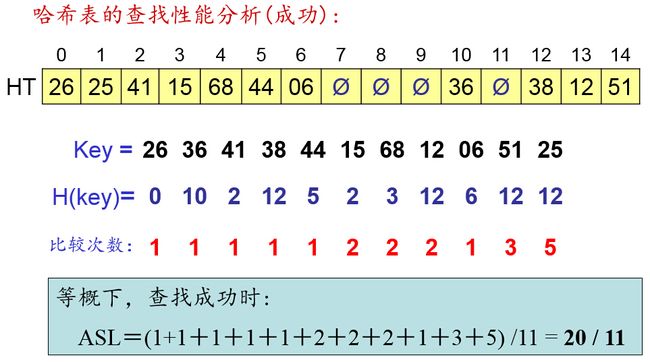
哈希表的查找性能分析:
六、代码实现
下面用代码实现一个哈希表,这里采用链接法来处理冲突,描述数据结构的头文件的代码如下:
#define M 7 //哈希函数中的除数,必须小于等于表长
typedef int ElemType;
// 该哈希表采用链接法解决冲突问题
typedef struct Node
{ //Node为链表节点的数据结构
ElemType data;
struct Node *next;
}Node,*pNode;
// 哈希表每个槽的数据结构
typedef struct HashNode
{
pNode first; // first指向链表的第一个节点
}HashNode,*HashTable;
// 创建哈希表
HashTable create_HashTable(int);
// 在哈希表中查找数据
pNode search_HashTable(HashTable, ElemType);
// 插入数据到哈希表
bool insert_HashTable(HashTable,ElemType);
// 从哈希表中删除数据
bool delete_HashTable(HashTable,ElemType);
// 销毁哈希表
void destroy_HashTable(HashTable,int);首先建立一个空哈希表,而然后执行插入、删除、查询等操作,最后销毁哈希表,哈希表的实现代码如下:
#include<stdio.h>
#include<stdlib.h>
#include "data_structure.h"
// 创建n个槽的哈希表
HashTable create_HashTable(int n)
{
int i;
HashTable hashtable = (HashTable)malloc(n*sizeof(HashNode));
if(!hashtable)
{
printf("hashtable malloc faild,program exit...");
exit(-1);
}
// 将哈希表置空
for(i=0;i<n;i++)
hashtable[i].first = NULL;
return hashtable;
}
// 在哈希表中查找数据,哈希函数为H(key)=key % M
// 查找成功则返回在链表中的位置
// 查找不成功则返回NULL
pNode search_HashTable(HashTable hashtable, ElemType data)
{
if(!hashtable)
return NULL;
pNode pCur = hashtable[data%M].first;
while(pCur && pCur->data != data)
pCur = pCur->next;
return pCur;
}
// 向哈希表中插入数据,哈希函数为H(key)=key%M
// 如果data已存在,则返回fasle
// 否则,插入对应链表的最后并返回true
bool insert_HashTable(HashTable hashtable,ElemType data)
{
// 如果已经存在,返回false
if(search_HashTable(hashtable,data))
return false;
// 否则为插入数据分配空间
pNode pNew = (pNode)malloc(sizeof(Node));
if(!pNew)
{
printf("pNew malloc faild,program exit...");
exit(-1);
}
pNew->data = data;
pNew->next = NULL;
// 将节点插入到对应链表的最后
pNode pCur = hashtable[data%M].first;
if(!pCur) // 插入位置为链表第一个节点的情况
hashtable[data%M].first = pNew;
else // 插入位置不是链表第一个节点的情况
{ // 只有用pCur->next才可以将pNew节点连到链表上,
// 用pCur连不到链表上,而是连到了pCur上
// pCur虽然最终指向链表中的某个节点,但是它并不在链表中
while(pCur->next)
pCur = pCur->next;
pCur->next = pNew;
}
return true;
}
// 从哈希表中删除数据,哈希函数为H(key)=key % M
// 如果data不存在,则返回fasle,
// 否则,删除并返回true
bool delete_HashTable(HashTable hashtable,ElemType data)
{
// 如果没查找到,返回false
if(!search_HashTable(hashtable,data))
return false;
// 否则,删除数据
pNode pCur = hashtable[data%M].first;
pNode pPre = pCur; // 被删节点的前一个节点,初始值与pCur相同
if(pCur->data == data) // 被删节点是链表的第一个节点的情况
hashtable[data%M].first = pCur->next;
else
{ // 被删节点不是第一个节点的情况
while(pCur && pCur->data != data)
{
pPre = pCur;
pCur = pCur->next;
}
pPre->next = pCur->next;
}
free(pCur);
pCur = 0;
return true;
}
// 销毁槽数为n的哈希表
void destroy_HashTable(HashTable hashtable,int n)
{
int i;
// 先逐个链表释放
for(i=0;i<n;i++)
{
pNode pCur = hashtable[i].first;
pNode pDel = NULL;
while(pCur)
{
pDel = pCur;
pCur = pCur->next;
free(pDel);
pDel = 0;
}
}
// 最后释放哈希表
free(hashtable);
hashtable = 0;
}最后测试代码:
#include<stdio.h>
#include "data_structure.h"
int main()
{
int len = 15; // 哈希表长,亦即表中槽的数目
printf("We set the length of hashtable %d\n",len);
//创建哈希表并插入数据
HashTable hashtable = create_HashTable(len);
if(insert_HashTable(hashtable,1))
printf("insert 1 success\n");
else
printf("insert 1 fail,it is already existed in the hashtable\n");
if(insert_HashTable(hashtable,8))
printf("insert 8 success\n");
else
printf("insert 8 fail,it is already existed in the hashtable\n");
if(insert_HashTable(hashtable,3))
printf("insert 3 success\n");
else
printf("insert 3 fail,it is already existed in the hashtable\n");
if(insert_HashTable(hashtable,10))
printf("insert 10 success\n");
else
printf("insert 10 fail,it is already existed in the hashtable\n");
if(insert_HashTable(hashtable,8))
printf("insert 8 success\n");
else
printf("insert 8 fail,it is already existed in the hashtable\n");
//查找数据
pNode pFind1 = search_HashTable(hashtable,10);
if(pFind1)
printf("find %d in the hashtable\n",pFind1->data);
else
printf("not find 10 in the hashtable\n");
pNode pFind2 = search_HashTable(hashtable,4);
if(pFind2)
printf("find %d in the hashtable\n",pFind2->data);
else
printf("not find 4 in the hashtable\n");
//删除数据
if(delete_HashTable(hashtable,1))
printf("delete 1 success\n");
else
printf("delete 1 fail");
pNode pFind3 = search_HashTable(hashtable,1);
if(pFind3)
printf("find %d in the hashtable\n",pFind3->data);
else
printf("not find 1 in the hashtable,it has been deleted\n");
// 销毁哈希表
destroy_HashTable(hashtable,len);
return 0;
}
七、参考资料
《算法导论》 第三版 (美)科曼(Cormen,T.H.) 等著,殷建平 等译
http://blog.csdn.net/ns_code