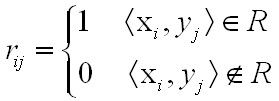二元关系的矩阵和图表示

两个事物之间的关系称之为二元关系。在数学上，二元关系指的是这样的一个集合S，它的所有元素都为二元有序对。它反映的是有序对中第一个元素组成的集合与第二个元素组成的集合之间的关系。举个例子，集合S={<天秤座,libra>,<狮子座,leo>} 就表示了中文集合{天秤座,狮子座}与英文集合{libra,leo}之间的对应关系。

二元关系可以用集合表示，就像我们上面提到的。而除此之外，还可以用其他数学工具来描述它——矩阵和图。矩阵的基本元素是数字及其所处的位置。直觉上，我们很自然的想到用它的下标来体现两个集合中的元素，用数字体现它们是否具有关系。这便得出了以下定义：

【定义】设集合A={x₁,x₂,…,x_m},B={y₁,y₂,…,y_n}，R为A,B之间的二元关系。称矩阵M(R)=(r_ij)_m×n为R的关系矩阵，其中

这样我们定义了一个映射，把集合R映射为一个矩阵M。如此定义，首先保证了R的集合表达式和R的关系矩阵是一一对应的。其次，这样的定义会带来很多好的性质。我们可以应用矩阵的语言把整个二元关系的理论重新叙述一遍：

• 关系R的逆，记作R^-1，表示的是集合{<x,y>|<y,x>εR}，我们有 M(R^-1)=(M(R))^T. 这样，我们求关系的逆就转化为了求一个矩阵的转置矩阵。
  

• 两个关系的合成(复合)，记作R₂•R₁,表示的是集合

为了用矩阵表示关系的合成，我们可以定义{0,1}中元素的加法为逻辑加法(0+0=0,0+1=1,1+0=1,1+1=1)，于是便有

M(R₂•R₁)=M(R₁)•M(R₂)

这样，关系的合成这一运算就转化为了矩阵的相乘。

• R在D上的限制就等价于找M(R)中相应行中为1的元素；D在R下的象就等价于M(R)中相应行为1的元素的列坐标。
• 关系R是单根的，指的是对任意的yεranB,存在唯一的xεdomR，使得<x,y>εR。这意味着M(R)的每一列有且仅有一个1
• 关系R是单值的，指的是对任意的xεdomR,存在唯一的yεranB，使得<x,y>εR。这意味着M(R)的每一行有且仅有一个1
  

特殊的，集合A上的二元关系R指的是A×A={<x,y>|xεA,yεA}。这样像前面第二条性质就有M(R²)=(M(R))²

• 自反的二元关系R相应的关系矩阵主对角线元素都为1
• 反自反的二元关系R相应的关系矩阵主对角线元素都为0
• 对称的二元关系R相应的关系矩阵也是对称的
• 反对称的二元关系R相应的关系矩阵也是反对称的(这里定义1的反为0)
• 对传递的二元关系R，相应的关系矩阵R中若r_ij=1,r_jk=1，则r_ik=1
  

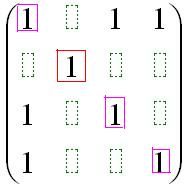
等价关系R(同时具有自反，对称，传递性质的二元关系)可以确定集合A上的一个划分，那么如何从关系矩阵中找出相应的等价类？如下图所示:

如何用图来表示等价关系呢？由于关系中的元素是有序对，直觉上，我们很自然的想到用有向图。于是定义如下：

【定义】设集合A={x₁,x₂,…,x_m},B={y₁,y₂,…,y_n}，R为A,B之间的二元关系。以A,B中的元素为顶点，若<x_i,y_j>εR，则从顶点x_i向y_j引有向边，称所画出的图G(R)为R的关系图。
这样，我们就可以用图论的语言把整个二元关系的理论重新叙述一遍：

• R的逆：只需把图中的箭头反向
• 两个关系的合成：通过过渡集合把两个图拼接为一个图，然后把长为2的有向通路变为起点指向终点的长为1的有向通路
• R在D上的限制就等价于找G(R)中起点包含在集合D中的部分；D在R下的象就等价于G(R)中包含在集合D中的起点所指向的终点
• 关系R是单根的，指B中顶点的入度均为1
• 关系R是单值的，指A中顶点的出度均为1

特殊的，集合A上的二元关系R对应的关系图将为多重图(有重边和环的出现)。

• 自反的二元关系R相应的关系图每个顶点处都有环
• 反自反的二元关系R相应的关系图每个顶点处都无环
• 对称的二元关系R相应的关系图中两个顶点间如果存在有向边，必有两条反向的有向边
• 反对称的二元关系R相应的关系图中两个顶点间的有向边必是单重的
• 对传递的二元关系R，相应的关系图中长度为2的有向通路的起点和终点间必存在由起点指向终点的有向线段

如何从关系图中找出一个等价关系所确定的划分？
对于二元关系中的其他一些理论(如闭包和序关系)，用关系矩阵和关系图描述一下试试。我们经常把一件事物抽象为数学模型来表达。有时换一种数学工具可能在处理某些运算时给我们带来方便。用不同的工具思考，能更深刻的理解数学各个分支之间的联系。

关于Discrete Mathematics更多讨论与交流，敬请关注本博客和新浪微博songzi_tea.