《数据结构与算法分析》哈希表(散列)简介与实现
前言:
这两天等阿里的电话等了好久了,一直没有消息,是不是已经把我刷了。。不过不管这么多,该学习还是要学习的,简历都没过关证明我还需要更加的努力。这两天回家了,休息一下,然后进入下一个阶段的奋斗吧。
我的github:
我实现的代码全部贴在我的github中,欢迎大家去参观。
https://github.com/YinWenAtBIT
介绍:
定义:
哈希表(Hash Table)也叫散列表,是根据关键码值(Key Value)而直接进行访问的数据结构。它通过把关键码值映射到哈希表中的一个位置来访问记录,以加快查找的速度。这个映射函数就做散列函数,存放记录的数组叫做散列表。
散列存储的基本思路
以数据中每个元素的关键字K为自变量,通过散列函数H(k)计算出函数值,以该函数值作为一块连续存储空间的的单元地址,将该元素存储到函数值对应的单元中。
哈希表查找的时间复杂度
哈希表存储的是键值对,其查找的时间复杂度与元素数量多少无关,哈希表在查找元素时是通过计算哈希码值来定位元素的位置从而直接访问元素的,因此,哈希表查找的时间复杂度为O(1)。
哈希函数:
使用哈希表的第一步就是如何根据键值来求取对应的Index,一般使用的方式有如下几种,原理也非常简单,大家可以自行实现,不过选取哪一个,通常还是需要根据键值的特点来决定。
1. 直接寻址法:取关键字或关键字的某个线性函数值为散列地址。即H(key)=key或H(key) = a•key + b,其中a和b为常数(这种散列函数叫做自身函数)
2. 数字分析法
3. 平方取中法
4. 折叠法
5. 随机数法
6. 除留余数法:取关键字被某个不大于散列表表长m的数p除后所得的余数为散列地址。即 H(key) = key MOD p, p<=m。不仅可以对关键字直接取模,也可在折叠、平方取中等运算之后取模。对p的选择很重要,一般取素数或m,若p选的不好,容易产生同义词。
处理
解决冲突:
在进行求取键值的过程中,必然会遇上不同的键值映射到同一个Index的情况,那么这个时候如何解决这个冲突呢。 主要的方法有三种:
1. 分离链接法:这种方法是把有相同散列值的Key都用一个表保存下来,可以使用链表来实现。
2.开放定址法:这种方法是在遇到了冲突之后,选择尝试哈希表中另外的部分,这就需要重新计算键值。
3.再散列:当遇到哈希表中一半都被填满的时候,这时候插入和查找的效率必然就会降低将许多,这时创建一个新的哈希表,比原来的大一倍,然后使用一个相关的新的哈希函数,把原有的元素重新插入表中。
编码实现:
分离链接法:
在这里我使用了不同与书上的方法,书上使用的是带有头结点的方式,我编码使用的是不带头结点的方式。在编码时使用了我自谦编写的带有头结点的链表源代码,并且修改成了不带头结点的链表。
.h文件,使用的哈希方式是平方取中法。
#include "list.h"
#ifndef _HASH_TABLE
#define _HASH_TABLE
struct HashTbl;
typedef HashTbl * HashTable;
typedef int ElementType;
HashTable initializeTable(int TableSize);
void DestroyTable(HashTable H);
Position FindKey(ElementType Key, HashTable H);
void insertKey(ElementType Key, HashTable H);
void deleteKey(ElementType Key, HashTable H);
void PrintHashTable(HashTable H);
/*平方取中法*/
int Hash(ElementType Key, int TableSize);
struct HashTbl
{
int TableSize;
List * TheList;
};
#endif
哈希函数:
int Hash(ElementType Key, int TableSize)
{
int temp;
temp = Key*Key/100%100;
return temp%TableSize;
}
哈希表初始化:
/*无头结点,使用calloc给所有指针赋值为0*/
HashTable initializeTable(int TableSize)
{
HashTable H;
H = (HashTable)malloc(sizeof(struct HashTbl));
if( H == NULL)
{
fprintf(stderr,"not enough memory");
exit(1);
}
H->TableSize = NextPrime(TableSize);
H->TheList = (List *)calloc(H->TableSize, sizeof(List));
if(H->TheList == NULL)
{
fprintf(stderr,"not enough memory");
exit(1);
}
return H;
}
插入键值:
void insertKey(ElementType Key, HashTable H)
{
Position P;
List L;
L = H->TheList[Hash(Key, H->TableSize)];
/*没有节点*/
if(L == NULL)
{
P = (Position)malloc(sizeof(Node));
P->Element = Key;
P->Next = NULL;
H->TheList[Hash(Key, H->TableSize)] = P;
}
else
{
P = find(Key, L);
if(P == NULL)
{
P = (Position)malloc(sizeof(Node));
P->Element = Key;
P->Next = L;
H->TheList[Hash(Key, H->TableSize)] = P;
}
}
}
删除键值:
void deleteKey(ElementType Key, HashTable H)
{
List L;
Position P;
L = H->TheList[Hash(Key, H->TableSize)];
P = find(Key, L);
if(P == NULL)
fprintf(stderr, "%d do not exist\n", Key);
else
{
/*被删除的元素为第一个*/
if(L == P)
{
H->TheList[Hash(Key, H->TableSize)] = P->Next;
free(P);
}
else
{
Position front;
front = findPrevious(Key, L);
front->Next = P->Next;
free(P);
}
}
}
查找键值:
Position FindKey(ElementType Key, HashTable H)
{
Position P;
List L;
L = H->TheList[Hash(Key, H->TableSize)];
P = find(Key, L);
if(P == NULL)
fprintf(stderr, "%d do not exist", Key);
return P;
}
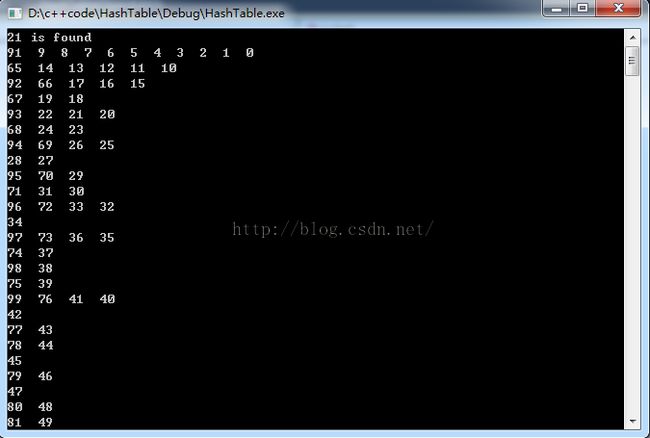
测试截图:
这里每一行代表一个链表。
在分离链接法中,如果没有头结点,就特别需要注意每个指针插入第一个元素的处理,稍微不注意就赋值失败了。开放定址法:
在这里我使用的是平方探测法。并且稍微对书本上的源代码进行了修改。节点定义如下:
/*令Empty默认为0,则使用calloc可以自动初始化为Empty*/
enum KindOfEntry
{
Empty =0,
Legitimate,
Deleted
};
struct HashEntry
{
ElementType Element;
enum KindOfEntry Info;
};
typedef struct HashEntry Cell;
struct HashTbl
{
int TableSize;
Cell * TheCells;
};
初始化哈希表:
/*无头结点,使用calloc给所有指针赋值为0*/
HashTable initializeTable(int TableSize)
{
HashTable H;
H = (HashTable)malloc(sizeof(struct HashTbl));
if( H == NULL)
{
fprintf(stderr,"not enough memory");
exit(1);
}
H->TableSize = NextPrime(TableSize);
H->TheCells = (Cell *)calloc(H->TableSize, sizeof(Cell));
if(H->TheCells == NULL)
{
fprintf(stderr,"not enough memory");
exit(1);
}
return H;
}
查找键值:
查找键值返回找到的点,或者第一个空的点,这样插入键值和删除键值就可以直接调用。
Position FindKey(ElementType Key, HashTable H)
{
Position P;
int collision =0;
P = Hash(Key, H->TableSize);
while(H->TheCells[P].Info != Empty && H->TheCells[P].Element != Key)
{
/* F(i) = F(i-1) +2i-1 */
P += 2* ++collision -1;
if(P > H->TableSize)
P -= H->TableSize;
}
return P;
}
插入键值:
查找要插入的键值,如果返回的点已经使用,那么代表元素已经存在,如果为空,则执行插入。
void insertKey(ElementType Key, HashTable H)
{
Position P;
P = FindKey(Key, H);
if(H->TheCells[P].Info !=Legitimate)
{
H->TheCells[P].Element = Key;
H->TheCells[P].Info = Legitimate;
}
}
删除键值:
同样先调用查找,如果有则删除。
void deleteKey(ElementType Key, HashTable H)
{
Position P;
P = FindKey(Key, H);
if(H->TheCells[P].Info ==Legitimate)
{
H->TheCells[P].Info = Deleted;
}
}
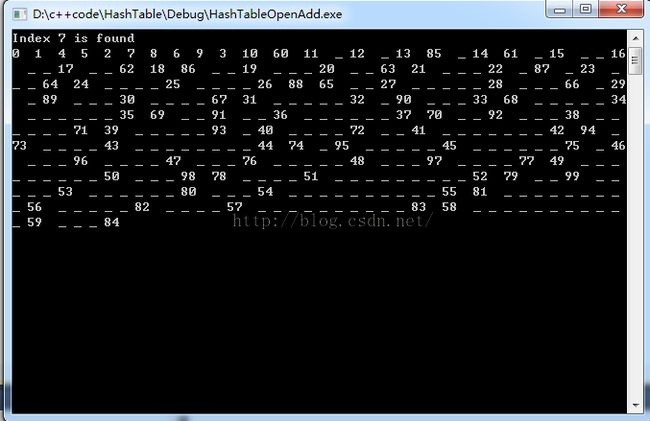
测试截图:
测试的时候用_表示未使用的节点。
在实现哈希表的时候遇上的困难不多,这个数据结构相对于树来说其实应该算简单不少的。唯一的问题就是我在使用自己写的list结构时,忘了原来的实现是带有头结点的,结果半天找不到错误。最后一步步调试才发现原来是这里出了问题。所以说,使用C++的东西的时候,最好还是知道里面是怎么实现的,不然容易进坑。