Sicily 1346 金明的预算方案 （SOJ 1346） 【DP 动态规划-背包问题】

原题地址：点击打开链接

这两天我消失就是为了做这题……用自己的方法做总是TLE，肯定是我对DP问题还不够熟练&理解深入，一怒之下看了两篇参考文档，一份是《国家集训队2009论文集浅谈几类背包题》，感觉写得很鸡肋，看得十分辛苦，可能因为我智商不够；但是看上面那篇还是有用的，因为里面引用了《背包问题九讲》，俗称的“背包九讲”，好东西来，网上处处能下载得到，比前一份易懂多了。

做了这题，鄙人感觉自己的DP水平提升了一个LEVEL，比原来要好一点。也搜了一下，发现我的代码还是比较短的，50行之内，不过运行时间达到0.7s，感觉很险……用的全部是纯数组，之前是过用vector等TLE。

hmmmm………………这题的题解应该怎么写……呢。强烈建议各位先看一下上面提到的《背包问题九讲》，说不定各位看完了就自己跑去做题然后做出来，也不用看我这篇日志了。

——————正文——————

《背包问题九讲》“官方”下载地址：点击打开链接

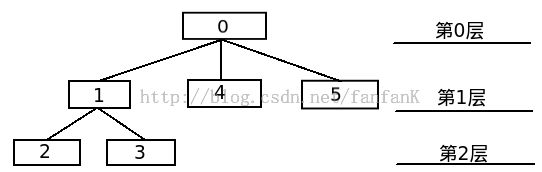
这题属于有依赖的背包问题，对于题目的样例，我先画个图：

现在我们就对题目进行抽象，每个节点都有这么几个属性：v,p,q,w，其中v是节点的花费，p是节点的重要性，这样我们令w=v*p作为节点的权值，还有q就是父节点的标号。

根据题意，我们要解决的就是给定一“棵”森林（森林即每个个节点可以有超过2个子节点的树），分配给0号节点n元（花费），问森林总的权值最大是多少——这里需要注意的是，必须要一个节点被分配了超过其花费v的钱数，才可以被“激活”。

使用背包的解体思路，我们可以想到01背包的解决方法，就是对于第1层的节点，你可以选择“激活”或“不激活”两种情况，然而，和01背包又十分不同的是，分配给某一个节点的花费不是唯一的，就像1号节点，你分配给它的金钱越多，那么以1号节点为根的森林的总权值可能就越大。面对这样的情况，因此01背包就不适用了。但是像处理完全背包一样，对于每个节点（实际是第1层的节点），我们可以给它们都分配vi~n的钱，然后看更新所得的结果，这样的话，对于第1层来说，状态转移方程如下：

F[i,j] = max( F[i-1,j] , F[i-1 , j-V] + W)；

 //F[i,j]表示选择第i件物品后（前面的i-1件物品也已经完成挑选），使用了j元所获得的最大权值是多少。其中V表示以i为根节点的森林总的花费（即分配给i节点的金钱），W表示以i为根节点的森林从的权值（当然权值仅仅由被“激活”的节点来提供）

当然，其实这个方程还可以变得更简单一些，就是在迭代的过程中，直接使用下面这条就可以了：

F[j] = max( F[j] , F[j-V] + W)；

这样就减少了空间复杂度，為什麼可以这么做呢，因为每次对于F[i, ...]来说，它的状态肯定是由F[i-1, ... ]得到的，这样我们就直接把第一维省去，只要我们在计算的时候，令j为从n~V就可以了，这样每次更新F[j]（等式左边），在等式右边的F[...] 都是上一次迭代的结果（相当于F[i-1, ...]）。

好了，现在的关键问题就是V和W要怎么搞？

很显然，对于节点i（再次强调啊刚才的操作都是针对第1层节点的），V肯定要大于等于vi，因为这样节点i才能够被激活。那多出来的部分：V-vi——怎么办？很简单，分配给节点i的子节点，看看子节点能够凑出的最大权值之和是多少。也就是说，对于第2层的节点，它们可以使用的金钱是V-vi，那就完全变成了01背包问题——给n元，对于每个节点，“激活”或者“不激活”，因此W就可以计算出来了，其等于节点i的权值加上子节点的权值之和。

这里有个地方需要注意，就是我们并不需碰到每个V，都对第二层节点进行一次01背包，我们一开始就对第二层的节点进行01背包，假设直接分配给这些节点的钱是n-vi，因为父节点的花费是vi，而从的钱数是n，因此子节点们最多能使用n-vi元。状态转移方程是：

f[i,j,k]=max(f[i,j-1,k],f[i,j-1,k-vj]+wj);

//其中f[i,j,k]表示选择以节点i为父节点的第j个子节点后，花费为k时的能获得的最大权值

同上面一样，这个方程可以简化为如下形式：

f[i,k]=max(f[i,k],f[i,k-vj]+wj);

这样我们就知道了在给节点i的子节点们分配0~n-vi元时，最大的权值之和分别是多少了。

好了，那么原本的上面的方程就写成了：

F[j] = max( F[j] , F[j-V] + wi + f[i,V-vi])；

还有一个特别提醒：题目中说所有的物品价钱都是10的倍数，复杂度降低了

下面就直接写代码了，代码如下：

#include<iostream>
#include<stdio.h>
#include<memory.h>
#include<algorithm>
#define MAXM 65
#define MAXN 32055
using namespace std;
int n,m;
int v[MAXM],p[MAXM],q[MAXM],w[MAXM];
int s[MAXM][MAXM];    //s[i][j]表示节点i的第j个儿子节点编号
int s_ind[MAXM];      //s_ind[i]表示节点i的儿子数量
int f[MAXM][MAXN/10];
int F[MAXN/10];
int main()
{
  //freopen("in","r",stdin);
  //freopen("out","w",stdout);
  while(scanf("%d%d",&n,&m)!=EOF)
  {
    n/=10;  //优化
    memset(s_ind,0,sizeof(s_ind));
    memset(F,0,sizeof(F));
    for(int i=1;i<=m;i++)
    {
      scanf("%d%d%d",&v[i],&p[i],&q[i]);
      v[i]/=10; //商品价格为10的倍数，优化
      w[i]=v[i]*p[i];
      if(q[i])
	s[q[i]][s_ind[q[i]]++]=i;
    }

    for(int i=1;i<=m;i++)
    {
      if(q[i])
	continue;
      memset(f[i],0,sizeof(f[i]));
      for(int j=0;j<s_ind[i];j++)
      {
	int cur_son=s[i][j];
	for(int k=n-v[i];k>=v[cur_son];k--)
	  f[i][k]=max(f[i][k],f[i][k-v[cur_son]]+w[cur_son]);
      }

      for(int j=n;j>=v[i];j--)
	for(int k=j;k>=v[i];k--)
	  F[j]=max(F[j],F[j-k]+w[i]+f[i][k-v[i]]);
    }
    printf("%d\n",F[n]*10); //*10是为了还原价格
  }
}

还没结束……就是对于这条题的一点思考，如果每件附件还可以有附件的话，那么题目的做法就有点不一样了，我本来觉得这个题目可以用一种更一般的解法来做，是可以用于递归进行的方法，但是目前我还没有完全看完《背包问题九讲》的一些内容，所以暂时没有用其它方法。但是我在《国家集训队2009论文集浅谈几类背包题》里面，发下最后这题的题解，使用PASCAL写的，而且非常短，里面也用了DFS，所以感觉是可以进一步改进方法使之更具有一般性的。By the way，“金明的预算方案”是NOIP2006年的一道题目。

******<转载说明>******

转载注明：诚实的偷包贼

原文地址：http://blog.csdn.net/fanfank/article/details/9159227

******<转载说明/>******