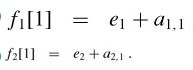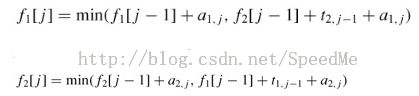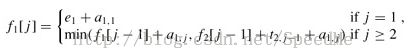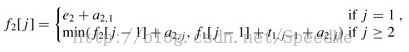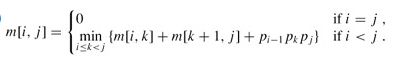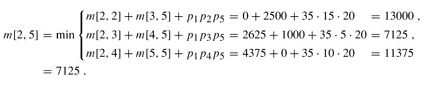《Thinking In Algorithm》13.详解动态规划问题
1. 什么是动态规划
-------------------------------------------
dynamic programming is a method for solving complex problems by breaking them down into simpler subproblems. (通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法)
咦,这不就是分而治之法吗?不,虽然它们的目的是一样的,但它们分解的子问题属性不同。
- 分而治之将问题划分为互不相交的子问题。
- 动态规划不同,动态规划应用于子问题重叠情况,即不同的子问题具有公共的子子问题。
- 最优子结构:如果问题的最优解所包含的子问题的解也是最优的,就称该问题具有最优子结构,即满足最优化原理。
- 无后效性:即某阶段状态一旦确定,就不受这个状态以后决策的影响。也就是说,某状态以后的过程不会影响以前的状态,只与当前状态有关。
- 重叠子问题:即子问题之间是不独立的,一个子问题在下一阶段决策中可能被多次使用到。(该性质并不是动态规划适用的必要条件,但是如果没有这条性质,动态规划算法同其他算法相比就不具备优势)
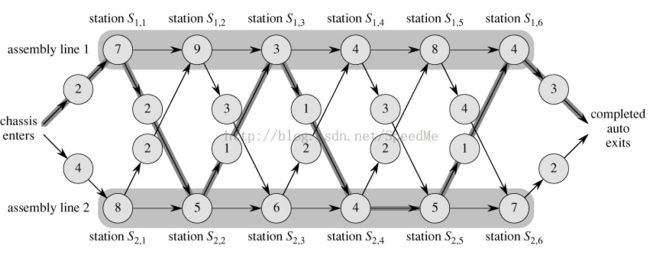
2. 流水线调度问题
- Characterize the structure of an optimal solution. (分析最优解的性质,并刻画其结构特征)
- Recursively define the value of an optimal solution. (递归的定义最优解)
- Compute the value of an optimal solution in a bottom-up fashion. (以自底向上或自顶向下的记忆化方式(备忘录法)计算出最优值)
- Construct an optimal solution from computed information. (根据计算最优值时得到的信息,构造问题的最优解)
-
the fastest way through station S1,j-1 and then directly through stationS1,j, or
-
the fastest way through station S2,j-1, a transfer from line 2 to line 1, and then through stationS1,j.
-
the fastest way through station S2,j-1 and then directly through stationS2,j, or
-
the fastest way through station S1,j-1, a transfer from line 1 to line 2, and then through stationS2,j.
FASTEST-WAY(a, t, e, x, n) 1 f1[1] ← e1 + a1,1 2 f2[1] ←e2 + a2,1 3 for j ← 2 to n 4 do if f1[j - 1] + a1,j ≤ f2[j - 1] + t2,j-1 + a1,j 5 then f1[j] ← f1[j - 1] + a1, j 6 l1[j] ← 1 7 else f1[j] ← f2[j - 1] + t2,j-1 + a1,j 8 l1[j] ← 2 9 if f2[j - 1] + a2,j ≤ f1[j - 1] + t1,j-1 + a2,j 10 then f2[j] ← f2[j - 1] + a2,j 11 l2[j] ← 2 12 else f2[j] ∞ f1[j - 1] + t1,j-1 + a2,j 13 l2[j] ← 1 14 if f1[n] + x1 ≤ f2[n] + x2 15 then f* = f1[n] + x1 16 l* = 1 17 else f* = f2[n] + x2 18 l* = 2
PRINT-STATIONS(l, n) 1 i ← l* 2 print "line " i ", station " n 3 for j ← n downto 2 4 do i ← li[j] 5 print "line " i ", station " j - 1
line 1, station 6
line 2, station 5
line 2, station 4
line 1, station 3
line 2, station 2
line 1, station 1
3 矩阵链乘法
MATRIX-MULTIPLY(A, B)
1 if columns[A] ≠ rows[B]
2 then error "incompatible dimensions"
3 else for i ← 1 to rows[A] // rows[A]
4 do for j ← 1 to columns[B] // col[B]
5 do C[i, j] ← 0
6 for k ← 1 to columns[A] // col[A]
7 do C[i, j] ← C[i, j] + A[i, k] · B[k, j]
8 return C
从上面的代码中,我们可以看出两个矩阵AB相乘,他们的操作次数为rows[A]*col[B]*col[A].知道这一点之后,我们看下面:
- (AB)C = (10×30×5) + (10×5×60) = 1500 + 3000 = 4500 operations
- A(BC) = (30×5×60) + (10×30×60) = 9000 + 18000 = 27000 operations.
- 这下你应该清楚了题意吧。好,那我们下面想想怎么来减少它的次数。依然按照动态规划的算法流程来解决问题:
- 当(A1*A2)*A3时,此时K=2,即表示分界点为A2.
- 当A1*(A2*A3)时,此时K=1,即表示分界点为A1.
MATRIX-CHAIN-ORDER(p) 1 n ← length[p] - 1 2 for i ← 1 to n 3 do m[i, i] ← 0 4 for l ← 2 to n ▹l is the chain length. 5 do for i ← 1 to n - l + 1 6 do j ← i + l - 1 7 m[i, j] ← ∞ 8 for k ← i to j - 1 9 do q ← m[i, k] + m[k + 1, j] + pi-1 pkpj 10 if q < m[i, j] 11 then m[i, j] ← q 12 s[i, j] ← k 13 return m and s解释一下:
// Matrix Ai has dimension p[i-1] x p[i] for i = 1..n
MatrixChainOrder(int p[])
{
// length[p] = n + 1
n = p.length - 1;
// m[i,j] = Minimum number of scalar multiplications (i.e., cost)
// needed to compute the matrix A[i]A[i+1]...A[j] = A[i..j]
// cost is zero when multiplying one matrix
for (i = 1; i <= n; i++)
m[i,i] = 0;
for (L=2; L<=n; L++) { // L is chain length
for (i=1; i<=n-L+1; i++) {
j = i+L-1;
m[i,j] = MAXINT;
for (k=i; k<=j-1; k++) {
// q = cost/scalar multiplications
q = m[i,k] + m[k+1,j] + p[i-1]*p[k]*p[j];
if (q < m[i,j]) {
m[i,j] = q;
s[i,j]=k// s[i,j] = Second auxiliary table that stores k
// k = Index that achieved optimal cost
}
}
}
}
}
PRINT-OPTIMAL-PARENS(s, i, j) 1 if i = j 2 then print "A"i 3 else print "(" 4 PRINT-OPTIMAL-PARENS(s, i, s[i, j]) 5 PRINT-OPTIMAL-PARENS(s, s[i, j] + 1, j) 6 print ")"
public class MatrixOrderOptimization {
protected int[][]m;
protected int[][]s;
public void matrixChainOrder(int[] p) {
int n = p.length - 1;
m = new int[n][n];
s = new int[n][n];
for (int i = 0; i < n; i++) {
m[i] = new int[n];
m[i][i] = 0;
s[i] = new int[n];
}
for (int ii = 1; ii < n; ii++) {
for (int i = 0; i < n - ii; i++) {
int j = i + ii;
m[i][j] = Integer.MAX_VALUE;
for (int k = i; k < j; k++) {
int q = m[i][k] + m[k+1][j] + p[i]*p[k+1]*p[j+1];
if (q < m[i][j]) {
m[i][j] = q;
s[i][j] = k;
}
}
}
}
}
public void printOptimalParenthesizations() {
boolean[] inAResult = new boolean[s.length];
printOptimalParenthesizations(s, 0, s.length - 1, inAResult);
}
void printOptimalParenthesizations(int[][]s, int i, int j, /* for pretty printing: */ boolean[] inAResult) {
if (i != j) {
printOptimalParenthesizations(s, i, s[i][j], inAResult);
printOptimalParenthesizations(s, s[i][j] + 1, j, inAResult);
String istr = inAResult[i] ? "_result " : " ";
String jstr = inAResult[j] ? "_result " : " ";
System.out.println(" A_" + i + istr + "* A_" + j + jstr);
inAResult[i] = true;
inAResult[j] = true;
}
}
}
4. 动态规划原理
【例题1】余数最少的路径。
如图所示,有4个点,分别是A、B、C、D,相邻两点用两条连线C2k,C2k-1(1≤k≤3)表示两条通行的道路。连线上的数字表示道路的长度。定义从A到D的所有路径中,长度除以4所得余数最小的路径为最优路径。
求一条最优路径。
【分析】在这个问题中,如果A的最优取值可以由B的最优取值来确定,而B的最优取值为(1+3) mod 4 = 0,所以A的最优值应为2,而实际上,路径C1-C3-C5可得最优值为(2+1+1) mod 4 = 0,所以,B的最优路径并不是A的最优路径的子路径,也就是说,A的最优取值不是由B的最优取值决定的,即其不满足最优化原理,问题不具有最优子结构的性质。
由此可见,并不是所有的“决策问题”都可以用“动态规划”来解决,运用“动态规划”来处理问题必须满足最优化原理。
4.2 重叠子问题
问题利用递归方法会反复地求解相同的子问题,而不是一直生成新的子问题,我们就成该问题是重叠子问题。
在分治方法中通常就每一步都生成全新的子问题,动态规划就是利用重叠子问题性质:对每个子问题球结一次,将解存入一个表中,当再次需要这个子问题时直接查表,每次查表的代价为常数时间。
4.3 无后效性
它是这样一种性质:某阶段的状态一旦确定,则此后过程的演变不再受此前各种状态及决策的影响,简单的说,就是“未来与过去无关”,当前的状态是此前历史的一个完整总结,此前的历史只能通过当前的状态去影响过程未来的演变。具体地说,如果一个问题被划分各个阶段之后,阶段I中的状态只能由阶段I-1中的状态通过状态转移方程得来,与其它状态没有关系,特别是与未发生的状态没有关系。从图论的角度去考虑,如果把这个问题中的状态定义成图中的顶点,两个状态之间的转移定义为边,转移过程中的权值增量定义为边的权值,则构成一个有向无环加权图,因此,这个图可以进行“拓扑排序”,至少可以按它们拓扑排序的顺序去划分阶段。
简单来说就是在状态i求解时用到状态j而状态j求解时用到状态k…..状态N。
而如果求状态N时有用到了状态i这样求解状态的过程形成了环就没法用动态规划解答了,这也是上面用图论理解动态规划中形成的图无环的原因。
也就是说当前状态是前面状态的完美总结,现在与过去无关。
当然,要是换一个划分状态或阶段的方法就满足无后效性了,这样的问题仍然可以用动态规划解。
动态规划问题还有还多,这里就不一一举例子了,如最长公子序列,背包问题,最有二叉搜索树。之后再添加上去,先把上面两个例子理解了。
不得不说动态规划问题好难啊,我ri。
看下这篇博客吧:最大子数组和