霍夫变换直线检测houghlines及opencv的实现分析
导读:
1. houghlines的算法思想
2. houghlines实现需要考虑的要素
3. houghlines的opencv实现,代码分析
4. houghlines的效率分析,改进
1. houghlines的算法思想
检测直线,houghlines标准算法,不考虑线段,不检测线段端点。
在直角坐标系和极坐标系的对应关系,点、直线在两个坐标系中是对偶关系。
即直角坐标系中的点是极坐标系中的线,直角坐标系中的线是极坐标系中的点。
反过来,也成立。
图像可知看做直角坐标系,检测图像中的直线,可以转化为统计检测极坐标系中的点(r,theta)。

2. houghlines实现需要考虑的因素
hough空间(离散极坐标)的表示
原因:
图像中直线的表示,由斜率和截距表示,而极坐标中用(r, theta)表示.
r = cos(theta)*x + sin(theta)*y
对于点(x0, y0) , 在极坐标中就是一条直线(很多对(r,theta)点):
r = cos(theta)*x0 + sin(theta)*y0
r,theta就是一对hough空间的变量表示。
旋转的theta不容易表示,若将r,theta看成直角坐标空间。
一个点(x0, y0), 就是一个正弦曲线。
r = cos(theta)*x0 + sin(theta)*y0
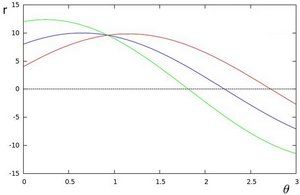
多个点在(r,theta)平面上就是多条正弦曲线,而多条正弦曲线会相交,交点就是直角坐标系中的直线。
接下来,就是要考虑 将r,theta离散化,形成离散化的hough空间,类似于一个mat矩阵/图像,用于统计交点的个数。
opencv取rtho,theta参数作为离散度量,空间分辨率。
则hough空间的大小为:
numangle = cvRound(CV_PI / theta);
numrho = cvRound(((width + height) * 2 + 1) / rho); // 有冗余,在r上留有一定的空白
3. 代码分析
rho: 霍夫空间的r粒度大小
theta: 旋转角度的粒度
threshold:直线上有多少个点的阈值
lines:输出lines结果
4. 效率分析
houghlines的计算效率比较低O(n*n*m),耗时较长,而且没有检测出直线的端点。
改进
统计概论霍夫直线检测houghlinesP是一个改进,不仅执行效率较高,而且能检测到直线的两个端点。
思想:
先随机检测出一部分直线,然后将直线上点的排查掉,再进行其他直线的检测
1. 首先仅统计图像中非零点的个数,对于已经确认是某条直线上的点就不再变换了。
2. 对所以有非零点逐个变换到霍夫空间
a. 并累加到霍夫统计表(图像)中,并统计最大值
b. 最大值与阈值比较,小于阈值,则继续下一个点的变换
c. 若大于阈值,则有一个新的直线段要产生了
d. 计算直线上线段的端点、长度,如果符合条件,则保存此线段,并mark这个线段上的点不参与其他线段检测的变换
1. houghlines的算法思想
2. houghlines实现需要考虑的要素
3. houghlines的opencv实现,代码分析
4. houghlines的效率分析,改进
1. houghlines的算法思想
检测直线,houghlines标准算法,不考虑线段,不检测线段端点。
在直角坐标系和极坐标系的对应关系,点、直线在两个坐标系中是对偶关系。
即直角坐标系中的点是极坐标系中的线,直角坐标系中的线是极坐标系中的点。
反过来,也成立。
图像可知看做直角坐标系,检测图像中的直线,可以转化为统计检测极坐标系中的点(r,theta)。

2. houghlines实现需要考虑的因素
hough空间(离散极坐标)的表示
原因:
图像中直线的表示,由斜率和截距表示,而极坐标中用(r, theta)表示.
r = cos(theta)*x + sin(theta)*y
对于点(x0, y0) , 在极坐标中就是一条直线(很多对(r,theta)点):
r = cos(theta)*x0 + sin(theta)*y0
r,theta就是一对hough空间的变量表示。
旋转的theta不容易表示,若将r,theta看成直角坐标空间。
一个点(x0, y0), 就是一个正弦曲线。
r = cos(theta)*x0 + sin(theta)*y0
直角坐标系中的一点
对应于r-theta空间的一条正弦曲线多个点在(r,theta)平面上就是多条正弦曲线,而多条正弦曲线会相交,交点就是直角坐标系中的直线。
直角坐标系中的一条直线上的三个点
对应于r-theta空间中三条曲线,并交于一点
接下来,就是要考虑 将r,theta离散化,形成离散化的hough空间,类似于一个mat矩阵/图像,用于统计交点的个数。
opencv取rtho,theta参数作为离散度量,空间分辨率。
则hough空间的大小为:
numangle = cvRound(CV_PI / theta);
numrho = cvRound(((width + height) * 2 + 1) / rho); // 有冗余,在r上留有一定的空白
3. 代码分析
rho: 霍夫空间的r粒度大小
theta: 旋转角度的粒度
threshold:直线上有多少个点的阈值
lines:输出lines结果
linesMax:lines的最大个数
static void
icvHoughLinesStandard( const CvMat* img, float rho, float theta,
int threshold, CvSeq *lines, int linesMax )
{
cv::AutoBuffer<int> _accum, _sort_buf;
cv::AutoBuffer<float> _tabSin, _tabCos;
const uchar* image;
int step, width, height;
int numangle, numrho;
int total = 0;
float ang;
int r, n;
int i, j;
float irho = 1 / rho;
double scale;
CV_Assert( CV_IS_MAT(img) && CV_MAT_TYPE(img->type) == CV_8UC1 );
image = img->data.ptr;
step = img->step;
width = img->cols;
height = img->rows;
numangle = cvRound(CV_PI / theta); // 霍夫空间,角度方向的大小
numrho = cvRound(((width + height) * 2 + 1) / rho); // r的空间范围
_accum.allocate((numangle+2) * (numrho+2));
_sort_buf.allocate(numangle * numrho);
_tabSin.allocate(numangle);
_tabCos.allocate(numangle);
int *accum = _accum, *sort_buf = _sort_buf;
float *tabSin = _tabSin, *tabCos = _tabCos;
memset( accum, 0, sizeof(accum[0]) * (numangle+2) * (numrho+2) );
for( ang = 0, n = 0; n < numangle; ang += theta, n++ ) // 计算正弦曲线的准备工作,查表
{
tabSin[n] = (float)(sin(ang) * irho);
tabCos[n] = (float)(cos(ang) * irho);
}
// stage 1. fill accumulator
for( i = 0; i < height; i++ )
for( j = 0; j < width; j++ )
{
if( image[i * step + j] != 0 ) // 将每个非零点,转换为霍夫空间的离散正弦曲线,并统计。
for( n = 0; n < numangle; n++ )
{
r = cvRound( j * tabCos[n] + i * tabSin[n] );
r += (numrho - 1) / 2;
accum[(n+1) * (numrho+2) + r+1]++;
}
}
// stage 2. find local maximums // 霍夫空间,局部最大点,采用四邻域判断,比较。(也可以使8邻域或者更大的方式), 如果不判断局部最大值,同时选用次大值与最大值,就可能会是两个相邻的直线,但实际上是一条直线。选用最大值,也是去除离散的近似计算带来的误差,或合并近似曲线。
for( r = 0; r < numrho; r++ )
for( n = 0; n < numangle; n++ )
{
int base = (n+1) * (numrho+2) + r+1;
if( accum[base] > threshold &&
accum[base] > accum[base - 1] && accum[base] >= accum[base + 1] &&
accum[base] > accum[base - numrho - 2] && accum[base] >= accum[base + numrho + 2] )
sort_buf[total++] = base;
}
// stage 3. sort the detected lines by accumulator value // 由点的个数排序,依次找出哪些最有可能是直线
icvHoughSortDescent32s( sort_buf, total, accum );
// stage 4. store the first min(total,linesMax) lines to the output buffer
linesMax = MIN(linesMax, total);
scale = 1./(numrho+2);
for( i = 0; i < linesMax; i++ ) // 依据霍夫空间分辨率,计算直线的实际r,theta参数
{
CvLinePolar line;
int idx = sort_buf[i];
int n = cvFloor(idx*scale) - 1;
int r = idx - (n+1)*(numrho+2) - 1;
line.rho = (r - (numrho - 1)*0.5f) * rho;
line.angle = n * theta;
cvSeqPush( lines, &line );
}
}
4. 效率分析
houghlines的计算效率比较低O(n*n*m),耗时较长,而且没有检测出直线的端点。
改进
统计概论霍夫直线检测houghlinesP是一个改进,不仅执行效率较高,而且能检测到直线的两个端点。
思想:
先随机检测出一部分直线,然后将直线上点的排查掉,再进行其他直线的检测
1. 首先仅统计图像中非零点的个数,对于已经确认是某条直线上的点就不再变换了。
2. 对所以有非零点逐个变换到霍夫空间
a. 并累加到霍夫统计表(图像)中,并统计最大值
b. 最大值与阈值比较,小于阈值,则继续下一个点的变换
c. 若大于阈值,则有一个新的直线段要产生了
d. 计算直线上线段的端点、长度,如果符合条件,则保存此线段,并mark这个线段上的点不参与其他线段检测的变换