C/C++ 图像处理（8）------图像の柱面投影算法

    图像的柱面投影算法，在360°环形全景应用中几乎一定会用到。而为何要用该算法，可以参考下图:

    从图像中可以看到，該环形全景设备由八个摄像头环形排列而成（需注意环形全景的形态并不固定，摄像头的个数不一定是八个，甚至只有一个摄像头在一直匀速转圈也是可以的）。每个摄像头所拍摄的画面为其前方的实线段区域，为了之后能进行图像的拼接，相邻摄像头之间必须要有图像的重合区域，如上图的红色线段部分（如果能保证刚刚好相接也可以，不过结构难度太高）。

    从不同摄像头的重合区域可以看到，由于摄像头的朝向不同，重合部分图像中的物体并不满足视觉一致性的要求，因此需要将图像进行投影，使其满足图像的一致性要求，为后面的拼接做准备（视觉一致性是全景应用最为关键的问题，无论是柱环形全景还是球形全景，都无法避免，只是所选的投影模型不同罢了）。在环形全景中，一般选择柱面投影算法，将图像分别投影到以 像素焦距+摄像头与圆心距离 为半径的圆柱上。投影后的图像为上图摄像头前方的圆弧。从圆弧上看，图像的重合部分已经满足视觉一致性的要求，可以做拼接。而如何去投影就是本文要介绍的。

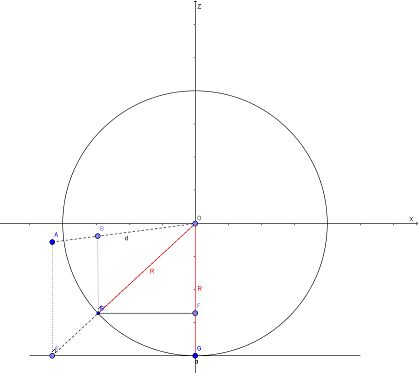
    柱面投影的数学模型相对比较简单，把观测点定在圆柱体的中心，图像的像素焦距+摄像头与圆心距离 为圆柱体的半径，则摄像头所拍摄的图像与圆柱体相切。图像上的一点Q与观测点连线，该连线与圆柱面的交点点Q'为图像点Q在柱面上的投影，我们需要做的就是求出点Q(x,y)与点Q'(x',y')之间的换算关系。先看看下图:

    该图的实线部分为投影模型的俯视图，下方的线段a为待投影的图像，圆为圆柱切面，O为观测点。而虚线部分为Y轴方向上的辅助线。现在设A为图像上的任意一点，其坐标为(x,y,z),其中z=-R，则其在x-z坐标系上的投影A'的坐标为(x，-R)。B为我们要求的点A在圆柱面上的投影点，其坐标为(x',y',z')，则其在x-z坐标系上的投影点B'的坐标为(x',z')。

    由于△0BB'与△OAA'相似，△0B'F与△OA'G相似

    则有BB'=kAA',B'F=kA'G，OF=kR(k<1)

    则kx=x',ky=y'

    又OF²+B'F²=R²

    故k²R²+k²x²=R²

    

    又x'=kx,y'=ky

    故

    

    

    由于一般来说图像以左上角为坐标原点，而上面公式中的坐标系以图像的中心为坐标原点，所以在实际图像的计算中，上面的计算公式换为

    

    

    有了上面的公式，便可计算出图像的柱面投影结果。这里需要注意的是我们把x和y写在了等式的左边而x',y'写在了右边，这样做是为了方便我们后面进行插值计算。为什么要这么做可以看下面两张图片

 

    左边图像为待投影图像，右边为直接投影的结果，由于投影后的图像点坐标未必为整数，而图像的坐标需要为整数，所以必将造成误差。表现在右边图像上就是图像有很多显而易见的毛刺。而我们进行双线性插值之后的投影图像如下

    可以看到，其毛刺得到了一定的抑制。上面的图像还说明了经过柱面投影的图像会比原来的图像宽度小，具体小多少跟R有关，由于比较简单，在这里不再给出推导的过程。以上投影过程的主要代码如下

void DealWithImgData(BYTE *srcdata, BYTE *drcdata,int width,int height)//参数一为原图像的数据区首指针，参数二为投影后图像的数据区首指针，参数三为图像的宽，参数四为图像的高
{
	//双线性插值算法
	int i_original_img_hnum, i_original_img_wnum;//目标点坐标
	double distance_to_a_y, distance_to_a_x;//在原图像中与a点的水平距离  
	int original_point_a, original_point_b, original_point_c, original_point_d;

	int l_width = WIDTHBYTES(width* 24);//计算位图的实际宽度并确保它为4byte的倍数
	int drcpoint;
	double R = 1200;//像素距离
	double x, y;
	for (int hnum = 0; hnum < height; hnum++)
	{
		for (int wnum = 0; wnum < width; wnum++)
		{
			drcpoint = l_width*hnum + wnum * 3;//数组位置偏移量，对应于图像的各像素点RGB的起点
			//柱面投影
			double k = R / sqrt(R*R + (wnum- width / 2) * (wnum - width / 2));
			x = (wnum - width / 2) / k + width / 2;
			y = (hnum - height / 2) / k + height / 2;
			if (x >= 0 && y >= 0 && x < width && y < height)
			{
				/***********双线性插值算法***********/
				i_original_img_hnum = y;
				i_original_img_wnum = x;
				distance_to_a_y = y - i_original_img_hnum;
				distance_to_a_x = x - i_original_img_wnum;//在原图像中与a点的垂直距离  

				original_point_a = i_original_img_hnum*l_width + i_original_img_wnum * 3;//数组位置偏移量，对应于图像的各像素点RGB的起点,相当于点A    
				original_point_b = original_point_a + 3;//数组位置偏移量，对应于图像的各像素点RGB的起点,相当于点B  
				original_point_c = original_point_a + l_width;//数组位置偏移量，对应于图像的各像素点RGB的起点,相当于点C   
				original_point_d = original_point_c + 3;//数组位置偏移量，对应于图像的各像素点RGB的起点,相当于点D  

				if (i_original_img_hnum == height - 1)
				{
					original_point_c = original_point_a;
					original_point_d = original_point_b;
				}
				if (i_original_img_wnum == width - 1)
				{
					original_point_a = original_point_b;
					original_point_c = original_point_d;
				}

				drcdata[drcpoint + 0] =
					srcdata[original_point_a + 0] * (1 - distance_to_a_x)*(1 - distance_to_a_y) +
					srcdata[original_point_b + 0] * distance_to_a_x*(1 - distance_to_a_y) +
					srcdata[original_point_c + 0] * distance_to_a_y*(1 - distance_to_a_x) +
					srcdata[original_point_c + 0] * distance_to_a_y*distance_to_a_x;
				drcdata[drcpoint + 1] =
					srcdata[original_point_a + 1] * (1 - distance_to_a_x)*(1 - distance_to_a_y) +
					srcdata[original_point_b + 1] * distance_to_a_x*(1 - distance_to_a_y) +
					srcdata[original_point_c + 1] * distance_to_a_y*(1 - distance_to_a_x) +
					srcdata[original_point_c + 1] * distance_to_a_y*distance_to_a_x;
				drcdata[drcpoint + 2] =
					srcdata[original_point_a + 2] * (1 - distance_to_a_x)*(1 - distance_to_a_y) +
					srcdata[original_point_b + 2] * distance_to_a_x*(1 - distance_to_a_y) +
					srcdata[original_point_c + 2] * distance_to_a_y*(1 - distance_to_a_x) +
					srcdata[original_point_c + 2] * distance_to_a_y*distance_to_a_x;
				/***********双线性插值算法***********/
			}
		}
	}
}