数据结构----深度优先搜索的应用
1.深度优先搜索
用通俗一点的话即从某一路口出发一直沿着某一条走到底直到没路时,返回到一个有新路的路口,沿着新路继续走,依次反复直到无路可走!
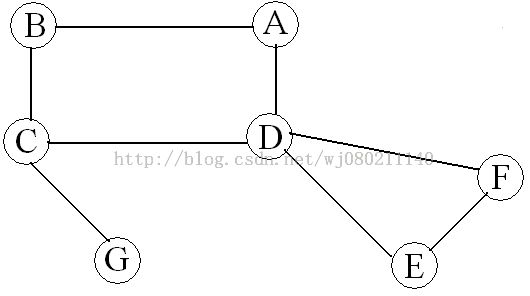
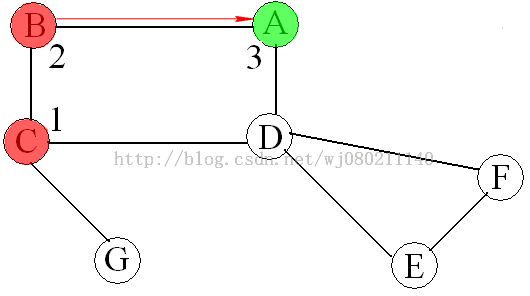
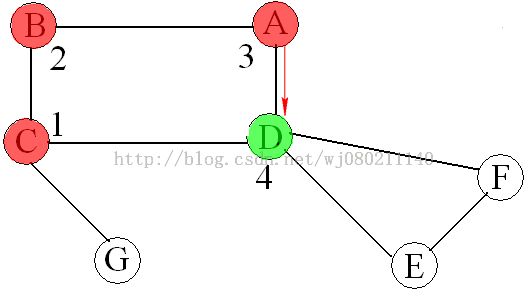
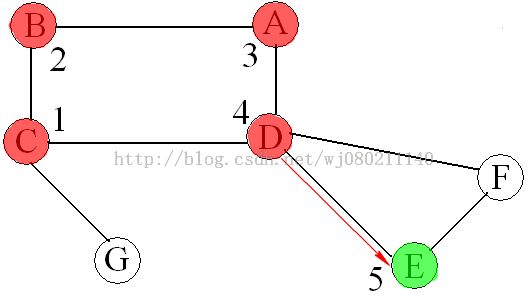
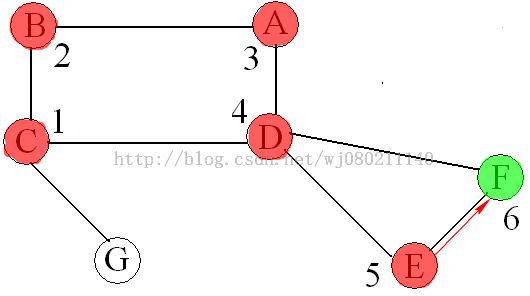
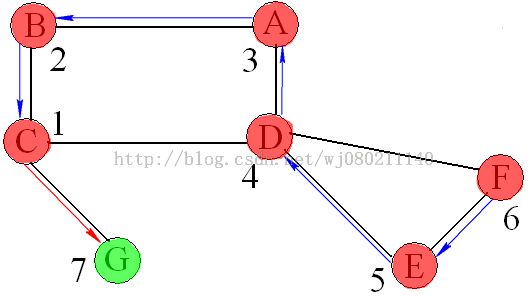
下面用《数据结构与算法分析(C语言描述)》中图9-62说明一下深度优先搜索算法:
说明:①从顶点C开始进行深度优先搜索
②绿色圆斑表示当前访问顶点,红色圆斑表示已经访问过的顶点,数字表示先序编号
③红色箭头表示正向边、搜索方向,蓝色箭头表示回溯过程,未出现过箭头的边为背向边
④与书中得到的深度优先搜索树不一致是由于进行下一次搜索时选取的相邻顶点不一致造成的,本文中按字母顺序
2.双连通性
在网上看到一个比书中更好的定义:
割点集合和点连通度:在一个无向连通图中,如果有一个顶点集合,删除该顶点集合以及这个集合所有顶点相关联的边以后,原图变成多个连通块,就称该点集合为割点集合,最小割点集合的顶点数目称为顶点连通度。类似地可以定义割边集合和边连通度。
双连通性:如果一个无向图的点连通度或边连通度大于1,则称该图为双联通的。
Num:深度优先先序编号
Low:在生成的深度优先树中,每个顶点通过零条边或多条正向边(红色箭头表示)且可能还有一条背向边(无箭头边CD、DA)可以达到最小Num值。
根据上面定义Low(v)可以是
①Num(v)------零条边
②所有背向边(v,w)中最低的Num(w)-------一条背向边
③所有正向边(v,w)中最低的Low(w)-------一条正向边+(N条正向边+一条背向边)
割点判断条件:
①根节点:当且仅当它多于一个儿子
②非根节点v:Low(w)>=Num(v),w为v的某一个儿子
3.代码
3.1邻接矩阵表示图
主函数
Graphic_Matrix g_matrix = new Graphic_Matrix(10, false);
//添加顶点
//
g_matrix.AddVertex(new Vertex("A"));
g_matrix.AddVertex(new Vertex("B"));
g_matrix.AddVertex(new Vertex("C"));
g_matrix.AddVertex(new Vertex("D"));
g_matrix.AddVertex(new Vertex("E"));
g_matrix.AddVertex(new Vertex("F"));
g_matrix.AddVertex(new Vertex("G"));
//添加边
//
g_matrix.AddEdge(new Vertex("A"), new Vertex("B"));
g_matrix.AddEdge(new Vertex("A"), new Vertex("D"));
g_matrix.AddEdge(new Vertex("B"), new Vertex("C"));
g_matrix.AddEdge(new Vertex("C"), new Vertex("D"));
g_matrix.AddEdge(new Vertex("C"), new Vertex("G"));
g_matrix.AddEdge(new Vertex("D"), new Vertex("E"));
g_matrix.AddEdge(new Vertex("D"), new Vertex("F"));
g_matrix.AddEdge(new Vertex("E"), new Vertex("F"));
g_matrix.PrintVertexList();
g_matrix.PrintAdjacencyMat();
TableBioC table1 = new TableBioC(g_matrix.Size);
Vertex start_vertex = new Vertex("A");
//AssignNum(g_matrix, table1, start_vertex);
//AssignLow(g_matrix, table1, start_vertex);
FindArt(g_matrix, table1, start_vertex);
TableBioC.PrintTable(table1, g_matrix);
PrintArt(g_matrix, table1, start_vertex);深度优先先序编号幅值函数
private static void AssignNum(Graphic_Matrix g_matrix,TableBioC table, Vertex current_vertex)
{
Vertex adjacent_vertex;
int current_index = 0;
current_index = g_matrix.GetIndex(current_vertex); //当前顶点的内部编号,并记录其num,修改访问标志
table.num[current_index] = table.count++;
table.is_visited[current_index] = true;
for (int i = 0; i < g_matrix.Size; i++)
{
if (g_matrix.AdjacencyMat[current_index, i] != 0)
{
if (!table.is_visited[i]) //该相邻点是否被访问过
{
adjacent_vertex = g_matrix.VertexList[i];
table.parent[i] = new Vertex(current_vertex.Name);
AssignNum(g_matrix, table, adjacent_vertex);
}
}
}
}Low值计算函数
private static void AssignLow(Graphic_Matrix g_matrix, TableBioC table, Vertex current_vertex)
{
Vertex adjacent_vertex;
int current_index = 0;
current_index = g_matrix.GetIndex(current_vertex);
table.low[current_index] = table.num[current_index]; //规则1.num(v)
for (int i = 0; i < g_matrix.Size; i++)
{
if (g_matrix.AdjacencyMat[current_index, i] != 0)
{
if (table.num[i] > table.num[current_index]) //正向边
{
adjacent_vertex = g_matrix.VertexList[i];
AssignLow(g_matrix, table, adjacent_vertex);
table.low[current_index] = Math.Min(table.low[current_index], table.low[i]); //规则2.正向(v,w)最低low(w)
}
else
{
if (table.parent[current_index].Name != g_matrix.VertexList[i].Name)
{
table.low[current_index] = Math.Min(table.low[current_index], table.num[i]); //规则3.背向边(v,w)最低num(w)
}
}
}
}
}两者合一
private static void FindArt(Graphic_Matrix g_matrix, TableBioC table, Vertex current_vertex)
{
Vertex adjacent_vertex;
int current_index = 0;
current_index = g_matrix.GetIndex(current_vertex);
table.num[current_index] = table.count++;
table.low[current_index] = table.num[current_index]; //rule 1
table.is_visited[current_index] = true;
for (int i = 0; i < g_matrix.Size; i++)
{
if (g_matrix.AdjacencyMat[current_index, i] != 0)
{
if (!table.is_visited[i])
{
adjacent_vertex = g_matrix.VertexList[i];
table.parent[i] = new Vertex(current_vertex.Name);
FindArt(g_matrix, table, adjacent_vertex);
table.low[current_index] = Math.Min(table.low[current_index], table.low[i]); //rule 2
}
else
{
if (table.parent[current_index] !=null&& table.parent[current_index].Name != g_matrix.VertexList[i].Name)
{
table.low[current_index] = Math.Min(table.low[current_index], table.num[i]); //rule 3
}
}
}
}
}
打印割点函数(书中给出的伪代码会多次输出割点且对于根节点情况为进行特殊考虑)
private static void PrintArt(Graphic_Matrix g_matrix, TableBioC table, Vertex start_vertex)
{
int start_index = g_matrix.GetIndex(start_vertex), count = 0;
Vertex current_vertex;
//根节点
//
for (int i = 0; i < table.table_size; i++)
{
if (i != start_index)
{
if (table.parent[i].Name == start_vertex.Name)
{
count++;
}
}
}
if (count > 1)
{
Console.Write("{0}是一个割点!", start_vertex.Name);
}
//非根节点
//
for (int i = 0; i < table.table_size; i++)
{
if (i != start_index)
{
current_vertex = g_matrix.GetVertex(i);
for (int j = 0; j < table.table_size; j++)
{
if (j != start_index)
{
if (table.parent[j].Name == current_vertex.Name)
{
if (table.low[j] >= table.num[i])
Console.WriteLine("{0}是一个割点!", current_vertex.Name);
}
}
}
}
}
}
3.2邻接表表示图
主函数
Graphic_List g_list = new Graphic_List(10, false);
//添加顶点
//
g_list.AddVertex(new Vertex("A"));
g_list.AddVertex(new Vertex("A"));
g_list.AddVertex(new Vertex("B"));
g_list.AddVertex(new Vertex("C"));
g_list.AddVertex(new Vertex("D"));
g_list.AddVertex(new Vertex("E"));
g_list.AddVertex(new Vertex("F"));
g_list.AddVertex(new Vertex("G"));
//添加边
//
g_list.AddEdge(new Vertex("A"), new Vertex("B"));
g_list.AddEdge(new Vertex("A"), new Vertex("D"));
g_list.AddEdge(new Vertex("B"), new Vertex("C"));
g_list.AddEdge(new Vertex("C"), new Vertex("D"));
g_list.AddEdge(new Vertex("C"), new Vertex("G"));
g_list.AddEdge(new Vertex("D"), new Vertex("E"));
g_list.AddEdge(new Vertex("D"), new Vertex("F"));
g_list.AddEdge(new Vertex("E"), new Vertex("F"));
//打印邻接表
//
g_list.PrintGraphicList();
TableBioC table2 = new TableBioC(g_list.Items.Count);
//AssignNum(g_list, table2, start_vertex);
//AssignLow(g_list, table2, start_vertex);
FindArt(g_list, table2, start_vertex);
TableBioC.PrintTable(table2, g_list);
PrintArt(g_list, table2, start_vertex);
Console.ReadKey();
深度优先先序编号幅值函数
private static void AssignNum(Graphic_List g_list, TableBioC table, Vertex current_vertex)
{
Vertex adjacent_vertex;
int current_index = 0,adjacent_index=0;
current_index = g_list.GetIndex(current_vertex);
current_vertex = g_list.GetVertex(current_index);
table.num[current_index] = table.count++;
table.is_visited[current_index] = true;
while (current_vertex.NextVertex != null)
{
adjacent_vertex = new Vertex(current_vertex.NextVertex.Name);
adjacent_index = g_list.GetIndex(adjacent_vertex);
if (!table.is_visited[adjacent_index])
{
table.parent[adjacent_index] = new Vertex(g_list.Items[current_index].Name);
AssignNum(g_list, table, adjacent_vertex);
}
current_vertex = current_vertex.NextVertex;
}
}
Low值计算函数
private static void AssignLow(Graphic_List g_list, TableBioC table, Vertex current_vertex)
{
Vertex adjacent_vertex;
int current_index = 0,adjacent_index=0;
current_index = g_list.GetIndex(current_vertex);
current_vertex = g_list.GetVertex(current_index);
table.low[current_index] = table.num[current_index]; //rule1 low(v)=num(v)
while (current_vertex.NextVertex != null)
{
adjacent_vertex = new Vertex(current_vertex.NextVertex.Name);
adjacent_index = g_list.GetIndex(adjacent_vertex);
if (table.num[adjacent_index] > table.num[current_index])
{
AssignLow(g_list, table, adjacent_vertex);
table.low[current_index] = Math.Min(table.low[current_index], table.low[adjacent_index]); //rule3 low(v)=min(low(v),low(w))
}
else
{
if (table.parent[current_index].Name != adjacent_vertex.Name)
{
table.low[current_index] = Math.Min(table.low[current_index], table.num[adjacent_index]); //rule2 low(v)=min(low(v),num(w))
}
}
current_vertex = current_vertex.NextVertex;
}
}
两者合一
private static void FindArt(Graphic_List g_list, TableBioC table, Vertex current_vertex)
{
Vertex adjacent_vertex;
int current_index = 0, adjacent_index = 0;
current_index = g_list.GetIndex(current_vertex);
current_vertex = g_list.GetVertex(current_index);
table.low[current_index]=table.num[current_index] = table.count++;
table.is_visited[current_index] = true;
while (current_vertex.NextVertex != null)
{
adjacent_vertex = new Vertex(current_vertex.NextVertex.Name);
adjacent_index = g_list.GetIndex(adjacent_vertex);
if (!table.is_visited[adjacent_index])
{
table.parent[adjacent_index] = new Vertex(g_list.Items[current_index].Name);
FindArt(g_list, table, adjacent_vertex);
table.low[current_index] = Math.Min(table.low[current_index], table.low[adjacent_index]);
}
else
{
if (table.parent[current_index]!=null&&table.parent[current_index].Name != adjacent_vertex.Name)
{
table.low[current_index] = Math.Min(table.low[current_index], table.num[adjacent_index]); //rule2 low(v)=min(low(v),num(w))
}
}
current_vertex = current_vertex.NextVertex;
}
}
打印割点函数
private static void PrintArt(Graphic_List g_list, TableBioC table, Vertex start_vertex)
{
int start_index = g_list.GetIndex(start_vertex),count=0;
Vertex current_vertex;
//根节点
//
for (int i = 0; i < table.table_size; i++)
{
if (i != start_index)
{
if (table.parent[i].Name == start_vertex.Name)
{
count++;
}
}
}
if (count > 1)
{
Console.Write("{0}是一个割点!", start_vertex.Name);
}
//非根节点
//
for (int i = 0; i < table.table_size; i++)
{
if (i != start_index)
{
current_vertex=g_list.GetVertex(i);
for (int j = 0; j < table.table_size; j++)
{
if (j != start_index)
{
if (table.parent[j].Name == current_vertex.Name)
{
if (table.low[j] >= table.num[i])
Console.WriteLine("{0}是一个割点!", current_vertex.Name);
}
}
}
}
}
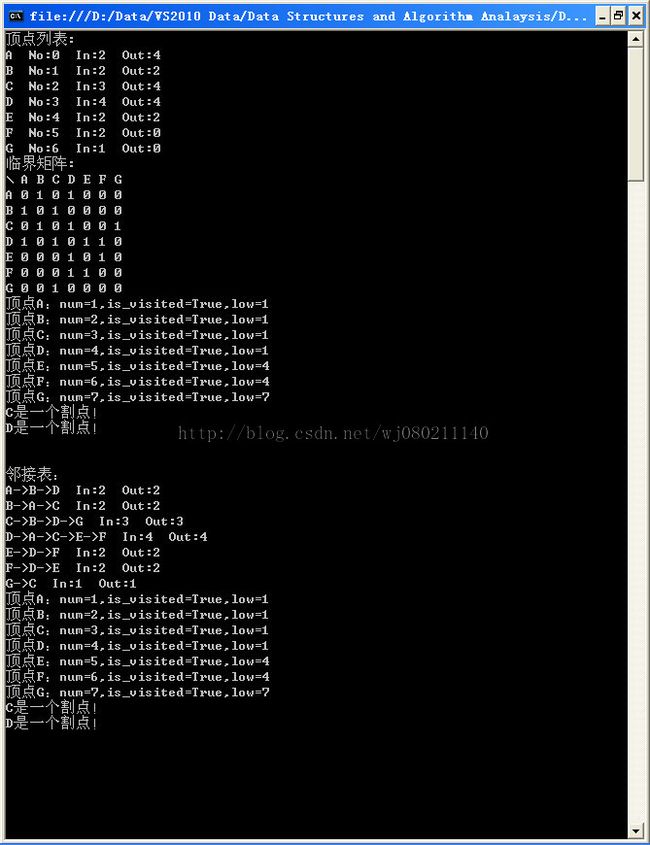
}运行结果: