《数据结构与算法分析》二项队列详解

前言：

      补上这篇博客，就补完一半了。

我的github：

我实现的代码全部贴在我的github中，欢迎大家去参观。

https://github.com/YinWenAtBIT

介绍：

定义：

     二项队列不同于左式堆和二叉堆等优先队列的实现之处在于，一个二项队列不是一棵堆序的树，而是堆序树的集合，即森林。堆序树中的每棵树都是由约束形式的，叫做二项树。每一个高度上至多存在一棵二项树。高度为0的二项树是一颗单节点树，高度为k的二项树Bk通过将一棵二项树Bk-1附接到另一颗二项树Bk-1的根上而构成。下图显示二项树B0，B1，B2，B3以及B4。

二项队列的复杂度

        左堆的合并，插入，删除最小的时间复杂度为O(logN)。二项队列就是为了对这些结果进一步提高的一种数据结构。利用二项队列，这三种操作的最坏时间复杂度为O(logN)，但是插入的平均时间复杂度为O(1)。

基本操作：
合并：
二项队列的合并操作可以看做一个简单的二进制加法运算，从低位运算到高位。首先是两个队列的B0相加，如果两个队列都存在B0（二进制为1），因此将两个B0合并成一个B1树，生成的B1树当做进位，参与下一步的B1运算，直到运算到最高位结束。

删除最小值/最大值：

删除最小值首先要做的事情就是找到最小值。那么只要寻找二项队列对应的每一刻Bk树的根节点中的最小值即可。然后把拥有最小值的Bk树删去根节点。此时剩下的树为B0，B1...Bk-1树。这些树构成一个新的二项队列，然后调用上述的合并操作，既可以完成删除操作。

插入：

插入操作等同于合并操作，非常好完成。

编码实现：

二项队列定义：

在对二项队列编码之前，需要明白如何表示二项队列。因为二项队列的根节点所指向的节点可能是无限的，所以不能像二叉树那样使用两个指针来指向两个儿子（这里有无数个儿子）。

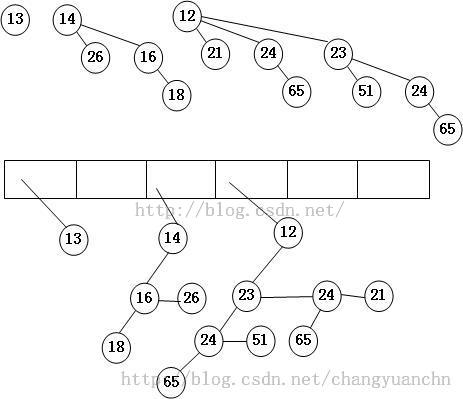
具体的表示方式如下图所示：

第一张图代表我们画出来的二项队列。

第二张图上半部分的数组是指向树节点的指针，即指向Bk的根节点。

每个树节点有三个元素，Element，Leftchild， NextSibling。

其中NextSibling指的是和它本身同级的兄弟。如第一张图中的B3，

12没有同级兄弟，21,24,23互为同级兄弟，65,51,24互为同级兄弟。

那么Leftchild元素指向谁呢，当然是指向有最多孩子的节点，提取出来就是B2的23节点了。

理解了这里，在看第二张图想必会明白多了。

明白了如何表示二项队列之后，就可以开始编码实现了，.h文件如下：

#ifndef _BINOMIAL_QUEUE
#define _BINOMIAL_QUEUE

struct BinNode;
struct Collection;

typedef int ElementType;
typedef struct Collection * BinQueue;
typedef struct BinNode * Position;
typedef struct BinNode * BinTree;

#define MaxSize 30
#define Capacity 4294967296

BinQueue initialize();
bool isEmpty(BinQueue H);
bool isFUll(BinQueue H);
void insert(ElementType X, BinQueue H);
int findMin(BinQueue H);
void destroy(BinQueue H);
BinQueue merge(BinQueue H1, BinQueue H2);
ElementType DeleteMin(BinQueue H);

void PrintTree(BinTree T, int depth);
void PrintDepth(ElementType A, int depth);

struct BinNode
{
	ElementType Element;
	Position leftChild;
	Position nextSibling;

};

struct Collection
{
	int currentSize;
	BinTree theTrees[MaxSize];
};

#endif

其中MaxSize是我自己随意定下来的，2^30次方可以存下不少数据了。这样也方便我计算最大的容量Capacity。

初始化：

BinQueue initialize()
{
	BinQueue H = (BinQueue)calloc(1, sizeof(struct Collection));
	if(H == NULL)
	{
		fprintf(stderr, "not enough memory");
		exit(1);
	}
	H->currentSize = 0;
	return H;
}

合并：

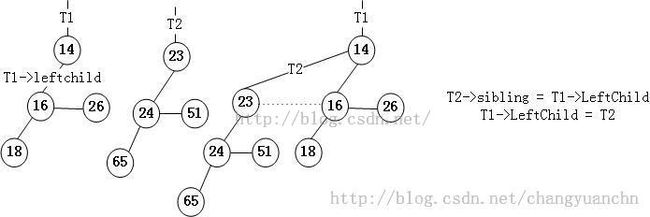
合并操作的主要内容就是做二进制加法运算，使用switch来进行判断。具体到两个Bk树的合并非常的简单，如下图所示：

然较小的根节点变成新的根，另一个Bk成为它的左孩子，它原来的左孩子成为另一个Bk根节点的兄弟。

BinQueue merge(BinQueue H1, BinQueue H2)
{
	BinTree T1, T2, Carry = NULL;
	int i, j;

	if(H1->currentSize + H2->currentSize > Capacity)
	{
		fprintf(stderr, "out of space");
		exit(1);
	}
	H1->currentSize += H2->currentSize;

	for(i =0, j =1; j<= H1->currentSize; i++, j*=2)
	{
		T1 = H1->theTrees[i];
		T2 = H2->theTrees[i];

		switch(!!T1 + 2*!!T2 + 4*!!Carry)
		{
		case 0:/* not Trees*/
		case 1:/* only H1 */
			break;

		case 2: /*only H2 */
			H1->theTrees[i] = T2;
			H2->theTrees[i] = NULL;
			break;

		case 4: /* only carry */
			H1->theTrees[i] = Carry;
			Carry = NULL;
			break;

		case 3: /* H1 and H2 */
			Carry = CombineTrees(T1, T2);
			H1->theTrees[i] = H2->theTrees[i] = NULL;
			break;
		case 5: /* H1 and Cartry */
			Carry = CombineTrees(T1, Carry);
			H1->theTrees[i] = NULL;
			break;
		case 6: /* H2 and Carry */
			Carry = CombineTrees(T2, Carry);
			H2->theTrees[i] = NULL;
			break;
		case 7: /* H1 and H2 and Carry */
			H1->theTrees [i] = Carry;
			Carry = CombineTrees(T1, T2);
			H2->theTrees[i] = NULL;
			break;

		}
	}
	return H1;
}


BinTree CombineTrees(BinTree T1, BinTree T2)
{
	if(T1->Element > T2->Element)
		return CombineTrees(T2, T1);

	T2->nextSibling = T1->leftChild;
	T1->leftChild = T2;
	return T1;
}

插入：

void insert(ElementType X, BinQueue H)
{
	BinQueue temp = initialize();
	BinTree newone = (BinTree)malloc(sizeof(struct BinNode));
	if(newone == NULL)
	{
		fprintf(stderr, "out of space");
		exit(1);
	}
	newone ->Element =X;
	newone->leftChild = newone->nextSibling = NULL;
	
	temp ->currentSize =1;
	temp->theTrees[0] = newone;

	merge(H, temp);
	free(temp); 
}

删除最小值：

先寻找到最小值所对应的指针编号，然后进行删除操作：

int findMin(BinQueue H)
{
	int i, min;
	ElementType minvalue = 0x7FFFFFFF;

	if(isEmpty(H))
		return NULL;

	for(i =0; i<MaxSize; i++)
	{
		if(H->theTrees[i])
			if(H->theTrees[i]->Element <minvalue)
			{
				minvalue = H->theTrees[i]->Element;
				min = i;
			}
	}
	return min;
}

在删除操作的时候要注意二项队列当前储存数据容量的变化。构成新的二项队列是从大往小构成的。先是Bk-1，最后B0。

ElementType DeleteMin(BinQueue H)
{
	int i;
	if(isEmpty(H))
	{
		fprintf(stderr, "empty\n");
		exit(1);
	}
	int min = findMin(H);
	ElementType minValue;

	BinTree DeletedTree, OldTree;
	BinQueue DeletedQueue;

	OldTree = H->theTrees[min];
	minValue = OldTree ->Element;
	DeletedTree = OldTree ->leftChild;
	free (OldTree);
	DeletedQueue = initialize();
	DeletedQueue ->currentSize = (1<<min) -1;
	for(i = min-1; i>=0; i--)
	{
		DeletedQueue ->theTrees[i] = DeletedTree;
		DeletedTree = DeletedTree->nextSibling;
		DeletedQueue ->theTrees[i]->nextSibling =NULL;
	}

	H->theTrees[min] = NULL;
	H->currentSize -= DeletedQueue->currentSize+1;
	merge(H, DeletedQueue);
	return minValue;
}

测试截图：

第一部分二项队列拥有B0，B1，B2，B4。进行了两次删除最小值之后，只剩下B0,B2,B4部分了。

总结：

二项队列的实现还是挺费脑子的，当时课本上并没有详细讲解二项队列怎么表示，只贴了一张图，我只能看代码一步步的理解，一步步的画图。才明白过来它的Leftchild和NextSibling代表的意思。我在这里详细解释了一下，希望能帮到阅读我博客的朋友。

第二个难点就是我最后显示出来的图了。比如说测试图第二部分的B4。看起来其中的3,5,4,6不是比根父节点10，7小吗，怎么会处在树的底部呢？当初我也把这一部分当做了bug，然后跟着一步步调试，发现实现没错啊。

然后仔细想了想，我这里画图的方式是把NextSibling当做右孩子来处理的，这样画出来的图接近二叉树（其实可以把NextSibling正确处理，但是我想明白没问题后就没有动力了。。）。图中每个节点上面的孩子代表Leftchild，下面的孩子代表NextSibling，所以3的根节点实际上不是10，而是1。其他几个问题也是同样的，仔细看一看结构就可以明白。