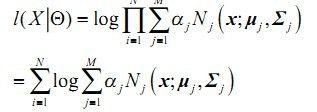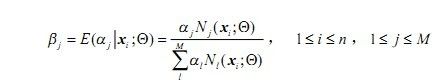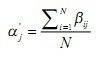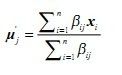Opencv学习笔记（十）高斯混合模型

原创文章，转载请注明：http://blog.csdn.net/crzy_sparrow/article/details/7413019

 

   好吧，我承认这个题目有点噱头，其实本文要讲的一般的高斯混合模型，基于matlab实现，没有涉及到opencv。之所以作为opencv的学习笔记之一是因为之后打算讲下基于高斯混合模型的背景建模（实现目标跟踪），所以把这个也放上来了。

    混合高斯模型的原理说白了就一句话：任意形状的概率分布都可以用多个高斯分布函数去近似。换句话说，高斯混合模型（GMM）可以平滑任意形状的概率分布。其参数求解方法一般使用极大似然估计求解，但使用极大似然估计法往往不能获得完整数据（比如样本已知，但样本类别（属于哪个高斯分布）未知），于是出现了EM（最大期望值）求解方法。

    虽然上面说的简单，但是混合高斯模型和EM求解的理论还是比较复杂的，我把我所找到的我认为能够快速掌握高斯混合模型的资料打包到了附件中，大家可以去下载，了解混合高斯模型以及EM的完整推导过程。

附件下载地址：

http://download.csdn.net/detail/crzy_sparrow/4187994

大致抽取下高斯混合模型的重要概念：

1）任意数据分布可用高斯混合模型（M个单高斯）表示（（1）式）

（1）

其中：

    （2）

   （3）   表示第j个高斯混合模型

2）N个样本集X的log似然函数如下：

     （4）

其中：

参数：，   （5）

下面具体讲讲基于EM迭代的混合高斯模型参数求解算法流程：

1）初始参数由k-means（其实也是一种特殊的高斯混合模型）决定：

function [Priors, Mu, Sigma] = EM_init_kmeans(Data, nbStates)
% Inputs -----------------------------------------------------------------
%   o Data:     D x N array representing N datapoints of D dimensions.
%   o nbStates: Number K of GMM components.
% Outputs ----------------------------------------------------------------
%   o Priors:   1 x K array representing the prior probabilities of the
%               K GMM components.
%   o Mu:       D x K array representing the centers of the K GMM components.
%   o Sigma:    D x D x K array representing the covariance matrices of the 
%               K GMM components.
% Comments ---------------------------------------------------------------
%   o This function uses the 'kmeans' function from the MATLAB Statistics 
%     toolbox. If you are using a version of the 'netlab' toolbox that also
%     uses a function named 'kmeans', please rename the netlab function to
%     'kmeans_netlab.m' to avoid conflicts. 

[nbVar, nbData] = size(Data);

%Use of the 'kmeans' function from the MATLAB Statistics toolbox
[Data_id, Centers] = kmeans(Data', nbStates); 
Mu = Centers';
for i=1:nbStates
  idtmp = find(Data_id==i);
  Priors(i) = length(idtmp);
  Sigma(:,:,i) = cov([Data(:,idtmp) Data(:,idtmp)]');
  %Add a tiny variance to avoid numerical instability
  Sigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(nbVar,1));
end
Priors = Priors ./ sum(Priors);

2）E步（求期望）

求取：

（7）

其实，这里最贴切的式子应该是log似然函数的期望表达式

事实上，3）中参数的求取也是用log似然函数的期望表达式求偏导等于0解得的简化后的式子，而这些式子至于（7）式有关，于是E步可以只求（7）式，以此简化计算，不需要每次都求偏导了。

  %% E-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
  for i=1:nbStates
    %Compute probability p(x|i)
    Pxi(:,i) = gaussPDF(Data, Mu(:,i), Sigma(:,:,i));
  end
  %Compute posterior probability p(i|x)
  Pix_tmp = repmat(Priors,[nbData 1]).*Pxi;
  Pix = Pix_tmp ./ repmat(sum(Pix_tmp,2),[1 nbStates]);
  %Compute cumulated posterior probability
  E = sum(Pix);

function prob = gaussPDF(Data, Mu, Sigma)
% Inputs -----------------------------------------------------------------
%   o Data:  D x N array representing N datapoints of D dimensions.
%   o Mu:    D x K array representing the centers of the K GMM components.
%   o Sigma: D x D x K array representing the covariance matrices of the 
%            K GMM components.
% Outputs ----------------------------------------------------------------
%   o prob:  1 x N array representing the probabilities for the 
%            N datapoints.     

[nbVar,nbData] = size(Data);

Data = Data' - repmat(Mu',nbData,1);
prob = sum((Data*inv(Sigma)).*Data, 2);
prob = exp(-0.5*prob) / sqrt((2*pi)^nbVar * (abs(det(Sigma))+realmin));

3）M步（最大化步骤）

更新权值：

更新均值：

更新方差矩阵：

 %% M-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
  for i=1:nbStates
    %Update the priors
    Priors(i) = E(i) / nbData;
    %Update the centers
    Mu(:,i) = Data*Pix(:,i) / E(i);
    %Update the covariance matrices
    Data_tmp1 = Data - repmat(Mu(:,i),1,nbData);
    Sigma(:,:,i) = (repmat(Pix(:,i)',nbVar, 1) .* Data_tmp1*Data_tmp1') / E(i);
    %% Add a tiny variance to avoid numerical instability
    Sigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(nbVar,1));
  end

4）截止条件

不断迭代EM步骤，更新参数，直到似然函数前后差值小于一个阈值，或者参数前后之间的差（一般选择欧式距离）小于某个阈值，终止迭代，这里选择前者。附上结合EM步骤的代码：

while 1
  %% E-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
  for i=1:nbStates
    %Compute probability p(x|i)
    Pxi(:,i) = gaussPDF(Data, Mu(:,i), Sigma(:,:,i));
  end
  %Compute posterior probability p(i|x)
  Pix_tmp = repmat(Priors,[nbData 1]).*Pxi;
  Pix = Pix_tmp ./ repmat(sum(Pix_tmp,2),[1 nbStates]);
  %Compute cumulated posterior probability
  E = sum(Pix);
  %% M-step %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
  for i=1:nbStates
    %Update the priors
    Priors(i) = E(i) / nbData;
    %Update the centers
    Mu(:,i) = Data*Pix(:,i) / E(i);
    %Update the covariance matrices
    Data_tmp1 = Data - repmat(Mu(:,i),1,nbData);
    Sigma(:,:,i) = (repmat(Pix(:,i)',nbVar, 1) .* Data_tmp1*Data_tmp1') / E(i);
    %% Add a tiny variance to avoid numerical instability
    Sigma(:,:,i) = Sigma(:,:,i) + 1E-5.*diag(ones(nbVar,1));
  end
  %% Stopping criterion %%%%%%%%%%%%%%%%%%%%
  for i=1:nbStates
    %Compute the new probability p(x|i)
    Pxi(:,i) = gaussPDF(Data, Mu(:,i), Sigma(:,:,i));
  end
  %Compute the log likelihood
  F = Pxi*Priors';
  F(find(F<realmin)) = realmin;
  loglik = mean(log(F));
  %Stop the process depending on the increase of the log likelihood 
  if abs((loglik/loglik_old)-1) < loglik_threshold
    break;
  end
  loglik_old = loglik;
  nbStep = nbStep+1;
end

结果测试（第一幅为样本点集，第二幅表示求取的高斯混合模型，第三幅为回归模型）：

忘了说了，传统的GMM和k-means一样，需要给定K值（即:要有几个高斯函数）。