彻底搞懂红黑树（二）
其实关于红黑树，STL源码剖析---红黑树原理详解 已经写得非常好了。但套用新警察故事里的谢霆锋说的一句话：自己查，印象深一点。这里也是一样，在自己写，印象深一点。如果你要看正宗的STL源码剖析---红黑树原理详解，那请你点击这个。这里的是D版的o(╯□╰)o 当然，我也会加一些我自己的理解，因为大神写文章都比较精简，而我这是写给我自己看的，有一点口水话加深点印象。
三 红黑树的插入
红黑树的节点插入默认是节点为红色的。我自己理解是，其实插入红还是黑都可以，但就要看后面的调整是否麻烦。
插入黑点，会增加路径上黑点的数目，一定会破坏性质5
插入红点：
当其父节点为黑色时，不影响平衡，继续保持红黑性质
当其父节点为红色时，可能破坏性质2（根节点是黑色的）、性质4（红色节点的子节点一定是黑色节点），需要进行修正。
因为第一篇文章已经说了，黑节点至少是红节点的两倍，这说明插入红节点OK的概率高很多（因为父节点为黑，插入子节点为红色就不会和性质冲突），这样插入就省事多了，嘿嘿，这也是红黑树为什么战胜AVL树的原因之一，插入效率高啊，节点贴上去就ok了，都不用什么左转右转调整了，多省事啊；再说，如果插入子节点为黑色，o(╯□╰)o了，黑高度变化了，得调整，如果每次都插入黑节点，都得调整，没事闲的蛋疼啊。。。
红黑树插入分一下几种情况：
1、黑父
如下图所示，如果新节点的父结点为黑色结点，那么插入一个红点将不会影响红黑树的平衡，此时插入操作完成。红黑树比AVL树优秀的地方之一在于黑父的情况比较常见，从而使红黑树需要旋转的几率相对AVL树来说会少一些。（大神和我的理解差不多，不过别人的精简很多，我的就是口水话。）
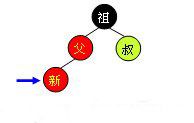
如果新节点的父结点为红色，这时就需要进行一系列操作以保证整棵树红黑性质。如下图所示，由于父结点为红色，此时可以判定，祖父结点必定为黑色。这时需要根据叔父结点的颜色来决定做什么样的操作。青色结点表示颜色未知。由于有可能需要根结点到新点的路径上进行多次旋转操作，而每次进行不平衡判断的起始点（我们可将其视为新点）都不一样。所以我们在此使用一个蓝色箭头指向这个起始点，并称之为判定点。
图一
2.1 红叔当叔父结点为红色时，如下图所示，无需进行旋转操作，只要将父和叔结点变为黑色，将祖父结点变为红色即可。但由于祖父结点的父结点有可能为红色，从而违反红黑树性质。此时必须将祖父结点作为新的判定点继续向上（迭代）进行平衡操作。（注意这里是需要迭代的，有可能会调整到根节点）
图二
需要注意的是，无论“父节点”在“叔节点”的左边还是右边，无论“新节点”是“父节点”的左孩子还是右孩子，它们的操作都是完全一样的（其实这种情况包括4种，只需调整颜色，不需要旋转树形）。
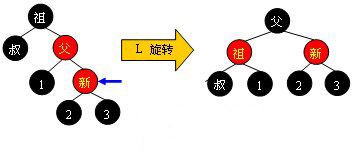
2.2 黑叔
当叔父结点为黑色时，需要进行旋转，以下图示了所有的旋转可能：（case1 和caes 2 都是把左边较大的节点调整到上面去）
Case 1:
图三
Case 2:
图四
其实这里case 2的图示进行了简化，就是case 2 需要L变换成case 1 的情形如图五，然后再进行R旋转，得到最后的结果。
当然，下面的也一样
图五（图中省略了哨兵结点）
Case 4:
有了上面的分析，红黑树的插入就好理解多了，代码也容易读懂。不过不是很喜欢c++的代码，有时间了把linux内核的红黑树源码贴出来。这里还是贴的大神注视的红黑树的插入操作源代码：
stl里的红黑树插入操作源码
// 元素插入操作 insert_unique()
// 插入新值：节点键值不允许重复，若重复则插入无效
// 注意，返回值是个pair，第一个元素是个红黑树迭代器，指向新增节点
// 第二个元素表示插入成功与否
template<class Key , class Value , class KeyOfValue , class Compare , class Alloc>
pair<typename rb_tree<Key , Value , KeyOfValue , Compare , Alloc>::iterator , bool>
rb_tree<Key , Value , KeyOfValue , Compare , Alloc>::insert_unique(const Value &v)
{
rb_tree_node* y = header; // 根节点root的父节点
rb_tree_node* x = root(); // 从根节点开始
bool comp = true;
while(x != 0)
{
y = x;
comp = key_compare(KeyOfValue()(v) , key(x)); // v键值小于目前节点之键值？
x = comp ? left(x) : right(x); // 遇“大”则往左，遇“小于或等于”则往右
}
// 离开while循环之后，y所指即插入点之父节点（此时的它必为叶节点）
iterator j = iterator(y); // 令迭代器j指向插入点之父节点y
if(comp) // 如果离开while循环时comp为真（表示遇“大”，将插入于左侧）
{
if(j == begin()) // 如果插入点之父节点为最左节点
return pair<iterator , bool>(_insert(x , y , z) , true);
else // 否则（插入点之父节点不为最左节点）
--j; // 调整j，回头准备测试
}
if(key_compare(key(j.node) , KeyOfValue()(v) ))
// 新键值不与既有节点之键值重复，于是以下执行安插操作
return pair<iterator , bool>(_insert(x , y , z) , true);
// 以上，x为新值插入点，y为插入点之父节点，v为新值
// 进行至此，表示新值一定与树中键值重复，那么就不应该插入新值
return pair<iterator , bool>(j , false);
}
// 真正地插入执行程序 _insert()
template<class Key , class Value , class KeyOfValue , class Compare , class Alloc>
typename<Key , Value , KeyOfValue , Compare , Alloc>::_insert(base_ptr x_ , base_ptr y_ , const Value &v)
{
// 参数x_ 为新值插入点，参数y_为插入点之父节点，参数v为新值
link_type x = (link_type) x_;
link_type y = (link_type) y_;
link_type z;
// key_compare 是键值大小比较准则。应该会是个function object
if(y == header || x != 0 || key_compare(KeyOfValue()(v) , key(y) ))
{
z = create_node(v); // 产生一个新节点
left(y) = z; // 这使得当y即为header时，leftmost() = z
if(y == header)
{
root() = z;
rightmost() = z;
}
else if(y == leftmost()) // 如果y为最左节点
leftmost() = z; // 维护leftmost()，使它永远指向最左节点
}
else
{
z = create_node(v); // 产生一个新节点
right(y) = z; // 令新节点成为插入点之父节点y的右子节点
if(y == rightmost())
rightmost() = z; // 维护rightmost()，使它永远指向最右节点
}
parent(z) = y; // 设定新节点的父节点
left(z) = 0; // 设定新节点的左子节点
right(z) = 0; // 设定新节点的右子节点
// 新节点的颜色将在_rb_tree_rebalance()设定（并调整）
_rb_tree_rebalance(z , header->parent); // 参数一为新增节点，参数二为根节点root
++node_count; // 节点数累加
return iterator(z); // 返回一个迭代器，指向新增节点
}
// 全局函数
// 重新令树形平衡（改变颜色及旋转树形）
// 参数一为新增节点，参数二为根节点root
inline void _rb_tree_rebalance(_rb_tree_node_base* x , _rb_tree_node_base*& root)
{
x->color = _rb_tree_red; //新节点必为红
while(x != root && x->parent->color == _rb_tree_red) // 父节点为红
{
if(x->parent == x->parent->parent->left) // 父节点为祖父节点之左子节点
{
_rb_tree_node_base* y = x->parent->parent->right; // 令y为伯父节点
if(y && y->color == _rb_tree_red) // 伯父节点存在，且为红
{
x->parent->color = _rb_tree_black; // 更改父节点为黑色
y->color = _rb_tree_black; // 更改伯父节点为黑色
x->parent->parent->color = _rb_tree_red; // 更改祖父节点为红色
x = x->parent->parent;
}
else // 无伯父节点，或伯父节点为黑色
{
if(x == x->parent->right) // 如果新节点为父节点之右子节点
{
x = x->parent;
_rb_tree_rotate_left(x , root); // 第一个参数为左旋点
}
x->parent->color = _rb_tree_black; // 改变颜色
x->parent->parent->color = _rb_tree_red;
_rb_tree_rotate_right(x->parent->parent , root); // 第一个参数为右旋点
}
}
else // 父节点为祖父节点之右子节点
{
_rb_tree_node_base* y = x->parent->parent->left; // 令y为伯父节点
if(y && y->color == _rb_tree_red) // 有伯父节点，且为红
{
x->parent->color = _rb_tree_black; // 更改父节点为黑色
y->color = _rb_tree_black; // 更改伯父节点为黑色
x->parent->parent->color = _rb_tree_red; // 更改祖父节点为红色
x = x->parent->parent; // 准备继续往上层检查
}
else // 无伯父节点，或伯父节点为黑色
{
if(x == x->parent->left) // 如果新节点为父节点之左子节点
{
x = x->parent;
_rb_tree_rotate_right(x , root); // 第一个参数为右旋点
}
x->parent->color = _rb_tree_black; // 改变颜色
x->parent->parent->color = _rb_tree_red;
_rb_tree_rotate_left(x->parent->parent , root); // 第一个参数为左旋点
}
}
}//while
root->color = _rb_tree_black; // 根节点永远为黑色
}
// 左旋函数
inline void _rb_tree_rotate_left(_rb_tree_node_base* x , _rb_tree_node_base*& root)
{
// x 为旋转点
_rb_tree_node_base* y = x->right; // 令y为旋转点的右子节点
x->right = y->left;
if(y->left != 0)
y->left->parent = x; // 别忘了回马枪设定父节点
y->parent = x->parent;
// 令y完全顶替x的地位（必须将x对其父节点的关系完全接收过来）
if(x == root) // x为根节点
root = y;
else if(x == x->parent->left) // x为其父节点的左子节点
x->parent->left = y;
else // x为其父节点的右子节点
x->parent->right = y;
y->left = x;
x->parent = y;
}
// 右旋函数
inline void _rb_tree_rotate_right(_rb_tree_node_base* x , _rb_tree_node_base*& root)
{
// x 为旋转点
_rb_tree_node_base* y = x->left; // 令y为旋转点的左子节点
x->left = y->right;
if(y->right != 0)
y->right->parent = x; // 别忘了回马枪设定父节点
y->parent = x->parent;
// 令y完全顶替x的地位（必须将x对其父节点的关系完全接收过来）
if(x == root)
root = y;
else if(x == x->parent->right) // x为其父节点的右子节点
x->parent->right = y;
else // x为其父节点的左子节点
x->parent->left = y;
y->right = x;
x->parent = y;
}
linux 源码里的红黑树插入
自认为好读多了 O(∩_∩)O~
/**
* node是新插入的结点，有着默认的红色。
* 本函数检查是否有违背红黑树性质的地方，并进行纠正。
*/
void rb_insert_color(rb_node *node, rb_root *root) {
rb_node *parent, *gp;
/**
* 如果有父节点且父节点是红色，进行树的调整以保证树的性质。
*/
while ((parent = rb_parent(node)) && rb_is_red(parent)) {
gp = rb_parent(parent);
if (parent == gp->left) {
/**
* 父节点是祖父节点左子的情况。
* "else"中的情况左右相反，这里只注释"if"里的代码。
*/
register rb_node *uncle = gp->right;
if (uncle && rb_is_red(uncle)) { //对应图一
/**
* 如果有红叔，则将红叔与红父均涂黑，并将祖父节点涂红。
*/
rb_set_black(parent);
rb_set_black(uncle);
rb_set_red(gp);
/**
* 现在简单路径中黑节点个数仍然平衡，但祖父变成了红色，
* 我们不确定有没有造成父子均红的情况，所以需要对祖父节点进行下一轮修复。
*/
node = gp; //这里要递归fix
continue;
}
/**
* 现在是叔节点为空或为黑的情况。
*/
if (node == parent->right) {
/**
* 如果新节点是父节点的右子，对父节点进行左旋。
* 旋转后树仍然平衡，但新节点占了原父节点的位子。
* 这两个节点交换角色后，新的父节点是红的，其左子也是红的。
*/
_rb_rotate_left(parent, root); //对应图四-》图五
register rb_node *tmp = node;
node = parent;
parent = tmp;
}
/**
* 此时父红左子红，树平衡但有连续红节点。
*
* 父涂黑，祖父涂红，再对祖父右旋，树即调整到合法状态。
*/
rb_set_black(parent); //对应图三
rb_set_red(gp);
_rb_rotate_right(gp, root);
return;
} else {
register rb_node *uncle = gp->left;
if (uncle && rb_is_red(uncle)) {
rb_set_black(parent);
rb_set_black(uncle);
rb_set_red(gp);
node = gp;
continue;
}
if (node == parent->left) {
_rb_rotate_right(parent, root);
register rb_node *tmp = node;
node = parent;
parent = tmp;
}
rb_set_black(parent);
rb_set_red(gp);
_rb_rotate_left(gp, root);
return;
}
}
/**
* 若无父节点，只需将node涂黑；
* 若父节点为黑，插入红节点不影响树的性质。
* 循环体后直接将node涂黑，可以同时保证以上两点。
*/
rb_set_black(root->node);
}