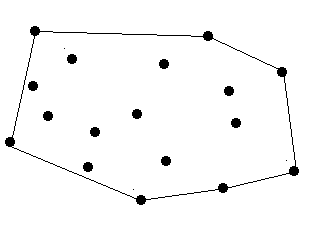
(hdu step 7.1.4)Surround the Trees(求凸包的周长——计算将所有点都包围起来的最小凸多边形的周长)
题意:
题目分析:
求凸包的周长。这道题和拿到Wall的题目是差不多。需要注意一下的是,这道题中的结点的个数可能<=2,这个需要单独处理一下。
代码如下:
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const double epsi = 1e-8;
const double pi = acos(-1.0);
const int maxn = 101;
struct PPoint{//结构体尽量不要定义成Point这种,容易和C/C++本身中的变量同名
double x;
double y;
PPoint(double _x = 0,double _y = 0):x(_x),y(_y){
}
PPoint operator - (const PPoint& op2) const{
return PPoint(x - op2.x,y - op2.y);
}
double operator^(const PPoint &op2)const{
return x*op2.y - y*op2.x;
}
};
inline int sign(const double &x){
if(x > epsi){
return 1;
}
if(x < -epsi){
return -1;
}
return 0;
}
inline double sqr(const double &x){
return x*x;
}
inline double mul(const PPoint& p0,const PPoint& p1,const PPoint& p2){
return (p1 - p0)^(p2 - p0);
}
inline double dis2(const PPoint &p0,const PPoint &p1){
return sqr(p0.x - p1.x) + sqr(p0.y - p1.y);
}
inline double dis(const PPoint& p0,const PPoint& p1){
return sqrt(dis2(p0,p1));
}
int n;
PPoint p[maxn];
PPoint convex_hull_p0;
inline bool convex_hull_cmp(const PPoint& a,const PPoint& b){
return sign(mul(convex_hull_p0,a,b)>0)|| (sign(mul(convex_hull_p0,a,b)) == 0 && dis2(convex_hull_p0,a) < dis2(convex_hull_p0,b));
}
int convex_hull(PPoint* a,int n,PPoint* b){
int i;
for(i = 1 ; i < n ; ++i){
if(sign(a[i].x - a[0].x) < 0 || (sign(a[i].x - a[0].x) == 0 && sign(a[i].y - a[0].y) < 0)){
swap(a[i],a[0]);
}
}
convex_hull_p0 = a[0];//这两行代码不要顺序调换了..否则会WA
sort(a,a+n,convex_hull_cmp);
b[0] = a[0];
b[1] = a[1];
int newn = 2;
for(i = 2 ; i < n ; ++i){
while(newn > 1 && sign(mul(b[newn-1],b[newn-2],a[i])) >= 0){
newn--;
}
b[newn++] = a[i];
}
return newn;
}
int main(){
while(scanf("%d",&n)!=EOF,n){
int i;
for(i = 0 ; i < n ; ++i){
scanf("%lf %lf",&p[i].x,&p[i].y);
}
/**
* 一定要注意的是,这道题中可能存在结点数 <= 2的情况.
* 而graham计算凸包的算法只适用于结点数>=3的情况.
* 所以需要对节点数<=2的情况做一下处理...
*/
if(n < 2){//如果节点数<2
printf("0.00\n");//则直接输出0.00
continue;//进行下一次循环
}
if(n == 2){//如果结点数 == 2
printf("%.2lf\n",dis(p[0],p[1]));//则直接计算p[0]和p[1]的距离即可..
continue;//进行下一次循环
}
n = convex_hull(p,n,p);
p[n] = p[0];//首尾相接.将最后一个点指向起点
double ans = 0;
for(i = 0 ; i < n ; ++i){//计算凸包的周长
ans += dis(p[i],p[i+1]);
}
printf("%.2lf\n",ans);
}
return 0;
}