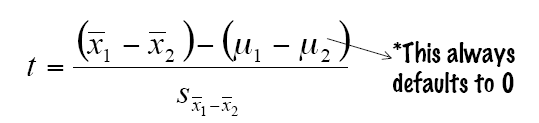数据分析之可重复与独立样本的T-Test分析
数据分析之独立样本的T-Test分析
比较两个独立样本数据之间是否有显著性差异,将实验数据与标准数据对比,查看
实验结果是否符合预期。T-Test在生物数据分析,实验数据效果验证中很常见的数
据处理方法。http://www.statisticslectures.com/tables/ttable/ - T-table查找表
独立样本T-test条件:
1. 每个样本相互独立没有影响
2. 样本大致符合正态分布曲线
3. 具有同方差异性
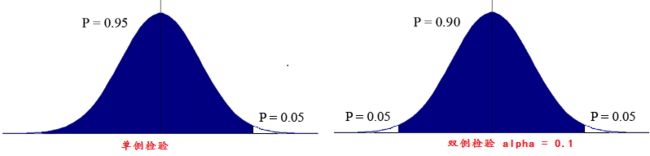
单侧检验(one-tail Test)与双侧检验(Two-Tail Test)
基本步骤:
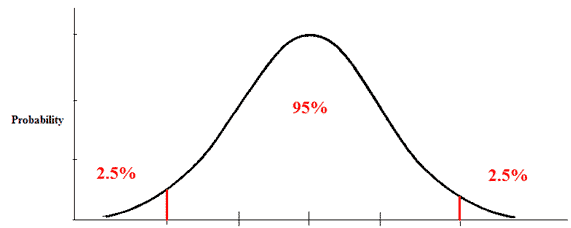
1.双侧检验, 条件声明 alpha值设置为0.05
根据t-table, alpha = 0.05, df = 38时, 对于t-table的值为2.0244
2. 计算自由度(Degree of Freedom)
Df = (样本1的总数 + 样本2的总数)- 2
3. 声明决策规则
如果计算出来的结果t-value的结果大于2.0244或者小于-2.0244则拒绝
4. 计算T-test统计值
5. 得出结论
如果计算结果在双侧区间之内,说明两组样本之间没有显著差异。
可重复样本的T-Test计算
同样一组数据在不同的条件下得到结果进行比对,发现是否有显著性差异,最常见
的对一个人在饮酒与不饮酒条件下驾驶车辆测试,很容易得出酒精对驾驶员有显著
影响
算法实现:
对独立样本的T-Test计算最重要的是计算各自的方差与自由度df1与df2
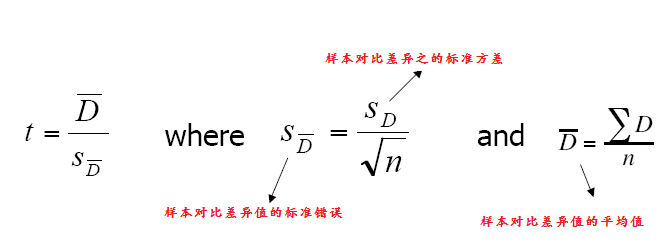
对可重复样本的对比t-test计算
程序实现:
package com.gloomyfish.data.mining.analysis;
public class TTestAnalysisAlg {
private double alpahValue = 0.05; // default
private boolean dependency = false; // default
public TTestAnalysisAlg() {
System.out.println("t-test algorithm");
}
public double getAlpahValue() {
return alpahValue;
}
public void setAlpahValue(double alpahValue) {
this.alpahValue = alpahValue;
}
public boolean isDependency() {
return dependency;
}
public void setDependency(boolean dependency) {
this.dependency = dependency;
}
public double analysis(double[] data1, double[] data2) {
double tValue = 0;
if (dependency) {
// Repeated Measures T-test.
// Uses the same sample of subjects measured on two different
// occasions
double diffSum = 0.0;
double diffMean = 0.0;
int size = Math.min(data1.length, data2.length);
double[] diff = new double[size];
for(int i=0; i<size; i++)
{
diff[i] = data2[i] -data1[i];
diffSum += data2[i] -data1[i];
}
diffMean = diffSum / size;
diffSum = 0.0;
for(int i=0; i<size; i++)
{
diffSum += Math.pow((diff[i] -diffMean), 2);
}
double diffSD = Math.sqrt(diffSum / (size - 1.0));
double diffSE = diffSD / Math.sqrt(size);
tValue = diffMean / diffSE;
} else {
double means1 = 0;
double means2 = 0;
double sum1 = 0;
double sum2 = 0;
// calcuate means
for (int i = 0; i < data1.length; i++) {
sum1 += data1[i];
}
for (int i = 0; i < data2.length; i++) {
sum2 += data2[i];
}
means1 = sum1 / data1.length;
means2 = sum2 / data2.length;
// calculate SD (Standard Deviation)
sum1 = 0.0;
sum2 = 0.0;
for (int i = 0; i < data1.length; i++) {
sum1 += Math.pow((means1 - data1[i]), 2);
}
for (int i = 0; i < data2.length; i++) {
sum2 += Math.pow((means2 - data2[i]), 2);
}
double sd1 = Math.sqrt(sum1 / (data1.length - 1.0));
double sd2 = Math.sqrt(sum2 / (data2.length - 1.0));
// calculate SE (Standard Error)
double se1 = sd1 / Math.sqrt(data1.length);
double se2 = sd2 / Math.sqrt(data2.length);
System.out.println("Data Sample one - > Means :" + means1
+ " SD : " + sd1 + " SE : " + se1);
System.out.println("Data Sample two - > Means :" + means2
+ " SD : " + sd2 + " SE : " + se2);
// degree of freedom
double df1 = data1.length - 1;
double df2 = data2.length - 1;
// Calculate the estimated standard error of the difference
double spooled2 = (sd1 * sd1 * df1 + sd2 * sd2 * df2) / (df1 + df2);
double Sm12 = Math.sqrt((spooled2 / df1 + spooled2 / df2));
tValue = (means1 - means2) / Sm12;
}
System.out.println("t-test value : " + tValue);
return tValue;
}
public static void main(String[] args) {
int size = 10;
System.out.println(Math.sqrt(size));
}
}
测试程序:
package com.gloomyfish.dataming.study;
import com.gloomyfish.data.mining.analysis.TTestAnalysisAlg;
public class TTestDemo {
public static double[] data1 = new double[]{
35, 40, 12, 15, 21, 14, 46, 10, 28, 48, 16, 30, 32, 48, 31, 22, 12, 39, 19, 25
};
public static double[] data2 = new double[]{
2, 27, 38, 31, 1, 19, 1, 34, 3, 1, 2, 3, 2, 1, 2, 1, 3, 29, 37, 2
};
public static void main(String[] args)
{
TTestAnalysisAlg tTest = new TTestAnalysisAlg();
tTest.analysis(data1, data2);
tTest.setDependency(true);
double[] d1 = new double[]{2, 0, 4, 2, 3};
double[] d2 = new double[]{8, 4, 11, 5, 8};
// The critical value for a one-tailed t-test with
// df=4 and α=.05 is 2.132
double t = tTest.analysis(d1, d2);
if(t > 2.132 || t < -2.132)
{
System.err.println("Very Bad!!!!");
}
}
}