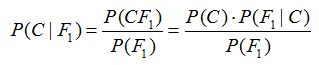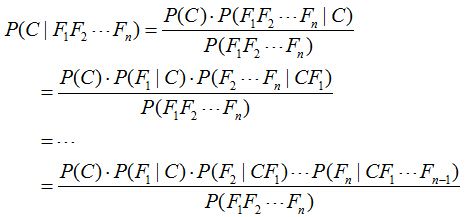用Python开始机器学习（6：朴素贝叶斯分类器）

朴素贝叶斯分类器是一个以贝叶斯定理为基础，广泛应用于情感分类领域的优美分类器。本文我们尝试使用该分类器来解决上一篇文章中影评态度分类。

1、贝叶斯定理

假设对于某个数据集，随机变量C表示样本为C类的概率，F1表示测试样本某特征出现的概率，套用基本贝叶斯公式，则如下所示：

上式表示对于某个样本，特征F1出现时，该样本被分为C类的条件概率。那么如何用上式来对测试样本分类呢？

举例来说，有个测试样本，其特征F1出现了（F1=1），那么就计算P(C=0|F1=1)和P(C=1|F1=1)的概率值。前者大，则该样本被认为是0类；后者大，则分为1类。

对该公示，有几个概念需要熟知：

先验概率（Prior）。P(C)是C的先验概率，可以从已有的训练集中计算分为C类的样本占所有样本的比重得出。

证据（Evidence）。即上式P(F1)，表示对于某测试样本，特征F1出现的概率。同样可以从训练集中F1特征对应样本所占总样本的比例得出。

似然（likelihood）。即上式P(F1|C)，表示如果知道一个样本分为C类，那么他的特征为F1的概率是多少。

对于多个特征而言，贝叶斯公式可以扩展如下：

分子中存在一大串似然值。当特征很多的时候，这些似然值的计算是极其痛苦的。现在该怎么办？

2、朴素的概念

为了简化计算，朴素贝叶斯算法做了一假设：“朴素的认为各个特征相互独立”。这么一来，上式的分子就简化成了：

P(C)*P(F1|C)*P(F2|C)...P(Fn|C)。

这样简化过后，计算起来就方便多了。

这个假设是认为各个特征之间是独立的，看上去确实是个很不科学的假设。因为很多情况下，各个特征之间是紧密联系的。然而在朴素贝叶斯的大量应用实践实际表明其工作的相当好。

其次，由于朴素贝叶斯的工作原理是计算P(C=0|F1...Fn)和P(C=1|F1...Fn)，并取最大值的那个作为其分类。而二者的分母是一模一样的。因此，我们又可以省略分母计算，从而进一步简化计算过程。

另外，贝叶斯公式推导能够成立有个重要前期，就是各个证据（evidence）不能为0。也即对于任意特征Fx，P(Fx)不能为0。而显示某些特征未出现在测试集中的情况是可以发生的。因此实现上通常要做一些小的处理，例如把所有计数进行+1（加法平滑(additive smoothing，又叫拉普拉斯平滑(Laplace smothing)）。而如果通过增加一个大于0的可调参数alpha进行平滑，就叫Lidstone平滑。

例如，在所有6个分为C=1的影评样本中，某个特征F1=1不存在，则P(F1=1|C=1)  = 0/6，P(F1=0|C=1)  = 6/6。

经过加法平滑后，P(F1=1|C=1)  = (0+1)/(6+2)=1/8，P(F1=0|C=1)  = (6+1)/(6+2)=7/8。

注意分母的+2，这种特殊处理使得2个互斥事件的概率和恒为1。

最后，我们知道，当特征很多的时候，大量小数值的小数乘法会有溢出风险。因此，通常的实现都是将其转换为log：

log[P(C)*P(F1|C)*P(F2|C)...P(Fn|C)] = log[P(C)]+log[P(F1|C)] + ... +log[P(Fn|C)]

将乘法转换为加法，就彻底避免了乘法溢出风险。

为确保掌握朴素贝叶斯分类原理，我们先使用上一篇文章最后的文本向量化结果做一个例子：

上述训练集中共8个样本，其中C=0的3个，C=1的5个。现在，假设给你一个测试样本"nb movie"，使用加一平滑进行朴素贝叶斯的分类过程如下：

 P(C=0)=3/8， P(C=1)=5/8。特征F1="nb", F2="movie"。

分为C=0的概率：P(F1=1, F2=1|C=0) = P(C=0)*P(F1=1|C=0)*P(F2=1|C=0) = 3/8 * (0+1)/(3+2) * (1+1)/(3+2) = 3/8 * 1/5 * 2/5 = 0.03。

分为C=1的概率：P(F1=1, F2=1|C=1) = P(C=1)*P(F1=1|C=1)*P(F2=1|C=1) = 5/8 * (3+1)/(5+2) * (3+1)/(5+2) = 5/8 * 4/7 * 4/7 = 0.20。

分为C=1的概率更大。因此将该样本分为C=1类。

（注意：实际计算中还要考虑上表中各个值的TF-IDF，具体计算方式取决于使用哪一类贝叶斯分类器。分类器种类见本文最后说明）

3、测试数据

本文使用上一篇博客中提到的康奈尔大学网站的2M影评数据集。下载地址http://download.csdn.net/detail/lsldd/9346233

每一个特征值就是一个单词的TF-IDF。当然，也可以简单的使用单词出现的次数。

使用这个比较大的数据集，可以做一点点数据预处理的优化来避免每次都去硬盘读取文件。第一次运行时，把读入的数据保存起来，以后就不用每次再去读取了。

#保存
movie_reviews = load_files('endata')
sp.save('movie_data.npy', movie_data)
sp.save('movie_target.npy', movie_target)

#读取
movie_data   = sp.load('movie_data.npy')
movie_target = sp.load('movie_target.npy')

4、代码与分析

Python代码如下：

# -*- coding: utf-8 -*-
from matplotlib import pyplot
import scipy as sp
import numpy as np
from sklearn.datasets import load_files
from sklearn.cross_validation import train_test_split
from sklearn.feature_extraction.text import  CountVectorizer
from sklearn.feature_extraction.text import  TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import classification_report

'''
movie_reviews = load_files('data')
#保存
sp.save('movie_data.npy', movie_reviews.data)
sp.save('movie_target.npy', movie_reviews.target)
'''

#读取
movie_data   = sp.load('movie_data.npy')
movie_target = sp.load('movie_target.npy')
x = movie_data
y = movie_target

#BOOL型特征下的向量空间模型，注意，测试样本调用的是transform接口
count_vec = TfidfVectorizer(binary = False, decode_error = 'ignore',\
                            stop_words = 'english')


#加载数据集，切分数据集80%训练，20%测试
x_train, x_test, y_train, y_test\
    = train_test_split(movie_data, movie_target, test_size = 0.2)
x_train = count_vec.fit_transform(x_train)
x_test  = count_vec.transform(x_test)


#调用MultinomialNB分类器
clf = MultinomialNB().fit(x_train, y_train)
doc_class_predicted = clf.predict(x_test)
    
#print(doc_class_predicted)
#print(y)
print(np.mean(doc_class_predicted == y_test))

#准确率与召回率
precision, recall, thresholds = precision_recall_curve(y_test, clf.predict(x_test))
answer = clf.predict_proba(x_test)[:,1]
report = answer > 0.5
print(classification_report(y_test, report, target_names = ['neg', 'pos']))

输出结果如下所示：

0.821428571429
             precision    recall  f1-score   support
        neg       0.78      0.87      0.83       135
        pos       0.87      0.77      0.82       145
avg / total     0.83      0.82      0.82       280
如果进行多次交叉检验，可以发现朴素贝叶斯分类器在这个数据集上能够达到80%以上的准确率。如果你亲自测试一下，会发现KNN分类器在该数据集上只能达到60%的准确率，相信你对朴素贝叶斯分类器应该能够刮目相看了。而且要知道，情感分类这种带有主观色彩的分类准则，连人类都无法达到100%准确。

要注意的是，我们选用的朴素贝叶斯分类器类别：MultinomialNB，这个分类器以出现次数作为特征值，我们使用的TF-IDF也能符合这类分布。

其他的朴素贝叶斯分类器如GaussianNB适用于高斯分布（正态分布）的特征，而BernoulliNB适用于伯努利分布（二值分布）的特征。