A*寻路算法与它的速度

如果你是一个游戏开发者，或者开发过一些关于人工智能的游戏，你一定知道A*算法，如果没有接触过此类的东东，那么看了这一篇文章，你会对A*算法从不知道变得了解，从了解变得理解。
我不是一个纯粹的游戏开发者，我只是因为喜欢而研究，因为兴趣而开发，从一些很小的游戏开始，直到接触到了寻路等人工智能，才开始查找一些关于寻路方面的文章，从而知道了A*算法，因为对于初期了解的我这个算法比较复杂，开始只是copy而已，现在我们一起来精密的研究一下A*算法，以及提高它的速度的方法。

一，A*算法原理

我看过Panic翻译的国外高手Patrick Lester的一篇关于A*算法初探的文章，现在我就根据回忆，来慢慢认识A*算法的原理。
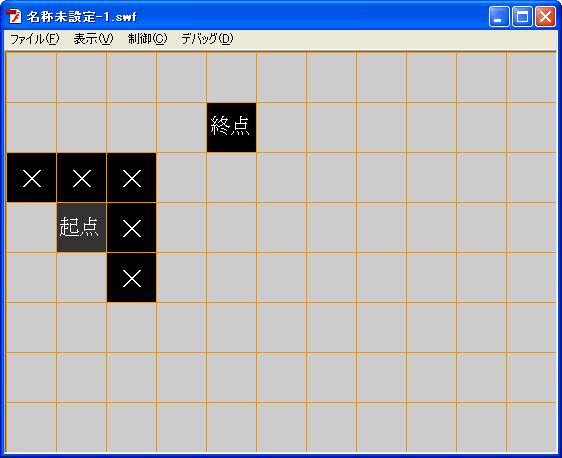
我们先来看一张图

图中从起点到终点，需要绕过一些遮挡，也许我们看的比较简单，但是实际上，交给电脑来实现却要经过一番周折，电脑如何知道哪里有遮挡物，又是如何找到从起点到终点的最短路径的呢？
了解这些，我们首先要知道一个公式：
F = G + H
其中，F 是从起点经过该点到终点的总路程，G 为起点到该点的“已走路程”，H 为该点到终点的“预计路程”。
A*算法，要从起点开始，按照它的算法，逐步查找，直到找到终点。
初期，地图上的节点都是未开启也未关闭的初始状态，我们每检测一个节点，就要开启一些节点，检测完之后，要把检测完的节点，就要把它关闭。
我们需要一个开启列表和关闭列表，用来储存已经被开启的节点和被关闭的节点。
这些就让我们在实际过程中来深入了解吧。
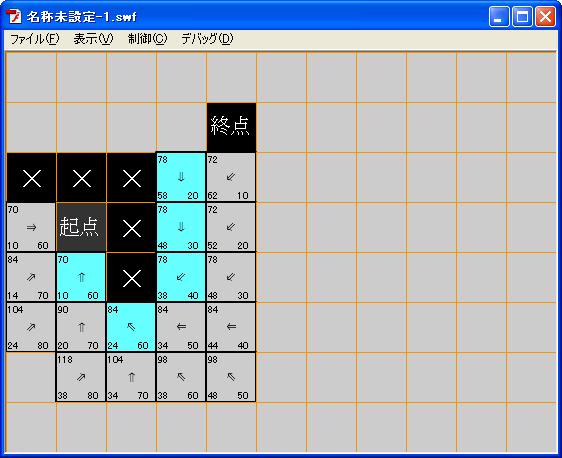
看下面的图

首先，我们来从起点出发，开启它周围的所有点，因为遮挡是无法通过的，我们不去管它，这样，被我们开启的节点，就是图中的三个节点，它们的父节点就是起点，所以图中的箭头指向起点，计算相应的FGH值，如图所视，检测完毕，将起点放入关闭列表。
这个时候，我们从被开启的所有节点中查找F值最小的节点，做为下一次检测的节点，然后开启它周围的点。
这时候起点左方和下方的F值都是70，我们根据自己的喜好选择任意一个，这里先选择下方的节点进行检测。
如下图

首先把未被开启的剩下的节点的父节点指向检测点。
已经开启的点，我们不去开启第二遍，但是我们计算一下从检测点到达它们的新的G值是否更小，如果更小则代表目前的路径是最优的路径，那么把这个节点的父节点改为目前的检测点，并重新计算这个点的FGH的值，全部检测完毕之后，关闭检测点，然后开始寻找下一个节点，如此循环，直到找到终点。
然后从终点开始，按照每个节点的父节点，倒着画出路径，如下图

 

 

这个就是A*算法的原理，说难倒是不难，但是对于初步接触的人来说有点费劲而已。

 

二，A*算法的速度

前面，我们了解了A*算法的原理，发现，在每次查找最小节点的时候，我们需要在开启列表中查找F值最小的节点，研究A*的速度，这里就是关键，如何更快的找出这个最小节点呢？

1，普通查找算法

我们先来看看，最简单的做法，就是每次都把开启列表中所有节点检测一遍，从而找到最小节点

private function getMin():uint { var len:uint = _open.length; var min:Object = new Object(); min.value_f = 100000; min.i = 0; for (var i:uint = 0; i<len; i++) { if (min.value_f>_open[i].value_f) { min.value_f = _open[i].value_f; min.i = i; } } return min.i; }

这里我用了一张很简单的地图来验证此方法
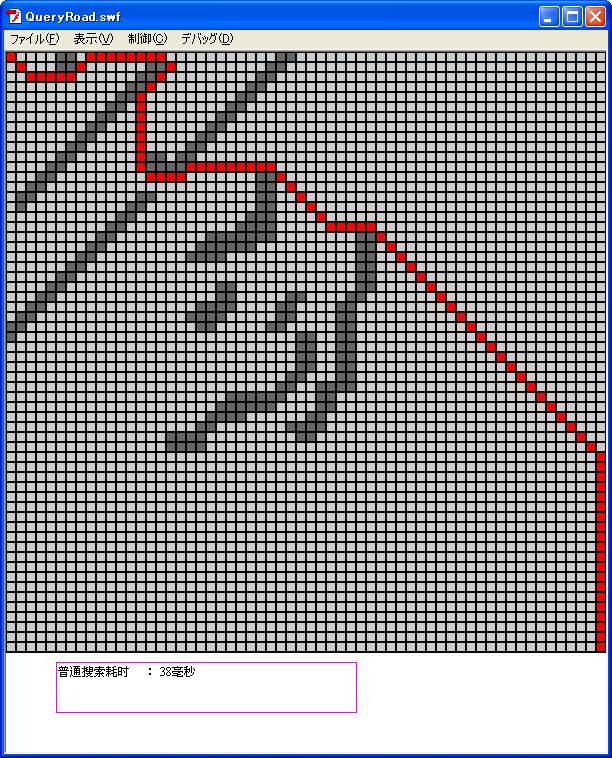
运行结果如图

我们看到，耗时38毫秒，其实这个数字是不准确的，我们权且当作参考

2，排序查找算法

顾名思义，这个算法就是，始终维持开启列表的排序，从小到大，或者从大到小，这样当我们查找最小值时，只需要把第一个节点取出来就行了
维持列表的排序，方法是在太多了，我的方法也许很笨，勉强参考一下吧，我们每次排序的同时，顺便计算列表中的平均值，这样插入新节点的时候，根据这个平均值来判断从前面开始判断还是从后面开始判断

//加入开放列表 private function setOpen(newNode:Object):void { newNode.open = true; var __len:int = _open.length; if (__len==0) { _open.push(newNode); _aveOpen = newNode.value_f; }else { //和F平均值做比较，决定从前面或者后面开始判断 if (newNode.value_f<=_aveOpen) { for (var i:int=0; i<__len; i++) { //找到比F值小的值，就插在此值之前 if (newNode.value_f<=_open[i].value_f) { _open.splice(i, 0, newNode); break; } } } else { for (var j:int=__len; j>0; j--) { //找到比F值大的值，就插在此值之前 if (newNode.value_f>=_open[(j-1)].value_f) { _open.splice(j, 0, newNode); break; } } } //计算开放列表中F平均值 _aveOpen += (newNode.value_f-_aveOpen)/_open.length; } } //取开放列表里的最小值 private function getOpen():Object { var __next:Object = _open.splice(0,1)[0]; //计算开放列表中F平均值 _aveOpen += (_aveOpen-__next.value_f)/_open.length; return __next; }

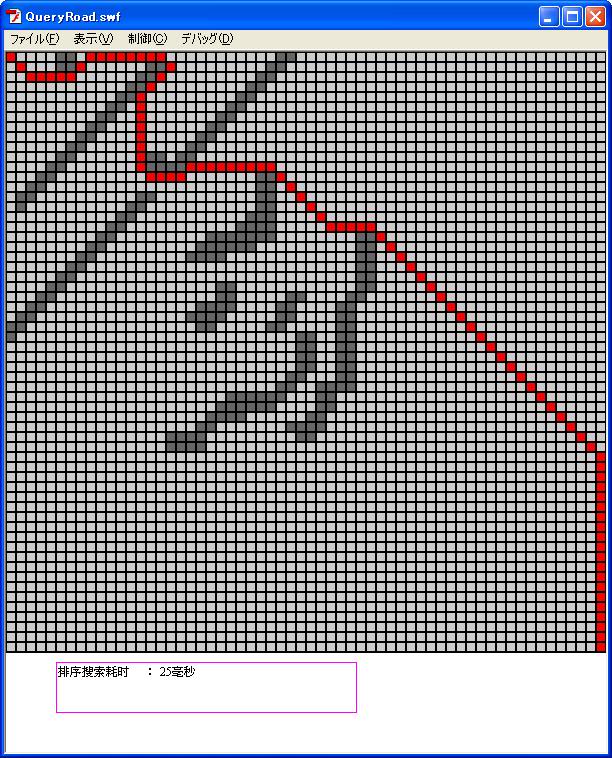
运行结果如图

我们看到，耗时25毫秒，这个数字虽然不准确的，但是与普通查找算法相比较，速度确实是提高了

3，二叉树查找算法
(参考了火夜风舞的C++新霖花园中的文章)
这个算法可以说是A*算法的黄金搭档，也是被称为苛求速度的binary heap”的方法
就是根据二叉树原理，来维持开启列表的“排序”，这里说的排序只是遵循二叉树的原理的排序而已，即父节点永远比子节点小,就像下面这样
   1
|    |
5    9
|   |  |
7  12 10
二叉树每个节点的父节点下标 = n / 2;(小数去掉)
二叉树每个节点的左子节点下标 = n * 2;右子节点下标 = n * 2 +1
注意，这里的下标和它的值是两个概念

//加入开放列表 private function setOpen(newNode:Object,newFlg:Boolean = false):void { var new_index:int; if(newFlg){ newNode.open = true; var new_f:int = newNode.value_f; _open.push(newNode); new_index = _open.length - 1; }else{ new_index = newNode.index; } while(true){ //找到父节点 var f_note_index:int = new_index/2; if(f_note_index > 0){ //如果父节点的F值较大，则与父节点交换 if(_open[new_index].value_f < _open[f_note_index].value_f){ var obj_note:Object = _open[f_note_index]; _open[f_note_index] = _open[new_index]; _open[new_index] = obj_note; _open[f_note_index].index = f_note_index; _open[new_index].index = new_index; new_index = f_note_index; }else{ break; } }else{ break; } } } //取开放列表里的最小值 private function getOpen():Object { if(_open.length <= 1){ return null; } var change_note:Object; //将第一个节点，即F值最小的节点取出，最后返回 var obj_note:Object = _open[1]; _open[1] = _open[_open.length - 1]; _open.pop(); _open[1].index = 1; var this_index:int = 1; while(true){ var left_index:int = this_index * 2; var right_index:int = this_index * 2 + 1; if(left_index >= _open.length){ break; }else if(left_index == _open.length - 1){ //当二叉树只存在左节点时，比较左节点和父节点的F值，若父节点较大，则交换 if(_open[this_index].value_f > _open[left_index].value_f){ change_note = _open[left_index]; _open[left_index] = _open[this_index]; _open[this_index] = change_note; _open[left_index].index = left_index; _open[this_index].index = this_index; this_index = left_index; }else{ break; } }else if(right_index < _open.length){ //找到左节点和右节点中的较小者 if(_open[left_index].value_f <= _open[right_index].value_f){ //比较左节点和父节点的F值，若父节点较大，则交换 if(_open[this_index].value_f > _open[left_index].value_f){ change_note = _open[left_index]; _open[left_index] = _open[this_index]; _open[this_index] = change_note; _open[left_index].index = left_index; _open[this_index].index = this_index; this_index = left_index; }else{ break; } }else{ //比较右节点和父节点的F值，若父节点较大，则交换 if(_open[this_index].value_f > _open[right_index].value_f){ change_note = _open[right_index]; _open[right_index] = _open[this_index]; _open[this_index] = change_note; _open[right_index].index = right_index; _open[this_index].index = this_index; this_index = right_index; }else{ break; } } } } return obj_note; }

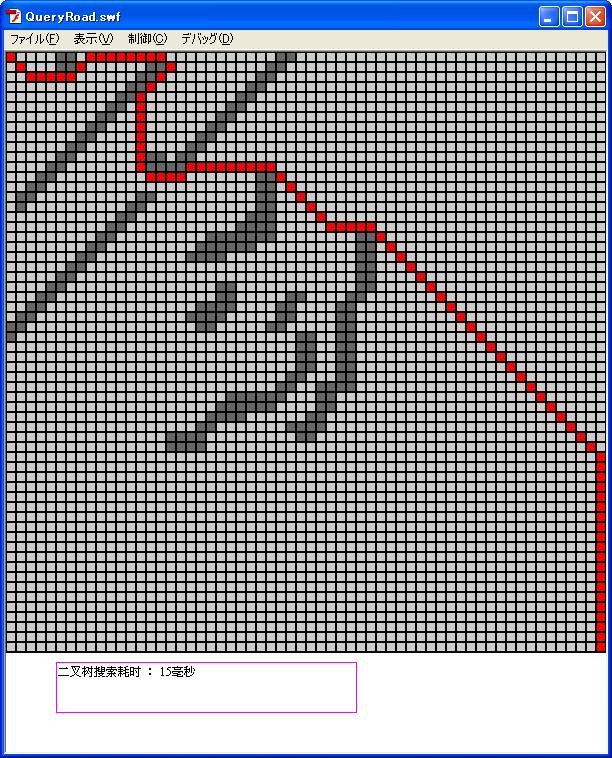
运行结果如图

我们看到，耗时15毫秒，速度是这三个方法里最快的，但是因为这个数字是不够准确的，实际上，用二叉树查找法，会让A*算法的速度提高几倍到10几倍，在一些足够复杂的地图里，这个速度是成指数成长的。

4，总结
得出结论，用了A*算法，就要配套的用它的黄金搭档，二叉树，它可以让你的游戏由完美走向更完美。