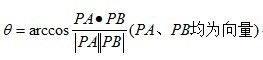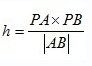POJ1584-A Round Peg in a Ground Hole

 

转载请注明出处：優YoU  http://user.qzone.qq.com/289065406/blog/1309142308

 

大致题意：

按照顺时针或逆时针方向输入一个n边形的顶点坐标集，先判断这个n边形是否为凸包。

再给定一个圆形（圆心坐标和半径），判断这个圆是否完全在n变形内部。

 

解题思路：

题意已经很直白了。。就是那个思路。。。

注意输入完顶点集后，要封闭多边形，方便后面枚举边。

封闭方法：

定义点集数组Vectex[1~n]记录n个顶点，再令Vectex[0]=Vectex[n]，Vectex[n+1]=Vectex[1]

 

1、判断凸包：

   由于点集已经按某个时针方向有序，因此可以先定义一个方向系数direction=0

   两两枚举n边形的边，用叉积判断这两条边的转向（右螺旋或左螺旋），由于存在散点共线的情况，因此当且仅当叉积的值temp第一次不为0时，direction=temp，direction的值此后不再改变。（direction>0 则为右螺旋逆时针，direction<0则为左螺旋顺时针）

   此后继续枚举剩下的边，只要判断direction*temp>=0即可，当存在一个direction*temp<0的边，说明这是凹多边形，就不是凸包了。

2、判断圆心与多边形的关系：

   用环顾法：

   设圆心为P，逐条枚举n边形的边AB，利用

 

   计算PA和PB的夹角，最后求和得到的就是环顾角。

（1）       圆心在多边形内部时，环顾角=±360

（2）       圆心在多边形外部时，环顾角=0

（3）       圆心在多边形边上时（不包括顶点），环顾角=±180

（4）       圆心在多边形顶点时，环顾角为(0,360)之间的任意角，其实就是圆心所在的顶点的两条邻接边的夹角。

3、当圆心在圆内时，判断圆与多边形的关系

   设圆心为P，逐条枚举n边形的边AB，利用得到△PAB的面积，

再根据公式S=0.5*|AB|*h，可以得到 

 枚举所有h与圆的半径R比对，只要所有的边都有R-h>=0，则说明圆在多边形内

 

Source修正：

把原题的“Mid-Atlantic 2003”修正为以下黑斜体内容，可用于找到本题的测试数据

谷歌搜索：

Index of /archive/2003/problems/MidAtlantic-2003

http://midatl.fireduck.com/archive/2003/problems/

 

 

//Memory Time
//268K    0MS 

#include<iostream>
#include<cmath>
using namespace std;

const double eps=1e-6;
const double pi=3.141592654;

typedef class NODE
{
	public:
		double x,y;
}pos;

int n;
double PegR;  //钉子半径
pos Peg;  //钉子坐标

int precision(double x);  //精度讨论
double det(double x1,double y1,double x2,double y2);  //叉积
double dotdet(double x1,double y1,double x2,double y2);  //点积
double cross(pos A,pos B,pos C,pos D);
double distant(pos A,pos B);  //计算距离
double angle(pos A,pos B,pos P);  //计算向量PA与PB夹角

bool IsConvexBag(pos* Vectex);  //判断输入的点集是否为凸包(本题保证了输入的点集为按某一时针方向有序)
bool IsIn(pos* Vectex); //判断圆心是否在多边形内部
bool IsFit(pos* Vectex);  //判断圆的半径是否<=其圆心到多边形所有边的最小距离

int main(void)
{
	while(cin>>n && n>=3)
	{
		cin>>PegR>>Peg.x>>Peg.y;
		pos* Vectex=new pos[n+2];  //多边形顶点坐标

		for(int i=1;i<=n;i++)
			cin>>Vectex[i].x>>Vectex[i].y;

		Vectex[0].x=Vectex[n].x;  //封闭多边形
		Vectex[0].y=Vectex[n].y;
		Vectex[n+1].x=Vectex[1].x;
		Vectex[n+1].y=Vectex[1].y;

		if(!IsConvexBag(Vectex))
			cout<<"HOLE IS ILL-FORMED"<<endl;
		else
		{
			bool flag1=IsIn(Vectex);
			bool flag2=IsFit(Vectex);

			if(flag1 && flag2)
				cout<<"PEG WILL FIT"<<endl;
			else
				cout<<"PEG WILL NOT FIT"<<endl;
		}

		delete Vectex;
	}
	return 0;
}

/*精度讨论*/
int precision(double x)
{
	if(fabs(x)<=eps)
		return 0;
	return x>0?1:-1;
}

/*计算点积*/
double dotdet(double x1,double y1,double x2,double y2)
{
	return x1*x2+y1*y2;
}

/*计算叉积*/
double det(double x1,double y1,double x2,double y2)
{
	return x1*y2-x2*y1;
}
double cross(pos A,pos B,pos C,pos D)
{
	return det(B.x-A.x , B.y-A.y , D.x-C.x , D.y-C.y);
}

/*计算距离*/
double distant(pos A,pos B)
{
	return sqrt((B.x-A.x)*(B.x-A.x)+(B.y-A.y)*(B.y-A.y));
}

/*计算角度*/
double angle(pos A,pos B,pos P)
{
	return acos(dotdet(A.x-P.x,A.y-P.y,B.x-P.x,B.y-P.y)/(distant(A,P)*distant(B,P)));
}

/*凸包判断*/
bool IsConvexBag(pos* Vectex)
{
	int direction=0;
	//保存点集Vectex的旋转方向direction   1:右手正螺旋，逆时针   -1:左手正螺旋，顺时针
	for(int i=0;i<=n-1;i++)
	{
		int temp=precision(cross(Vectex[i],Vectex[i+1],Vectex[i+1],Vectex[i+2]));

		if(!direction)   //避免最初的点出现共线的情况
			direction=temp;

		if(direction*temp<0)  //只要Vectex是凸包，那么无论Vectex的旋转方向如何，direction*temp都会>=0
			return false;
	}
	return true;
}

/*判断点与多边形的关系*/
bool IsIn(pos* Vectex)
{
	double CircleAngle=0.0;  //环绕角
	for(int i=1;i<=n;i++)  //注意重复边不计算
		if(precision(cross(Peg,Vectex[i],Peg,Vectex[i+1]))>=0)
			CircleAngle+=angle(Vectex[i],Vectex[i+1],Peg);
		else
			CircleAngle-=angle(Vectex[i],Vectex[i+1],Peg);

	if(precision(CircleAngle)==0)  //CircleAngle=0, Peg在多边形外部
		return false;
	else if(precision(CircleAngle-pi)==0 || precision(CircleAngle+pi)==0)   //CircleAngle=180, Peg在多边形边上(不包括顶点)
	{
		if(precision(PegR)==0)
			return true;
	}
	else if(precision(CircleAngle-2*pi)==0 || precision(CircleAngle+2*pi)==0)   //CircleAngle=360, Peg在多边形边内部
		return true;
	else   //CircleAngle=(0,360)之间的任意角， Peg在多边形顶点上
	{
		if(precision(PegR)==0)
			return true;
	}
	return false;
}

/*判断圆与多边形的关系*/
bool IsFit(pos* Vectex)
{
	for(int i=0;i<=n;i++)
	{
		int k=precision(fabs(cross(Peg,Vectex[i],Peg,Vectex[i+1])/distant(Vectex[i],Vectex[i+1]))-PegR);
		if(k<0)
			return false;
	}
	
	return true;
}

 

 

Sample Input

5 1.5 1.5 2.0
1.0 1.0
2.0 2.0
1.75 2.0
1.0 3.0
0.0 2.0
5 1.5 1.5 2.0
1.0 1.0
2.0 2.0
1.75 2.5
1.0 3.0
0.0 2.0
3  0.1  0.2 0.0
-0.5 1.0
0.5 -1.0
0.5 1.0
3  0.25  0.2 0.0
-0.5 1.0
0.5 -1.0
0.5 1.0
3 0.1 1.6 1.2
1.0 1.0
2.0 1.0
1.0 2.0
6 0.1 1.6 1.2
1.0 1.0
1.5 1.0
2.0 1.0
1.2 1.8
1.0 2.0
1.0 1.5
3 0.1 2.0 2.0
1.0 1.0
2.0 1.0
1.0 2.0
4  1.0  2.0 1.0
0.0 0.0
0.0 4.0
4.0 4.0
4.0 0.0
4  1.0  3.5 1.0
0.0 0.0
0.0 4.0
4.0 4.0
4.0 0.0
4  0.2  1.5 1.0
1.0 1.0
2.0 2.0
1.0 3.0
0.0 2.0
4  0.4  1.5 1.0
1.0 1.0
2.0 2.0
1.0 3.0
0.0 2.0
5  0.2  1.5 2.5
1.0 1.0
2.0 2.0
1.75 2.75
1.0 3.0
0.0 2.0
5  0.2  1.5 2.5
1.0 1.0
2.0 2.0
1.75 2.5
1.0 3.0
0.0 2.0
9 0.2 0.5 2.5
0.0 0.0
1.0 0.0
1.0 1.0
2.0 1.0
2.0 0.0
3.0 0.0
3.0 5.0
1.5 5.0
0.0 5.0
9 0.2 0.5 2.5
0.0 0.0
1.0 0.0
1.0 -1.0
2.0 -1.0
2.0 0.0
3.0 0.0
3.0 5.0
1.5 5.0
0.0 5.0
7 0.2 0.5 2.5
0.0 0.0
1.0 0.0
2.0 0.0
3.0 0.0
3.0 5.0
1.5 5.0
0.0 5.0
4 0.1 1 0.5
0 2
1 0
2 2
1 1
1

 

Sample Output

HOLE IS ILL-FORMED
PEG WILL NOT FIT
PEG WILL FIT
PEG WILL NOT FIT
PEG WILL FIT
PEG WILL FIT
PEG WILL NOT FIT
PEG WILL FIT
PEG WILL NOT FIT
PEG WILL NOT FIT
PEG WILL NOT FIT
PEG WILL FIT
PEG WILL NOT FIT
HOLE IS ILL-FORMED
HOLE IS ILL-FORMED
PEG WILL FIT
HOLE IS ILL-FORMED