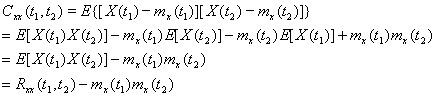与PCA相关的一些概念的集合
PCA主成分分析principle component analysis,数据预处理,对数据进行降维的重要手段。也就是分析、简化数据集。与多元统计分析理论比较密切相关。
它的一些特征:
是一个线性变换过程;
转换到一个新的坐标系统,并且求出新的坐标系统的基。
而且是一个正交变换,求出一组正交基。
新的正交基,维度一般都比源数据的维度低。
并且第一分量,正是数据在其投影上的方差最大,即新分量的方差最大。或者说,数据变化的主方向,就是协方差矩阵的主特征向量。
每一个特征值,都是与其对应分量的方差密切相关的,线性相关。特征值之和,就等于其所有点到其中心点的平方和。
比余弦变换复杂,但也比余弦变换更有效。(这个可以详细推敲下)
其算法的步骤也比较简单。一般的描述就是:
整理数据,标准化
求协方差系数
求特征值和特征向量
解释特征值和特征向量的物理意义。
但是,其推导却涉及很多数学概念,这里总结下,如果对所有概念都很熟悉,那么整体推导也就不难了。
1. 投影
投影矩阵w
W应该就特征向量组成的特征矩阵,是一个正交矩阵。可以把源数据x映射/投影到前几个分量(低维空间)的矩阵。
2. 协方差矩阵
数据标准化: 将M个特征的N个数据点,形成一个 N * M 的数据矩阵,然后去均值化。即每一数据 都减去 所在列的均值。减去均值后,仍是一个N*M的矩阵。
求这个矩阵的协方差系数。 与自己转置的协方差,矩阵,结果就是一个 N * N 的新矩阵。其实,它也是一个自相关矩阵,即B(i, j) = B(j, i), 对称阵。
为什么要去均值?
去除均值对变换的影响,而减去均值后,数据的信息量没有变化,即数据的区分度(方差)是不变的。如果不执行去均值,第一主成分,可能会或多或少的与均值相关。
为什么要选取协方差矩阵?主成分与协方差矩阵的关系?
在金融统计中又叫“方差-协方差矩阵”,它的对角元素其实就本维度数据的方差。
如果用特征值,特征向量,重新表示这个矩阵,重新表示各个维度的方差,就有点主成分与协方差矩阵的意思了。
http://zh.wikipedia.org/wiki/%E5%8D%8F%E6%96%B9%E5%B7%AE%E7%9F%A9%E9%98%B5
----
ps: 从信号来看
自相关函数
自协方差函数,其实是一阶混合中心矩
所以,自相关,与自协方差,描述表达不同,但包含的性质基本相同。自协方差是时间序列中的概念。
3. 最大化方差,谁的方差?如何做到?
向量中的一个变量,就对应于一个特征采集到的数据,所有样本的这个特征的数据形成一个集合,这个特征的方差越大,其特征的区分度就越高,越有效。
所以,就是求主成分(特征)的方差,第一主成分,就是方差最大的那个特征,第二、三。。。就类推。
有主成分,就有次要成分了。方差较小的变量特征(维度),就是次要特征。
4. 拉格朗日问题,拉格朗日求解法。约束条件,问题描述。
5. 如何选取主成分
以方差为准,一般先计算出总方差,然后给出一个比例,当主成分的方差之和大于这个比例时,就不再增加主成分的个数。
其他涉及的概念:
线性判别分析
最优类别可分离性
PCA与神经网络的关系
PCA类似于一个线性人工神经网络ANN,神经元的激活函数是线性的,隐含层K个神经元的 权重向量 收敛后, 将形成一个由前K个主成分跨越空间的基础。但是PCA 一定会产生一个正交向量组,而神经网络不一定会形成正交向量。
PCA的应用方法:
opencv中专门提供了一个PCA类,来实现主成分分析功能。
PCA的初始化需要 准备数据源,数据格式,及主成分的数目。默认保留所有成分。
project函数是将 数据 投影 到新的空间。
backproject反投影 是project的逆操作,不过,若主成分小于原维度,反投影的数据是不等于源数据的。
PCA的应用范围:
PCA只针对高斯分布的数据比较有效。
PCA要求特征的均值大致为0, 且不同特征的方差大致近似。对有的数据,需要进行白化处理,而对于自然的图像,语音,就无需处理进行方差处理,因为它们天然满足这些条件,有时要根据具体场景进行分析。
ICA 独立成分 分析
针对其他分布的数据样本,ICA是另外一种主成分分解的方法。
ICA的目的是 获取 一组、独立、完备、基。不仅线性独立,而且是正交标准基。
我们手上只有一组数据,然后需要学习到一组基向量。
这组基向量的特征:
特征是稀疏的。 什么是稀疏? 只有很少几个非零元素,或仅有几个远大于零的元素。
正交基。将原始数据变换到新的特征空间。
新的正交基空间,其实就是更加明显的特征空间,否则变换就没有了意义。
目标函数,加正交约束:
1-范数,||x||1 = |x1| + |x2| + ... + |xn|
另外, 基的维度 肯定 是小于原数据的维度的。所以,不能走超完备基的路。
数据需要无正则白化 ZCA Whitening。为什么进行白化?
因为输入数据,特别是相邻数据(如信号,图像像素)之间是相关的,有冗余的,白化的目的就是去冗余。并且,保持特征的性质不变,相关性降低。
在经过PCA的前半部分,求出完备的基向量后,相关性已经降低。
还可以将新的特征数据缩小为原来的 1/ sqrt(lamda). 这样,新的特征数据的协方差矩阵就为单位矩阵了. 这样就相关性降低,且单位方差。这就是PCA白化。
而ZCA白化,并不降低数据维度,而仅仅是PCA白化的步骤,保留所有成分,并且,增加了一个旋转的步骤,这样仍然是单位方差。
另外一个问题,当特征值lamda较小时,肯能会除0操作,所以lamda + 一个很小的数,是正则化过程中的一个技巧,并且,具有平滑、低通的作用。
对于ICA的目标函数,一般采用梯度下降法进行计算。
ICA 还可以 最大似然估计来解释。其典型应用,就是用于盲信号分析。而且ICA不适用于 高斯信号。
ICA的概念涉及更广泛,需要进一步学习。
http://zh.wikipedia.org/wiki/%E4%B8%BB%E6%88%90%E5%88%86%E5%88%86%E6%9E%90
http://baike.baidu.com/view/855712.htm
http://astrowww.bnu.edu.cn/sites/Computational_Astronomy/html/6shijian/chengguo/2008%E5%AD%A6%E7%94%9F/pca-%E5%A7%9C%E6%99%A8.pdf
opencv手册
而ZCA白化,并不降低数据维度,而仅仅是PCA白化的步骤,保留所有成分,并且,增加了一个旋转的步骤,这样仍然是单位方差。
另外一个问题,当特征值lamda较小时,肯能会除0操作,所以lamda + 一个很小的数,是正则化过程中的一个技巧,并且,具有平滑、低通的作用。