自适应滤波器(Adaptive Filter)
======= Wikipedia的解释 =======
自适应滤波器是能够根据输入信号自动调整性能进行数字信号处理的数字滤波器。作为对比,非自适应滤波器有静态的滤波器系数,这些静态系数一起组成传递函数。
对于一些应用来说,由于事先并不知道所需要进行操作的参数,例如一些噪声信号的特性,所以要求使用自适应的系数进行处理。在这种情况下,通常使用自适应滤波器,自适应滤波器使用反馈来调整滤波器系数以及频率响应。
总的来说,自适应的过程涉及到将代价函数用于确定如何更改滤波器系数从而减小下一次迭代过程成本的算法。价值函数是滤波器最佳性能的判断准则,比如减小输入信号中的噪声成分的能力。
随着数字信号处理器性能的增强,自适应滤波器的应用越来越常见,时至今日它们已经广泛地用于手机以及其它通信设备、数码录像机和数码照相机以及医疗监测设备中。
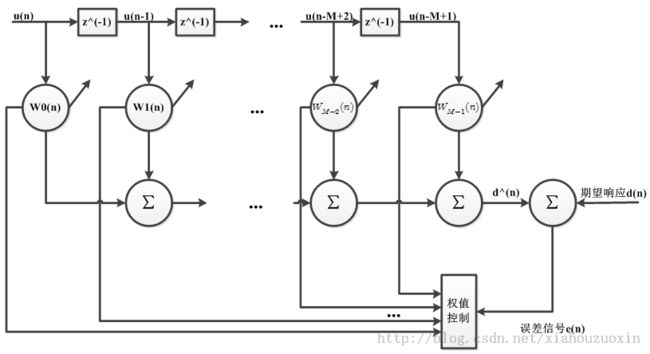
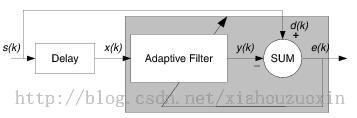
下面图示的框图是最小均方滤波器(LMS)和递归最小平方(en:Recursive least squares filter,RLS,即我们平时说的最小二乘法)这些特殊自适应滤波器实现的基础。框图的理论基础是可变滤波器能够得到所要信号的估计。
在开始讨论结构框图之前,我们做以下假设:
- 输入信号是所要信号 和干扰噪声 之和
- 可变滤波器有有限脉冲响应结构,这样结构的脉冲响应等于滤波器系数。 阶滤波器的系数定义为
- .
- 误差信号或者叫作代价函数,是所要信号与估计信号之差
可变滤波器通过将输入信号与脉冲响应作卷积估计所要信号,用向量表示为
其中
是输入信号向量。另外,可变滤波器每次都会马上改变滤波器系数
其中 是滤波器系数的校正因子。
自适应算法根据输入信号与误差信号生成这个校正因子,LMS 和 RLS 是两种不同的系数更新算法。
======= 我关于自适应滤波器及其应用的理解 =======
相对于其它类型的滤波器,自适应滤波器效果更好的关键是:自适应滤波器是反馈结构。自适应滤波器的自适应过程是:用自适应算法(Update Algorithm)调节FIR或IIR滤波器的系数,使误差信号逼近于0。
自适应滤波器的应用:
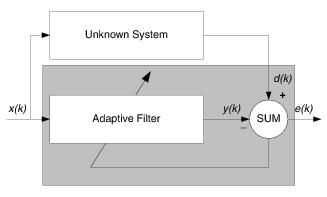
系统辨识
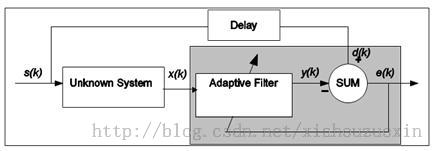
逆系统辨识
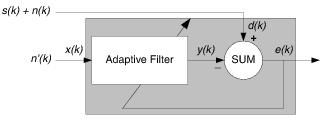
噪声消除
拟合预测
有关使用LMS算法进行线性拟合预测的内容参见博文:最小均方算法(LMS Algorithm)理论及DSP实现
对于初学者,实际问题中,比如一个不知道分布状态的声音信号,期望信号d(x)的确定很难理解,而很多文章都没有提到这点!在上面提到的自适应滤波器的4种应用中,我觉得最大的不同也在于d(x)的不同。
自己对这点也不是特别清晰,希望有识之士能提供帮助。这里暂且先做个标记!
从百度直到上找到一点答案:
1) 系统辨识:这时参考信号就是未知系统的输出,当误差最小时,此时自适应滤波器就与未知系统具有相近的特性,自适应滤波器用来提供一个在某种意义上能够最好拟合未知装置的线性模型 2) 逆模型:在这类应用中,自适应滤波器的作用是提供一个逆模型,该模型可在某种意义上最好拟合未知噪声装置。理想地,在线性系统的情况下,该逆模型具有等于未知装置转移函数倒数的转移函数,使得二者的组合构成一个理想的传输媒介。该系统输入的延迟构成自适应滤波器的期望响应。在某些应用中,该系统输入不加延迟地用做期望响应。 3) 预测:在这类应用中,自适应滤波器的作用是对随机信号的当前值提供某种意义上的一个最好预测。于是,信号的当前值用作自适应滤波器的期望响应。信号的过去值加到滤波器的输入端。取决于感兴趣的应用,自适应滤波器的输出或估计误差均可作为系统的输出。在第一种情况下,系统作为一个预测器;而在后一种情况下,系统作为预测误差滤波器。 4) 干扰消除:在一类应用中,自适应滤波器以某种意义上的最优化方式消除包含在基本信号中的未知干扰。基本信号用作自适应滤波器的期望响应,参考信号用作滤波器的输入。参考信号来自定位的某一传感器或一组传感器,并以承载新息的信号是微弱的或基本不可预测的方式,供给基本信号上。 这也就是说,得到期望输出往往不是引入自适应滤波器的目的,引入它的目的是得到未知系统模型、得到未知信道的传递函数的倒数、得到未来信号或误差和得到消除干扰的原信号
这里也有部分关于参考信号的讨论:http://www.amobbs.com/thread-5535155-1-1.html
======= Matlab代码演示 =======
自适应滤波器的函数
function [yn err] = zx_lms(xn, dn, param)
% x 输入信号
% dn 期望输出
% param Structure for using LMS, must include at least
% .w - 初始化权值
% .u - 学习率
% .M - 滤波器阶数
% .max_iter - 最大迭代次数
% .min_err - 迭代最小误差
%
% y 经过滤波器后的输出信号
% error 误差输出
W = param.w; % 初始权值
M = param.M; % 滤波器阶数
if length(W) ~= M
error('param.w的长度必须与滤波器阶数相同.\n');
end
if param.max_iter > length(xn) || param.max_iter < M
error('迭代次数太大或太小,M<=max_iter<=length(xn)\n');
end
iter = 0;
for k = M:param.max_iter
x = xn(k:-1:k-M+1); % 滤波器M个抽头的输入
y = W.*x;
err = dn(k) - y;
% 更新滤波器权值系数
W = W + 2*param.u*x;
iter = iter + 1;
if (abs(err) < param.min_err); break; end
end
% 求最优时滤波器的输出序列
yn = inf * ones(size(xn));
for k = M:length(xn)
x = xn(k:-1:k-M+1);
yn(k) = W(:,end).'* x;
end
end调用自适应滤波器实例,参考信号d(x)为正弦信号,加高斯白噪声后构成输入信号x(n),
clear all;
clc;
close all;
fs = 44100;
% x = wavread('b.wav');
t = -5*pi:pi/100:5*pi;
x = sin(t);
x = x(:);
sx = size(x,1);
subplot(2,2,1);
plot(x);axis([0 sx -1 1]);
% 原信号FFT
xf = fft(x,1024);
subplot(2,2,3);
plot(abs(xf));
% 添加高斯噪声
t = 0 : 1/fs : (sx-1)/fs;
noise = 0.2*randn(size(x)); % 均值为0,方差为0.5的标准正态噪声
x1 = x + noise;
subplot(2,2,2);
plot(x1);axis([0 sx -1 1]);
% 信号加噪声后的FFT
xf = fft(x1,1024);
subplot(2,2,4);
plot(abs(xf));
% LMS自适应滤波
param.M = 50;
param.w = ones(param.M, 1) * 0.1;
param.u = 0.1;
param.max_iter = 100;
param.min_err = 0.5;
[yn err] = zx_lms(x1(:,1), x(:,1), param);
figure,
plot(yn)
ynf = fft(yn(param.M:end), 1024);
figure,
plot(abs(ynf));
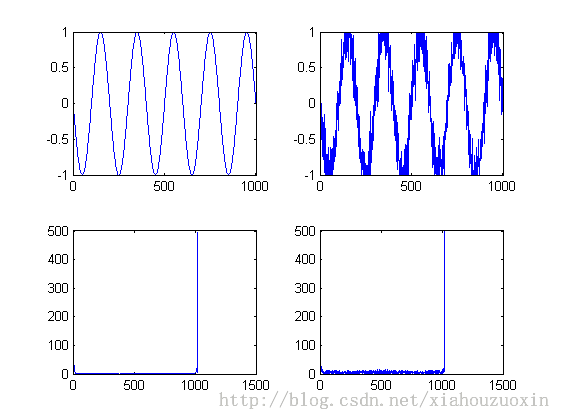
使用LMS自适应滤波器前原始信号和加高斯白噪声后的信号(时域+频域)如下,
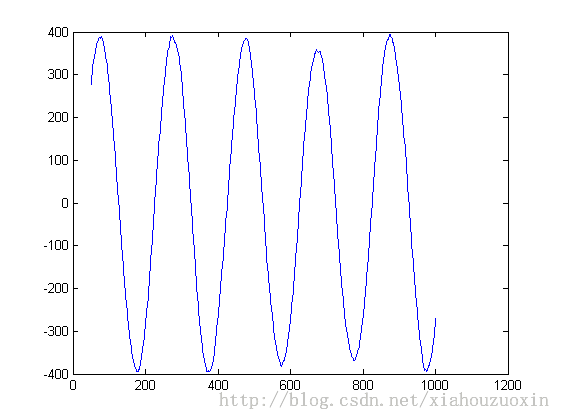
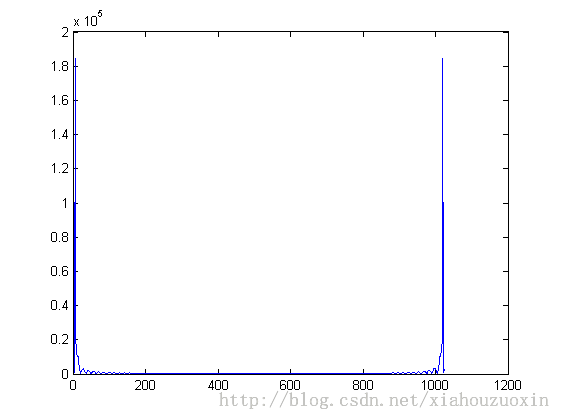
使用LMS对添加了高斯白噪声的信号滤波后效果如下,