算法——基本的图算法：广度优先搜索、深度优先搜索

图的表示

    对于图，其中和分别表示边数和节点数。图有两种表示方法：邻接链表和邻接矩阵。

邻接链表法：由一个包含条链表的数组所构成，每个节点都有一个链表。对于每个结点，邻接链表包含所有与结点之间有边相连的结点。

邻接矩阵法：对邻接矩阵表示来说，我们通常会将图中的结点编为，这种编号可以任意。在进行编号之后，图的邻接矩阵表示一个的矩阵予以表示，该矩阵满足下述条件：

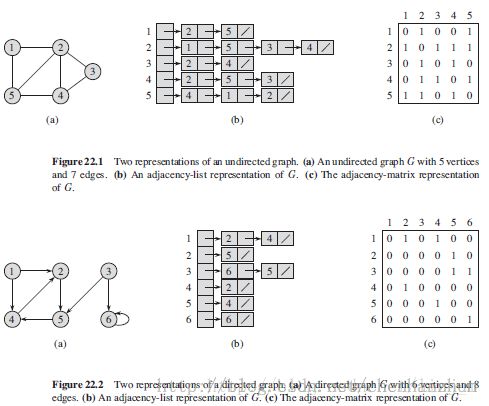
下面是两种图表示方法的结构：

广度优先搜索

   广度优先搜索（Breadth-First-Search，简称 BFS）是最简单的图搜索算法之一，也是许多重要图算法的原型。prim的最小生成树算法和Dijkstra的单源最短路径算法都使用类似广度优先搜索的思想。

　　在给定图和一个特定的源节点的情况下，广度优先搜索系统地探索中的边，以期发现可以从到达的所有节点，并计算到所有这些可达节点之间的距离（即最少的边数）。该搜索算法同时还能生成一棵根为、且包括所有的可达顶点的广度优先树。对从可达的任意节点，广度优先树中从到的路径对应于图中从到的一条最短路径，即包含最少边数的路径。该算法对有向图和无向图同样适用。之所以称为广度优先搜索，是因为它始终是将已发现和未发现节点之间的边界，沿其广度方向向外扩展。亦即，算法首先发现和距离为的所有节点，然后才会发现和距离为的其他节点。

    节点的三种状态：白色：表示未被发现的节点；黑色：表示已被发现的节点；灰色：表示已知或者未知两个集合的边界。

    节点的属性：对于任意节点，表示节点颜色，节点的前驱，属性是广度优先搜索算法计算出的从源节点到节点之间的距离。

BFS 的过程如下：

1. 初始化节点：除了源节点 s 染成灰色，其他的节点都染成白色；
2. 将源节点 s 添加到队列中（注意：该队列的所有节点都是灰色的）；
3. 从队列中取出第一个灰色节点，并将其重新染成黑色，并遍历该节点的所有白色的邻接节点，将邻接节点染成灰色并添加到队列中；
4. 判断队列是否为空：

• 若队列为空，则表示计算结束；
• 若队列不为空，则重复步骤3；

BFS(G,s)
	/* 对除源节点s之外的其他节点进行初始化 */
    for each vertex u ∈ G.V-{s} //除源节点s外，
		u.color = WHITE			//将所有节点涂上白色
		u.d = inf				//距离为无穷大
		u.front = NIL			//前驱为空
	s.color = Gray
	s.d = 0
	s.front = NIL
	Q = 空集
      /* 将节点s添加到队列Q中 */
	ENQUEUE(Q,s)
	while Q != 空集
             /* 从队列中取出第一个节点 */
		u = DEQUEUE(Q)
		for each v ∈ G.Adj[u]
			if v.color == WHITE
				v.color = Gray
				v.d = u.d +1
				v.front = u
				ENQUEUE(Q,v)
		u.color = BLACK

采用 BFS 在图中搜索某个节点的过程如下：

1. 首先将根节点放入队列中；
2. 从队列中取出第一个节点，并检验它是否为目标：
   • 若为目标，表示找到目标，则结束搜寻并回传结果；
   • 否则将它所有尚未检验过的直接子节点加入队列中；
3. 判断队列是否为空：
   • 若队列为空，表示图中没有欲搜寻的目标；
   • 若不为空，则重复步骤2；

深度优先搜索

    深度优先搜索的策略是尽可能的“深入”搜索一个图。总是对最近才发现的节点的出发边进行搜索，直到该节点的所有出发边被发现为止。当节点的所有出发边都被发现时，搜索则“回溯”到节点的前驱，来搜索该前驱节点的出发边。该过程一直持续到从源节点可以到达的所有节点都被发现为止。如果还存在尚未被发现的节点时，则深度优先搜索将从这些未被发现的节点中任选一个作为新的源节点，并重复同样的搜索过程。该算法重复整个过程，直到图中的所有节点都被发现为止。

    与广度优先搜索不同的是，广度优先搜索的前驱图形成一棵树，而深度优先搜索的前驱子图可能由多棵树组成，因为搜索可能从多个源节点重复进行。

    每个节点有两个时间戳：第一个是第一次被发现的时间；第二个是完成对节点邻接表搜索的时间；

DFS(G)
	for each vertex u∈ G.V
		u.color = WHITE
		u.front = NIL
	time = 0
	for each vertex u∈ G.V
		if u.color == WHITE
			DFS-VISIT(G,u)

DFS-VISIT(G,u)
	time = time+1
	u.d = time
	u.color = Gray
	for each vertex v∈G:Adj[u]
		if v.color == WHITE
			v.front = u
			DFS-VISIT(G,v)
	u.color = BLACK
	time = time+1
	u.f = time

         的运行过程如下：第2-4行将所有节点图为白色，将所有节点的前驱属性设置为空。第5行进行时间复位。第6-8行依次对每个节点进行检查，当发现白色节点时，则使用对节点进行访问。每次调用时，节点便成为深度优先森林中一棵树的根节点。

基于DFS的拓扑排序

    使用深度优先搜素进行拓扑排序的充要条件是必须是有向无环图，对于一个有向无环图来说，其拓扑排序的图中所有节点的一种线性次序，该次序满足以下条件：边,则节点在拓扑排序中处于节点的前面。

TOPOLOGICAL-SORT(G)
	call DFS(G) to compute finishing times v.f for each vertex v
	as each vertex is finished, insert it onto the front of a linked list
	return the linked list of vertex