Collection of algorithm for sorting. 常见排序算法集(二)

Collection of algorithm for sorting

heap sort 堆排序

               The heapsort algorithm can be divided into two parts.

               In the first step, a heap is built out of the data. The heap is often placed in an array with the layout of a complete binary tree. The complete binary tree maps the binary tree structure into the array indices; each array index represents a node; the index of the node's parent, left child branch, or right child branch are simple expressions. For a zero-based array, the root node is stored at index 0; if i is the index of the current node, then

  iParent     = floor((i-1) / 2)
  iLeftChild  = 2*i + 1
  iRightChild = 2*i + 2

如果是以 one-base array的话，root node就是

iParent  = floor(i/2);

iLeftChild = 2*i;

RightChild = 2*i+1;

我在代码实现里面就用的one-base这种方法.

             In the second step, a sorted array is created by repeatedly removing the largest element from the heap (the root of the heap), and inserting it into the array. The heap is updated after each removal to maintain the heap. Once all objects have been removed from the heap, the result is a sorted array.

             Heapsort can be performed in place. The array can be split into two parts, the sorted array and the heap. The storage of heaps as arrays is diagrammed here. The heap's invariant is preserved after each extraction, so the only cost is that of extraction.

 

heap sort C 语言实现(由于建立在堆-ADT上面，于是基于之前实现的优先队列的代码来实现的“priority_queue.h”)

堆排是一种很有意思的排序~

/***************************************************
code writer	:	EOF
code file	:	heap_sort.c
code date	:	2014.09.19
e-mail		:	[email protected]

description	:
	This is the kernel of the heap-sort.

*****************************************************/
#include "priority_queue.h"

#define DEBUG

int heap_sort(int* array,int size)
{
	struct heap* p_heap = NULL;

	p_heap = init_heap(size);
	
	if(!p_heap)
	{
		printf("initialization failed in function %s() !\n",__FUNCTION__);

		return -1;
	}

	build_heap(p_heap,array,size);

	int tmp = 0;

	for(tmp = size;tmp > 0;tmp--)
	{
		p_heap->element[tmp] = delete_heap(p_heap);
	}

	p_heap->size = size;
#ifdef DEBUG

	for(tmp = 1;tmp <=size;tmp++)
	{
		printf("%4d",p_heap->element[tmp]);
	}

	printf("\n");

#endif

	destroy_heap(p_heap);

	return 0;
}

#ifdef DEBUG
int main()
{
	int array[] = {16,14,10,8,7,9,3,2,4,1};

	int size = sizeof(array)/sizeof(array[0]);

	heap_sort(array,size);

	return 0;
}
#endif

测试结果(我用的最小堆，所以排序结果是从大到小):

这里能找到Heap的实现．

http://blog.csdn.net/cinmyheart/article/details/39371149

Merge sort 归并排序

             这里值得一提的是对于Merge的每个递归调用如果均用一个局部的临时数组，那么可以想见递归调用时，内存开销会很大，另一方面如果用Merge函数内部调用malloc去动态的开辟和释放这个数组，那么由malloc占用的时间会很多.(后面一点是我没想到的~ Mark allen weiss分析的棒呆了~)

               基于以上理由，在merge之外开辟一个大小和待排序数组大小的数组，然后把指针传入到merge函数中！

merge_sort.h

#ifndef _MERGE_SORT_H
#define _MERGE_SORT_H

	#include <stdio.h>
	#include <stdlib.h>	

	int merge(int * array,int * tmp_array,int left_pos,int right_pos,int right_end);
	
	void msort(int *array,int * tmp_array,int left,int right);

#endif

merge.c

/************************************************************
code writer	:	EOF
code date	:	2014.09.19
code file	:	merge.c

*************************************************************/
#include "merge_sort.h"

int merge(int * array,int * tmp_array,int left_pos,int right_pos,int right_end)
{
	if(!array || !tmp_array)
	{
		printf("You passed NULL in function %s()\n",__FUNCTION__);
		return -1;
	}
	
	int tmp 	= 0;
	int tmp_pos	= left_pos;
	int left_end 	= right_pos - 1;
	int num_element = right_end - left_pos + 1;
/*
	It's too expensive to call malloc for costing time.

	int *tmp_array = NULL;

	tmp_array = (int *)malloc(sizeof(int)* num_element);

	if(!tmp_array)
	{
		printf("malloc failed in function :%s()\n",__FUNCTION__);
		return 0;
	}
*/
	while(left_pos <= left_end && right_pos <= right_end)
	{
		if(array[left_pos] <= array[right_pos])
		{
			tmp_array[tmp_pos++] = array[left_pos++];
		}
		else
		{
			tmp_array[tmp_pos++] = array[right_pos++];
		}
	}
	
	while(left_pos <= left_end)
	{
		tmp_array[tmp_pos++] = array[left_pos++];
	}

	while(right_pos <= right_end)
	{
		tmp_array[tmp_pos++] = array[right_pos++];	
	}

	for(tmp = 0;tmp < num_element;tmp++,right_end--)
	{
		array[right_end] = tmp_array[right_end];
	}

/*
	free(tmp_array);	
*/

	return 0;
}

msort.c

/************************************************************
code writer	:	EOF
code date	:	2014.09.19
code file	:	msort.c

*************************************************************/
#include "merge_sort.h"

void msort(int *array,int * tmp_array,int left,int right)
{

	if(!array || !tmp_array)
	{
		printf("You passed NULL in function %s()\n",__FUNCTION__);
		return ;
	}

	if(left > right)
	{
		printf("left %d bigger than right %d\n",left,right);
	}

	int center = 0;

	/*
	**	When left == right, recursion end :)
	*/
	if(left < right)
	{
		center = (left+right)/2;

		msort(array,tmp_array,left,center);
		msort(array,tmp_array,center+1,right);
		merge(array,tmp_array,left,center+1,right);
	}
}

测试程序:

merge_sort_test.c

/************************************************************
code writer	:	EOF
code date	:	2014.09.19
code file	:	merge_sort_test.c

description:
	Code for test function msort() :)

*************************************************************/
#include "merge_sort.h"

int main()
{
	int array[] = {10,12,1,14,6,5,8,15,3,9,7,4,11,13,2};

	int size = sizeof(array)/sizeof(array[0]);

	int tmp = 0;

	int *tmp_array = NULL;
	
	tmp_array = (int*) malloc(sizeof(int)*size);

	if(!tmp_array)
	{
		printf("malloc failed in function %s()\n",__FUNCTION__);
		return 0;
	}

	msort(array,tmp_array,0,size-1);

	free(tmp_array);

	for(tmp = 0;tmp < size;tmp++)
	{
		printf("%5d",array[tmp]);
	}

	printf("\n");

	return 0;
}

update:2015.01.09

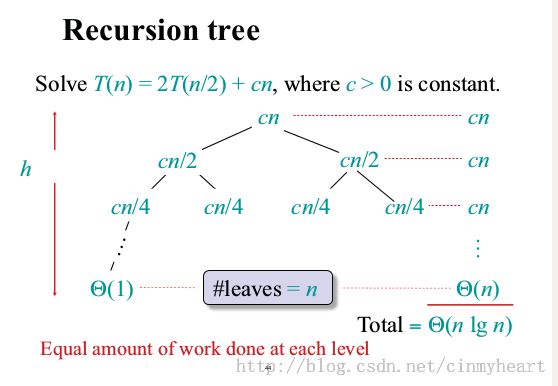
递归树分析:

从时间复杂度上看, merge sort 的nlog(n)比insert sort的 n^2要好,但是归并排序的内存开销比后者大,后者是原地排序(in place sorting)