螺旋矩阵 之二
问题
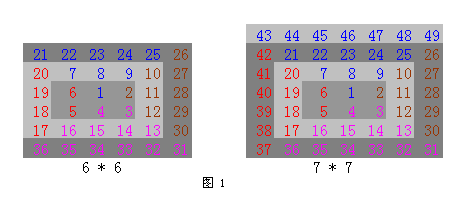
1 按顺时针方向构建(或螺旋访问)一个 n * n的螺旋矩阵,效果见下图。
2 在不构造螺旋矩阵的情况下,给定坐标 i、 j值求其对应的值 f(i, j)。
比如对 6 * 6矩阵, f(2, 0) =19 f(2, 1) = 6
思路一
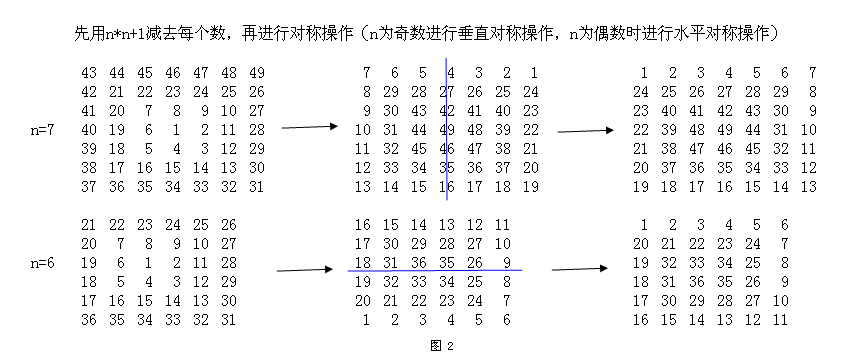
前一篇文章已经讨论了一类螺旋矩阵(由外向内) ,而这一类螺旋矩阵,则是由内向外扩散。这两类矩阵可以通过下面的方法相互转换。
由于是 n * n矩阵,对坐标( x, y)落在矩形的哪一条边上,可以直接使用 x <= y进行判断, 原来的代码 可以优化为:
int getv ( int x , int y , int n ) // 由外向内顺时针螺旋
{
if ( x <= y ) {
int k = min ( x , n - 1 - y );
return 4 * k * ( n - k ) + 1 + ( x + y - k * 2 );
}
int k = min ( y , n - 1 - x ) + 1 ;
return 4 * k * ( n - k ) + 1 - ( x + y - ( k - 1 ) * 2 );
}
int getv_in ( int x , int y , int n ) // 由内向外顺时针螺旋
{
if ( n & 1 ) return n * n + 1 - getv ( x , n - 1 - y , n );
return n * n + 1 - getv ( n - 1 - x , y , n );
}
思路二
将矩阵按 1,1,2,2, … n-1,n-1, n 个数划分成几个矩形,比如: 7*7矩阵(参考图 1):
( 1) ( 2) ( 3 4) ( 5 6) 这 6个点构成矩形 0
( 7 8 9) ( 10 11 12) ( 13 14 15 16)( 17 18 19 20) 构成矩形 1
( 21 22 23 24 25)( 26 27 28 29 30)( 31 32 33 34 35 36)( 37 38 39 40 41 42)构成矩形 2
( 43 44 45 46 47 48 49) 构成矩形 3的一条边
若对第 k ( k=0, 1, 2 … )个矩形,起始点坐标为 (i, i) ,则 i + k = floor((n-1)/2)
其右上角顶点坐标为( i, i + 2 * k + 1 )
设 t = 2 * floor((n-1)/2) + 1 = (n - 1) | 1 则右上角顶点坐标为: (i, t - i)
第 k( k=0, 1, 2 …)个矩阵的 4个顶点为(注意起始点不是左上角顶点而是 (i, i)):
(i, i-1) ----------------------------------------- (i, t-i)
| |
| |
| |
(t-i, i-1) ----------------------------------------- (t-i, t-i)
对给定的坐标(x,y),如果它落在某个这类矩形上,显然其所在的矩形起始点横坐标i满足:
i = min{x, y+1, t-x, t-y}
第k个矩形内的所有点构成(2*k+2)*(2*k+3)矩阵,共有元素P(k)=(2*k+2)*(2*k+3) 个 ,第k个矩形的起始点(i,i)对应的值为
T(i)=P(k-1)+1=2*k*(2*k+1)+1=(t-2*i)*(t-2*i-1)+1
对某个矩形,设矩形上的点(x, y)到起始点(i,i)的距离d = x-i + y-i = x+y-2*i ,设点(x, y)到下一起始点(i-1,i-1)的距离为dd,则 dd = d + 2
① 向右和向下都只是横坐标或纵坐标增加1,这两条边上的点满足f(x, y) = T(i) + d
② 向左和向下都只是横坐标或纵坐标减少1,这两条边上的点满足f(x, y) = T(i-1) –dd
对矩阵的构建和另一种螺旋矩阵类似,可参考 上一篇文章中的 代码 ,下面仅给出给定坐标求值的代码。
int getv ( int x , int y , int n ) // 螺旋矩阵(由内向外扩散)
{
int t = ( n - 1 ) | 1 ;
if ( x <= y ) {
int k = min ( x , t - y );
return ( t - 2 * k ) * ( t - 2 * k - 1 ) + 1 + ( x + y - 2 * k );
}
int k = min ( y + 1 , t - x ) - 1 ;
return ( t - 2 * k ) * ( t - 2 * k - 1 ) + 1 - ( x + y - 2 * k );
}
完整测试代码:
// 螺旋矩阵(由内向外扩散),给定坐标直接求值 by flyinghearts
//www.cnblogs.com/flyinghearts
#include<iostream>
#include<algorithm>
using std :: min ;
using std :: cout ;
int getv ( int x , int y , int n ) // 螺旋矩阵(由内向外扩散)
{
int t = ( n - 1 ) | 1 ;
if ( x <= y ) {
int k = min ( x , t - y );
return ( t - 2 * k ) * ( t - 2 * k - 1 ) + 1 + ( x + y - 2 * k );
}
int k = min ( y + 1 , t - x ) - 1 ;
return ( t - 2 * k ) * ( t - 2 * k - 1 ) + 1 - ( x + y - 2 * k );
}
int main ()
{
const int M = 12 ;
for ( int k = 2 ; k < M ; ++ k ) {
for ( int i = 0 ; i < k ; ++ i ) {
for ( int j = 0 ; j < k ; ++ j ) {
cout . width ( 4 );
cout << getv ( i , j , k ) << " " ;
}
cout << "/n" ;
}
cout << "/n" ;
}
}
作者: flyinghearts
出处: http://www.cnblogs.com/flyinghearts/
本文采用知识共享署名-非商业性使用-相同方式共享 2.5 中国大陆许可协议 进行许可,欢迎转载,但未经作者同意必须保留此段声明,且在文章页面明显位置给出原文连接,否则保留追究法律责任的权利。