微策略2011校园招聘笔试题(找出数组中两个只出现一次的数字)
1、8*8的棋盘上面放着64个不同价值的礼物,每个小的棋盘上面放置一个礼物(礼物的价值大于0),一个人初始位置在棋盘的左上角,每次他只能向下或向右移动一步,并拿走对应棋盘上的礼物,结束位置在棋盘的右下角,请设计一个算法使其能够获得最大价值的礼物。
//经典的动态规划
//dp[i][j] 表示到棋盘位置(i,j)上可以得到的最大礼物值
//dp[i][j] = max( dp[i][j-1] , dp[i-1][j] ) + value[i][j] (0<i,j<n)
int i, j, n = 8;
dp[0][0] = value[0][0];
for( i = 1 ; i < n ; i++ )
{
dp[i][0] = dp[i-1][0] + value[i][0];
}
for( j = 1 ; j < n ; j++ )
{
dp[0][j] = dp[0][j-1] + value[0][j];
}
for( i = 1 ; i < n ; i++ )
{
for( j = 1 ; j < n ; j++ )
{
dp[i][j] = max( dp[i][j-1] , dp[i-1][j] ) + value[i][j];
}
}
cout<<dp[n-1][n-1]<<endl;
扩展:现在增加一个限定值limit,从棋盘的左上角移动到右下角的时候的,每次他只能向下或向右移动一步,并拿走对应棋盘上的礼物,但是拿到的所有的礼物的价值之和不大于limit,请设计一个算法请实现。
int row,col;
int limit;
int dp[row][col][limit];
int getMaxLessLimit()
{
memset(dp,0,sizeof(dp));
for(int r = row-1 ; r >= 0; r--)
{
for(int c = col-1 ; c >= 0; c--)
{
for(int l = 0 ; l <= limit; l++)
{
if(l >= matrix[r][c])
{
int max = 0;
if(r != row-1 && dp[r+1][c][l-matrix[r][c]]>max)
max = dp[r+1][c][l-matrix[r][c]];
if(c != col-1 && dp[r][c+1][l-matrix[r][c]]>max)
max = dp[r][c+1][l-matrix[r][c]];
if(max == 0 && !(r == row-1 && c == col-1))
dp[r][c][l] = 0;
else
dp[r][c][l] = max + matrix[r][c];
}
}
}
}
return dp[0][0][limit];
}
或者
int hash[row][col][limit];
int getMaxLessLimit()
{
memset(hash,0,sizeof(hash));
hash[0][0][matrix[0][0]] = 1;
for(int i = 0 ; i < row ; i++)
{
for(int j = 0 ; j < col ; j++)
{
for(int k = 0 ; k <= limit ; k++)
{
if(k >= matrix[i][j])
{
if(i >= 1 && hash[i-1][j][k-matrix[i][j]])
hash[i][j][k] = 1;
if(j >= 1 && hash[i][j-1][k-matrix[i][j]])
hash[i][j][k] = 1;
}
}
}
}
int ans = 0;
for(int k = limit; k >= 0; k--)
{
if(hash[row-1][col-1][k] && k>ans)
ans = k;
}
return ans;
}
2、有两个字符串s1和s2,其长度分别为l1和l2,将字符串s1插入到字符串s2中,可以插入到字符串s2的第一个字符的前面或者最后一个字符的后面,对于任意两个字符串s1和s2,判断s1插入到s2中后是否能够构成回文串。。
3、已知有m个顶点,相邻的两个顶点之间有一条边相连接,首尾顶点也有一条边连接,这样就构成了一个圆环。
现在有一个二维数组M[][],M[i][j]=1时,表明第i和j个节点之间有条边存在,M[i][j]=0时,表明第i和j个节点之间没有边存在,其中 M[i][i]=0,M[i][j]=M[j][i],输入为一个二维数组M[][]和顶点的个数n,试着判断该图中是否存在两个圆环,且两个圆环彼此之间没有公共点。试着实现下面这个函数:
bool IsTwoCircle(int **M,int n)
{
......
}
4、给定如下的n*n的数字矩阵,每行从左到右是严格递增, 每列的数据也是严格递增
1 3 7 15 16
2 5 8 18 19
4 6 9 22 23
10 13 17 24 28
20 21 25 26 33
现在要求设计一个算法, 给定一个数k 判断出k是否在这个矩阵中。 描述算法并且给出时间复杂度(不考虑载入矩阵的消耗)
方法一
从右上角开始(从左下角开始也是一样的),然后每步往左或往下走。
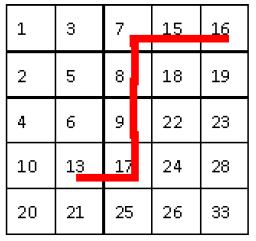
这样每步都能扔掉一行或者一列,最坏的情况是被查找的元素位于另一个对角,需要2N步,因此这个算法是o(n)的,而且代码简洁直接。
bool stepWise(int mat[][N] , int key , int &row , int &col)
{
if(key < mat[0][0] || key > mat[N-1][N-1])
return false;
row = 0;
col = N-1;
while(row < N && col >= 0)
{
if(mat[row][col] == key ) //查找成功
return true;
else if(mat[row][col] < key )
++row;
else
--col;
}
return false;
}
方法二(分治法)
首先,我们注意到矩阵中的元素总是把整个矩阵分成四个更小的矩阵。例如,中间的元素9把整个矩阵分成如下图所示的四块。由于四个小矩阵也是行列有序的,问题自然而然地划分为四个子问题。每次我们都能排除掉四个中的一个子问题。假如我们的查找目标是21,21>9,于是我们可以立即排除掉9左上方的那块,因为那个象限的元素都小于或等于9。
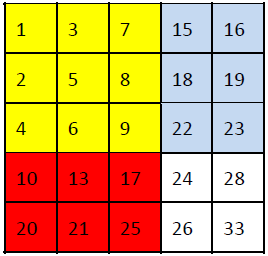
以下是这种二维二分的代码,矩阵的维度使用l、u、r、d刻画的,其中l和u表示左上角的列和行,r和d表示右下角的列和行。
bool quadPart(int mat[][N] , int key , int l , int u , int r , int d , int &row , int &col)
{
if(l > r || u > d)
return false;
if(key < mat[u][l] || key > mat[d][r])
return false;
int mid_col = (l+r)>>1;
int mid_row = (u+d)>>1;
if(mat[mid_row][mid_col] == key) //查找成功
{
row = mid_row;
col = mid_col;
return true;
}
else if(l == r && u == d)
return false;
if(mat[mid_row][mid_col] > key)
{ // 分别在右上角、左上角、左下角中查找
return quadPart(mat , key , mid_col+1 , u , r , mid_row , row , col) ||
quadPart(mat , key , l , mid_row+1 , mid_col , d , row , col) ||
quadPart(mat , key , l , u , mid_col , mid_row , row , col) ;
}
else
{ // 分别在右上角、左下角、右下角中查找
return quadPart(mat , key , mid_col+1 , u , r , mid_row , row , col) ||
quadPart(mat , key , l , mid_row+1 , mid_col , d , row , col) ||
quadPart(mat , key , mid_col+1 , mid_row+1 , r , d , row , col) ;
}
}
bool quadPart(int mat[][N] , int key , int &row , int &col)
{
return bool quadPart(mat , key , 0 , 0 , N-1 , N-1 , row , col);
}
5、设 一个64位整型n,各个bit位是1的个数为a个. 比如7, 2进制就是 111, 所以a为3。
现在给出m个数, 求各个a的值。要求代码实现。
思路:如果可以直接用stl的bitset。算法可用移位和&1来做。还有一个更好的算法是直接位与(x-1)直到它为0。
while(n)
{
n = n & (n-1);
++count;
}
6、有N+2个数,N个数出现了偶数次,2个数出现了奇数次(这两个数不相等),问用O(1)的空间复杂度,找出这两个数,不需要知道具体位置,只需要知道这两个值。
求解:如果只有一个数出现过奇数次,这个就比较好求解了,直接将数组中的元素进行异或,异或的结果就是只出现过奇数次的那个数。
但是题目中有2个数出现了奇数次?,求解方法如下:
假设这两个数为a,b,将数组中所有元素异或结果x=a^b,判断x中位为1的位数(注:因为a!=b,所以x!=0,我们只需知道某一个位为1的位数k,例如0010 1100,我们可取k=2或者3,或者5),然后将x与数组中第k位为1的数进行异或,异或结果就是a,b中一个,然后用x异或,就可以求出另外一个。
为什么呢?因为x中第k位为1表示a或b中有一个数的第k位也为1,假设为a,我们将x与数组中第k位为1的数进行异或时,也就是将x与a外加上其他第k位为1的出现过偶数次的数进行异或,化简即为x与a异或,结果是b。
代码如下:
void getNum(int a[],int length)
{
int s = 0;//保存异或结果
for(int i=0;i<length;i++)
{
s=s^a[i];
}
int temp1 = s; //临时保存异或结果
int temp2 = s; //临时保存异或结果
int k=0;
while((temp1&1) == 0) //求异或结果中位为1的位数
{
temp1 = temp1>>1;
k++;
}
for(int i=0;i<length;i++)
{
if((a[i]>>k)&1) //将s与数组中第k位为1的数进行异或,求得其中一个数
{
//cout<<a[i]<<" ";
s=s^a[i];
}
}
cout<<s<<" "<<(s^temp2)<<endl; //(s^temp2)用来求另外一个数
}
7、找出数组中只出现一次的3个数。
思路类似于求解上题,关键是找出第一个来,然后借助上题结论求另外两个。
a[]数组,假设x y z为只出现一次的数,其他出现偶数次
s^=a[i] 则x^y x^z y^z 的lowbit 这三个值有一个规律,其中肯定两个是一样的,另外一个是不一样的。令flips=上述三个值的异或。因此,可以利用此条件获得某个x(或者y,或者z),循环判断的条件是 a[i]^s的lowbit==flips
解释:a[i]^s即可划分为两组,一组是lowbit与flips不同,一组是lowbit与flips相同。这样就能找到某个x,y,z,找出后,与数组最户一个值交换,利用find2,找出剩余两个。
lowbit为某个数从右往左扫描第一次出现1的位置。其实 lowbit 函数里面写成 mark = (x&(x-1))^x ; return mark ; 也是可以的,功能是一样的。
/**
** author :hackbuteer
** date :2011-10-19
**/
#include <iostream>
using namespace std;
int lowbit(int x)
{
return x & ~(x - 1);
}
void Find2(int seq[], int n, int& a, int& b)
{
int i, xors = 0;
for(i = 0; i < n; i++)
xors ^= seq[i];
int diff = lowbit(xors);
a = 0,b = 0;
for(i = 0; i < n; i++)
{
if( diff&seq[i] ) //与运算,表示数组中与异或结果位为1的位数相同
a ^= seq[i];
else
b ^= seq[i];
}
}
//三个数两两的异或后lowbit有两个相同,一个不同,可以分为两组
void Find3(int seq[], int n, int& a, int& b, int& c)
{
int i, xors = 0;
for(i = 0; i < n; i++)
xors ^= seq[i];
int flips = 0;
for(i = 0; i < n; i++) //因为出现偶数次的seq[i]和xors的异或,异或结果不改变
flips ^= lowbit(xors ^ seq[i]);
//表示的是:flips=lowbit(a^b)^lowbit(a^c)^lowbit(b^c)
//flips = lowbit(flips); 这个是多余的
//三个数两两异或后lowbit有两个相同,一个不同,可以分为两组
//所以flips的值为:lowbit(a^b) 或 lowbit(a^c) 或 lowbit(b^c)
//得到三个数中的一个
a = 0;
for(i = 0; i < n; i++)
{
if(lowbit(seq[i] ^ xors) == flips) //找出三个数两两异或后的lowbit与另外两个lowbit不同的那个数
a ^= seq[i];
}
//找出后,与数组中最后一个值交换,利用Find2,找出剩余的两个
for(i = 0; i < n; i++)
{
if(a == seq[i])
{
int temp = seq[i];
seq[i] = seq[n - 1];
seq[n - 1] = temp;
}
}
//利用Find2,找出剩余的两个
Find2(seq, n - 1, b, c);
}
//假设数组中只有2、3、5三个数,2与3异或后为001,2与5异或后为111,3与5异或后为110,
//则flips的值为lowbit(110)= 2 ,当异或结果xors与2异或的时候,得到的就是3与5异或的结果110,其lowbit值等于flips,所以最先找出来的是三个数中的第一个数:2
int main(void)
{
int seq[]={ 2,3,3,2,4,6,4,10,9,8,8 };
int a,b,c;
Find3(seq, 11, a, b, c);
cout<<a<<endl;
cout<<b<<endl;
cout<<c<<endl;
return 0;
}
8、do while(0)在宏定义中的应用。
#define XYZ \
do{...} while(0)
假设有这样一个宏定义
#define macro(condition) \
if(condition) dosomething()
现在在程序中这样使用这个宏:
if(temp)
macro(i);
else
doanotherthing();
一切看起来很正常,但是仔细想想。这个宏会展开成:
if(temp)
if(i) dosomething();
else
doanotherthing();
这时的else不是与第一个if语句匹配,而是错误的与第二个if语句进行了匹配,编译通过了,但是运行的结果一定是错误的。
为了避免这个错误,我们使用do{….}while(0) 把它包裹起来,成为一个独立的语法单元,从而不会与上下文发生混淆。同时因为绝大多数的编译器都能够识别do{…}while(0) 这种无用的循环并进行优化,所以使用这种方法也不会导致程序的性能降低。
此外,这是为了含多条语句的宏的通用性。因为默认规则是宏定义最后是不能加分号的,分号是在引用的时候加上的。
在MFC的afx.h文件里面, 你会发现很多宏定义都是用了do...while(0)或do...while(false)。
为了看起来更清晰,这里用一个简单点的宏来演示:
#define SAFE_DELETE(p) do{ delete p; p = NULL } while(0)
假设这里去掉do...while(0),
#define SAFE_DELETE(p) delete p; p = NULL;
那么以下代码:
if(NULL != p) SAFE_DELETE(p)
else ...do sth...
就有两个问题,
1) 因为if分支后有两个语句,else分支没有对应的if,编译失败。
2) 假设没有else, SAFE_DELETE中的第二个语句无论if测试是否通过,会永远执行。
你可能发现,为了避免这两个问题,我不一定要用这个令人费解的do...while, 我直接用{}括起来就可以了
#define SAFE_DELETE(p) { delete p; p = NULL;}
的确,这样的话上面的问题是不存在了,但是我想对于C++程序员来讲,在每个语句后面加分号是一种约定俗成的习惯,这样的话,以下代码:
if(NULL != p) SAFE_DELETE(p);
else ...do sth...
由于if后面的大括号后面加了一个分号,导致其else分支就无法通过编译了(原因同上),所以采用do...while(0)是做好的选择了。
如果使用名家的方法
#define SAFE_FREE(p) do {free(p);p=NULL;} while(0)
那么
if(NULL!=p)
SAFE_FREE(p);
else
do something
展开为
if(NULL!=p)
do
{ free(p);p=NULL;}
while(0);
else
do something
好了 这样就一切太平了。