动态规划--最长公共子序列
问题:已知整数序列X,Y,长度分别为m,n,求出它们的最长公共子序列。子序列的定义如下:给定一个序列X={x1, x2, …, xm},另一个序列Z={z1, z2, …, zk}是X的一个子序列,如果存在X的一个严格递增下标序列{i1, i2, …., ik},使得对于所有的j=1,2, …, k,有xij = zj。
分析:令a[i][j]代表序列X[1->i]和Y[1->j]的最长公共子序列。则可获得递推式
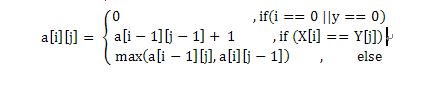
代码
#include <iostream> #define MAXLENGTH 1000 using namespace std; /** * @brief Get the longest common subsequence * * @param X[]: one sequence X. Index from 1 to m * @param Y[]: another sequence Y. Index from 1 to n * @param m: the length of X * @param n: the length of Y * @param a[][MAXLENGTH]: a[i][j] means the longest common subsequence's length of X[1->i] and Y[1->j] * @param l[][MAXLENGTH]: record the path */ void LCS(int X[], int Y[], int m, int n, int a[][MAXLENGTH], char l[][MAXLENGTH]) { for (int i = 0; i <= n; ++i) { a[0][i] = 0; } for (int i = 0; i <= m; ++i) { a[i][0] = 0; } for (int i = 1; i <= m; ++i) { for (int j = 1; j <= n; ++j) { if (X[i] == Y[j]) { a[i][j] = a[i - 1][j - 1] + 1; l[i][j] = '='; } else { if (a[i - 1][j] >= a[i][j - 1]) { a[i][j] = a[i - 1][j]; l[i][j] = '^'; } else { a[i][j] = a[i][j - 1]; l[i][j] = '<'; } } } } } /** * @brief Print the path of the longest common subsequence. * * @param b[][MAXLENGTH]: the path matrix * @param m: the rows of b[][], from 0 to m * @param n: the column of b[][], from 0 to n * @param X[]: sequence X */ void PrintSequence(char b[][MAXLENGTH], int m, int n, int X[]) { int s[MAXLENGTH]; int i = 0; while (m > 0 && n > 0) { if (b[m][n] == '=') { s[i++] = X[m]; m--; n--; } else if (b[m][n] == '<') { n--; } else { m--; } } for (int j = i - 1; j >= 0; --j) { cout << s[j]; } cout << endl; } int main() { int n, m; int X[MAXLENGTH], Y[MAXLENGTH]; int a[MAXLENGTH][MAXLENGTH]; char b[MAXLENGTH][MAXLENGTH]; while (cin >> m, cin >> n, m !=0 && n != 0) { for (int i = 1; i <= m; ++i) { cin >> X[i]; } for (int i = 1; i <= n; ++i) { cin >> Y[i]; } LCS(X, Y, m, n, a, b); cout << "Longest Common Subsequence length: " << a[m][n] << endl; PrintSequence(b, m, n, X); } }