概率图模型（PGM）学习笔记（一）动机与概述

本文根据Daphne Koller的课程整理。

PDM(ProbabilisticGraphiccal Models)

称为概率图模型。下面分别说明3个词对应的意义。

 

概率

-给出了不确定性的明确量度。

-给出了根据不确定性进行推断的有力工具。

-利用数据结构，建立了进行学习的方法，解决十分大规模的问题。

 

图

这里主要用到2种概率图，用于表示依赖关系。如图1所示。

图1

1.Bayesiannetworks

贝叶斯网络是一个有向无环图(Directed Acyclic Graph,DAG)。

由代表变量节点及连接这些节点有向边构成。节点代表随机变量，节点间的有向边代表了节点间的互相关系(由父节点指向其子节点)，用条件概率进行表达关系强度，没有父节点的用先验概率进行信息表达。

 

2.Markovnetworks

马尔可夫网络是一个无向图。

一方面它可以表示贝叶斯网络无法表示的一些依赖关系，如循环依赖；

另一方面，它不能表示贝叶斯网络能够表示的某些关系，如推导关系。

 

图形表示的优点

1.直观而紧凑的数据结构。

2.利用图形结构，提供了一套使用通用算法进行高效推断的方式。

3.能够用很少的参数表示高维的概率分布。参数的选择可以用手工也可以从数据中学习。

 

模型

模型是客观世界的陈述性描述。

 

 

举2个简单应用例子

1.医疗诊断（如图2所示）

医生面对病人时脑子里有大量的信息，这些信息都是关于如何诊断病人的指标（如发病诱因、症状、体检结果等等），医生现在需要决定到底应当如何施治。

图2就是一个真实的诊断网络。

图2

 

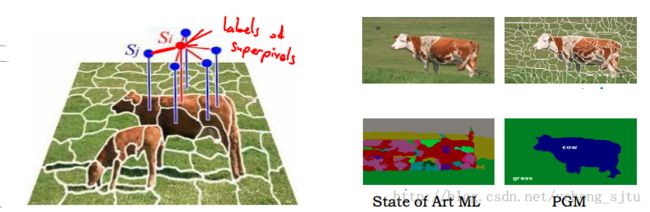
2.图像分割（如图3所示）

一副图片有成千上万个像素点或者超像素（大块的那种），需要弄清每个像素对应的内容（这些点对应的是草、天空、牛还是？）。

图中的点是随机变量，代表了像素（或者超像素）的标签，而边则代表了标签与邻近标签之间的概率关系。可以看出State of Art 的机器学习算法识别得一团糟，但是运用了PGM之后好太多了。

图3

 

这两个问题有什么共同点呢？

1.都包含了大量需要被推断的变量。

2.基本上，不论算法多么智能，能否得到正确答案，都是非常不确定的。

 

PGM的提出就是为了解决上述问题的框架。有非常广泛的应用如图4。

图4

 

家用的诊断系统

孩子生了病，家长在网站上描述病状，系统对家长提出问题。家长在回答了系统的问题之后，系统会给出孩子最有可能得的疾病。如图5所示。

图5

 

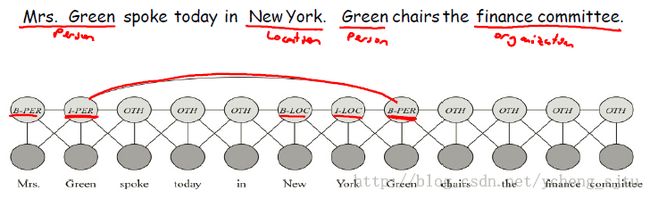
文本信息提取

将非结构型结构转成为文本中各种关键点（如人、地点、组织）之间的可能关系的表示。如图6所示。Mrs. Green这是两个词，但是要求一起识别；Green是一个词但是要识别出来它代表的是一个人，以及地点、组织等的都要通过相互之间的概率关系识别出来。如图6所示。

图6

 

总结

PGM是要做3件主要的事情：

 

1.表达

使用无向图和有向图进行表达。

使用动态和静态模型进行表达。

 

2.推断

精确推断和模糊推断（寻求计算效率和计算精度的妥协）

在不确定性状态下进行决策。

 

3.学习

自动学习参数和结构

有完全数据情形和非完全数据情形。

欢迎参与讨论并关注本博客和微博以及知乎个人主页，后续内容继续更新哦~

转载请您尊重作者的劳动，完整保留上述文字以及本文链接，谢谢您的支持！