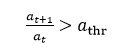Opencv2.4.9源码分析——MSCR
前面我们介绍了MSER方法,但该方法不适用于对彩色图像的区域检测。为此,Forssen于2007年提出了针对彩色图像的最大稳定极值区域的检测方法——MSCR(Maximally Stable Colour Regions)。
MSCR的检测方法是基于凝聚聚类(AgglomerativeClustering)算法,它把图像中的每个像素作为对象,通过某种相似度准则,依次逐层的进行合并形成簇,即先合并相似度大的对象,再合并相似度小的对象,直到满足某种终止条件为止。这一过程在MSCR中被称为进化过程,即逐步合并图像中的像素,从而形成斑点区域。
MSCR中所使用的相似度准则是卡方距离(Chi-squared distance):
其中,x和y分别为彩色图像中的两个不同像素,下标k表示不同的通道,例如红、绿、蓝三个颜色通道。因此公式1是一种颜色相似度的度量。
MSCR通过邻域像素之间的颜色相似度来进行聚类合并,邻域关系可以是水平垂直间邻域,也可以是还包括对角线间邻域。Opencv使用的是水平垂直间邻域,即当前像素与其右侧像素通过公式1得到一个相似度值,再与其下面像素通过公式1得到另一个相似度值。所以一般来说,每个像素都有两个相似度值,但图像的最右侧一列和最下面一行只有一个相似度值。因此对于一个大小为L×M的彩色图像来说,一共有2×L×M-L-M个相似度值。我们把这些相似度值放入一个列表中,由于该相似度是邻域之间的相似度,类似于求图像的边缘,所以该列表也称为边缘列表。
在凝聚聚类算法中,是需要逐层进行合并的。在MSCR中合并的层次也称为进化步长,用t来表示,t∈[0…T],根据经验值,T一般为200,即一共进行200步的进化过程。在每一层,都对应一个不同的颜色相似度阈值dthr,在该层只选取那些颜色相似度小于该阈值的像素进行合并。每一层的阈值是不同,并且随着t的增加,阈值也增加,因此达到了合并的区域面积逐步增加的目的。阈值的选取是关键,我们知道,图像像素邻域间的相关性是很大的,也就是通过公式1计算得到的值存在着大量的很小的值,而很大的值少之又少。因此如果我们仍然采用类似于MSER那样,随着t的增加,线性增加dthr的方法,会带来一个严重的后果,就是在进化的开始(t较小的时候),形成斑点区域的速率很快,而在进化的后期(t接近T时),形成斑点区域的速率很慢。为了解决这个问题,即在不同的进化步长下有相同的速率,对于阈值的选取,MSCR采用的是改进型的累积分布函数(CDF)的逆函数的形式。在实际应用中,事先把该函数值存储在表中,使用时通过查表的形式根据不同的t得到不同的dthr。
在每一个进化步长内,MSCR会合并一些颜色相似的像素,相邻像素之间就会组成斑点区域,对这些区域我们就需要判断其是否为最大稳定极值区域。对于所形成的斑点区域,我们需要给定该区域的面积a*和相似度阈值d*这两个参数。虽然随着进化步长t的增加,阈值dt(也就是dthr)也在增加,该区域的面积at也在增加,但只有满足两个步长间面积之比大于一定值的时候,才会重新初始化该区域的a*和d*,即:
一般athr=1.01。下面给出MSCR判断稳定区域的公式:
自从上一次初始化(即更新a*和d*)以来,如果s达到了最小值,则该区域为稳定区域。在判断稳定区域的过程中,还应该满足另外两个条件:1是公式3中的t不能是更新a*和d*之后的第一个进化步长;2是公式3中的分母部分要大于一定的阈值,即
dt - d* > mmin (4)
一般mmin设置为0.003。稳定区域通过公式3找到后,那么极值区域的判断与MSER的方法一样,是通过稳定区域的面积变量率来判断的,即上一篇文章里的公式1。
下面给出彩色图像MSCR的步骤:
1、应用公式1计算颜色相似度,得到彩色图像的边缘列表;
2、对边缘列表进行平滑处理;
3、进化处理,由各个进化步长的距离阈值得到稳定极值区域。
在opencv2.4.9中,MSCR和MSER共用一个类:
class MSER : public CvMSERParams
{
public:
// default constructor
MSER();
// constructor that initializes all the algorithm parameters
MSER( int _delta, int _min_area, int _max_area,
float _max_variation, float _min_diversity,
int _max_evolution, double _area_threshold,
double _min_margin, int _edge_blur_size );
// runs the extractor on the specified image; returns the MSERs,
// each encoded as a contour (vector<Point>, see findContours)
// the optional mask marks the area where MSERs are searched for
void operator()( const Mat& image, vector<vector<Point> >& msers, const Mat& mask ) const;
};
但MSCR比MSER多用了几个参数:
_max_evolution为进化总步长,就是参数T,一般T = 200;
_area_threshold为重新初始化的面积阈值,就是公式2中的参数athr,一般athr = 1.01;
_min_margin为最小步长距离,就是公式4中mmin,一般mmin = 0.003;
_edge_blur_size为对边缘列表进行平滑处理的孔径大小
上一篇文件已经介绍过,在MSER类中的重载( )运算符中,调用了extractMSER函数,在该函数内通过判断输入图像的类型确定是灰度图像还是彩色图像,如果是彩色图像则调用extractMSER_8UC3函数:
static void
extractMSER_8UC3( CvMat* src,
CvMat* mask,
CvSeq* contours,
CvMemStorage* storage,
MSERParams params )
{
//在应用凝聚聚类算法时,把图像中的每个像素作为一个对象,即一个节点,因此该语句是定义并分配图像节点空间
MSCRNode* map = (MSCRNode*)cvAlloc( src->cols*src->rows*sizeof(map[0]) );
//定义边缘列表的个数,即2 × L × M – L - M
int Ne = src->cols*src->rows*2-src->cols-src->rows;
//定义并分配边缘列表空间
MSCREdge* edge = (MSCREdge*)cvAlloc( Ne*sizeof(edge[0]) );
TempMSCR* mscr = (TempMSCR*)cvAlloc( src->cols*src->rows*sizeof(mscr[0]) );
//定义变量,用于由公式1计算图像每个像素颜色相似度的距离均值
double emean = 0;
//创建水平梯度矩阵,即当前像素与其右侧像素之间的差值
CvMat* dx = cvCreateMat( src->rows, src->cols-1, CV_64FC1 );
//创建垂直梯度矩阵,即当前像素与其下面像素之间的差值
CvMat* dy = cvCreateMat( src->rows-1, src->cols, CV_64FC1 );
//MSCR的预处理过程,主要完成步骤1和步骤2,后面会详细讲解
Ne = preprocessMSER_8UC3( map, edge, &emean, src, mask, dx, dy, Ne, params.edgeBlurSize );
//得到颜色相似度的距离均值
emean = emean / (double)Ne;
//对边缘列表进行升序排列,便于后面的距离阈值比较
QuickSortMSCREdge( edge, Ne, 0 );
//定义边缘列表的空间的上限
MSCREdge* edge_ub = edge+Ne;
//定义边缘列表的地址指针
MSCREdge* edgeptr = edge;
TempMSCR* mscrptr = mscr;
// the evolution process
//步骤3,进化处理,在t∈[ 0…T ]中循环,这里的i就是前面文章介绍的进化步长t
for ( int i = 0; i < params.maxEvolution; i++ )
{
//下面的4条语句用于计算当前t下的dthr值,thres为dthr
//数组chitab为事先计算好的查询表
double k = (double)i/(double)params.maxEvolution*(TABLE_SIZE-1);
int ti = cvFloor(k);
double reminder = k-ti;
double thres = emean*(chitab3[ti]*(1-reminder)+chitab3[ti+1]*reminder);
// to process all the edges in the list that chi < thres
//处理所有颜色相似度小于阈值的像素
//edgeptr < edge_ub的作用是判断边缘列表指针是否超过了列表的上限,即所指向的不是边缘
while ( edgeptr < edge_ub && edgeptr->chi < thres )
{
//由当前像素的左侧像素找到该像素所在的簇的根节点,也就是找到代表该像素所在区域的像素
MSCRNode* lr = findMSCR( edgeptr->left );
//由当前像素的右侧像素找到该像素所在的簇的根节点,也就是找到代表该像素所在区域的像素
//需要注意的是,这里的左侧和右侧并不是真正意义的左侧和右侧,它们是由preprocessMSER_8UC3函数确定的
MSCRNode* rr = findMSCR( edgeptr->right );
// get the region root (who is responsible)
//如果上面得到的两个根节点是一个节点,则不需要进行任何处理
//如果这两个根节点不是一个,则需要把它们所代表的两个区域进行合并
if ( lr != rr )
{
// rank idea take from: N-tree Disjoint-Set Forests for Maximally Stable Extremal Regions
//下面的if语句用于判断是用rr还是用lr来代表合并后的区域,并且最终通过交换来实现lr代表合并后的区域
//rank值大的根节点代表合并后的区域
if ( rr->rank > lr->rank )
{
MSCRNode* tmp;
CV_SWAP( lr, rr, tmp );
} else if ( lr->rank == rr->rank ) {
// at the same rank, we will compare the size
//如果两个根节点的rank值相同,则区域面积大的代表合并后的区域
if ( lr->size > rr->size )
{
MSCRNode* tmp;
CV_SWAP( lr, rr, tmp );
}
lr->rank++;
}
//定义rr所表示的区域的根节点为lr
rr->shortcut = lr;
//合并两个区域,合并后区域面积为两个区域面积之和
lr->size += rr->size;
// join rr to the end of list lr (lr is a endless double-linked list)
//把rr加入lr列表中,组成一个循环双链接列表
lr->prev->next = rr;
lr->prev = rr->prev;
rr->prev->next = lr;
rr->prev = lr;
// area threshold force to reinitialize
//利用公式2计算是否需要区域的重新初始化
//if语句成立,则表示需要重新初始化
if ( lr->size > (lr->size-rr->size)*params.areaThreshold )
{
//更新面积,即a*值
lr->sizei = lr->size;
//更新当前的进化步长,即t值,以区分各个层
lr->reinit = i;
//tmsr保存着上一次计算得到的稳定区域信息
if ( lr->tmsr != NULL )
{
//公式4
lr->tmsr->m = lr->dt-lr->di;
/*tmsr赋值为NULL,表示该区域已经进行了重新初始化,因此在下次进化步长并计算到该节点的时候,需要保存该区域的最大稳定极值区域;还有一个目的是避免重复计算公式4*/
lr->tmsr = NULL;
}
//更新颜色相似度值,即d*值
lr->di = edgeptr->chi;
//为公式3中的s赋予一个极小的值
lr->s = 1e10;
}
//为该区域的颜色相似度赋值
lr->dt = edgeptr->chi;
//在重新初始化以后的进化步长中,当计算到该节点时,需要进入if语句内,以判断最大稳定极值区域
if ( i > lr->reinit )
{
//公式3
double s = (double)(lr->size-lr->sizei)/(lr->dt-lr->di);
//当公式3中的s是最小值时
if ( s < lr->s )
{
// skip the first one and check stablity
// i > lr->reinit+1的目的是避免计算重新初始化后的第一个进化步长
// MSCRStableCheck函数为计算最大稳定机制区域,即计算区域面积的变化率
if ( i > lr->reinit+1 && MSCRStableCheck( lr, params ) )
{
//tmsr为NULL,表示至从上次重新初始化以来,还没有为tmsr赋值,因此这次得到的稳定区域要作为最终输出保存下来
if ( lr->tmsr == NULL )
{
//gmsr为全局稳定区域,tmsr为暂存稳定区域,mscrptr为mscr的指针变量,它是最终输出的稳定区域
lr->gmsr = lr->tmsr = mscrptr;
mscrptr++; //指向下一个地址
}
//为tmsr赋值
lr->tmsr->size = lr->size;
lr->tmsr->head = lr;
lr->tmsr->tail = lr->prev;
lr->tmsr->m = 0;
}
//保证s为最小值
lr->s = s;
}
}
}
//指向下一个边缘
edgeptr++;
}
//如果超出了边缘列表的范围,则退出for循环
if ( edgeptr >= edge_ub )
break;
}
//对最终得到的稳定区域进行裁剪,并输出
for ( TempMSCR* ptr = mscr; ptr < mscrptr; ptr++ )
// to prune area with margin less than minMargin
//公式4,判断是否满足条件
if ( ptr->m > params.minMargin )
{
//创建序列
CvSeq* _contour = cvCreateSeq( CV_SEQ_KIND_GENERIC|CV_32SC2, sizeof(CvContour), sizeof(CvPoint), storage );
//初始化该序列
cvSeqPushMulti( _contour, 0, ptr->size );
MSCRNode* lpt = ptr->head;
for ( int i = 0; i < ptr->size; i++ )
{
CvPoint* pt = CV_GET_SEQ_ELEM( CvPoint, _contour, i );
//得到稳定区域的坐标值
pt->x = (lpt->index)&0xffff;
pt->y = (lpt->index)>>16;
lpt = lpt->next;
}
CvContour* contour = (CvContour*)_contour;
cvBoundingRect( contour );
contour->color = 0;
//把坐标值压入序列中
cvSeqPush( contours, &contour );
}
//清内存
cvReleaseMat( &dx );
cvReleaseMat( &dy );
cvFree( &mscr );
cvFree( &edge );
cvFree( &map );
}
下面我们来介绍一下preprocessMSER_8UC3函数:
// the preprocess to get the edge list with proper gaussian blur
static int preprocessMSER_8UC3( MSCRNode* node, //图像像素节点
MSCREdge* edge, //边缘列表
double* total, //求相似度均值时使用,这里是所有像素相似度之和
CvMat* src, //原始图像
CvMat* mask, //掩码矩阵
CvMat* dx, //水平梯度矩阵
CvMat* dy, //垂直梯度矩阵
int Ne, //边缘列表元素的个数
int edgeBlurSize ) //平滑处理的孔径尺寸大小
{
int srccpt = src->step-src->cols*3;
uchar* srcptr = src->data.ptr; //图像当前像素指针
uchar* lastptr = src->data.ptr+3; //右侧像素指针
double* dxptr = dx->data.db; //水平梯度数据指针
//计算当前像素与其右侧像素之间的颜色相似度
for ( int i = 0; i < src->rows; i++ )
{
//图像最右侧一列没有该相似度,因此j < src->cols-1
for ( int j = 0; j < src->cols-1; j++ )
{
//公式1,计算卡方距离,保存到dx内
*dxptr = ChiSquaredDistance( srcptr, lastptr );
//地址递增
dxptr++;
srcptr += 3;
lastptr += 3;
}
//指向下一行
srcptr += srccpt+3;
lastptr += srccpt+3;
}
srcptr = src->data.ptr; //图像当前像素指针
lastptr = src->data.ptr+src->step; //下一行像素指针
double* dyptr = dy->data.db; //垂直梯度数据指针
//计算当前像素与其下面一行像素之间的颜色相似度
//图像最下面一行没有该相似度,因此i < src->rows-1
for ( int i = 0; i < src->rows-1; i++ )
{
for ( int j = 0; j < src->cols; j++ )
{
//保存到dy内
*dyptr = ChiSquaredDistance( srcptr, lastptr );
dyptr++;
srcptr += 3;
lastptr += 3;
}
srcptr += srccpt;
lastptr += srccpt;
}
// get dx and dy and blur it
//对颜色相似度值进行高斯平滑处理
if ( edgeBlurSize >= 1 )
{
cvSmooth( dx, dx, CV_GAUSSIAN, edgeBlurSize, edgeBlurSize );
cvSmooth( dy, dy, CV_GAUSSIAN, edgeBlurSize, edgeBlurSize );
}
dxptr = dx->data.db;
dyptr = dy->data.db;
// assian dx, dy to proper edge list and initialize mscr node
// the nasty code here intended to avoid extra loops
/*下面的if语句是为边缘列表赋值,如果定义了掩码矩阵,则边缘列表不保存被掩码掉的像素的边缘信息,因此边缘列表的个数Ne需要重新计算并输出。在这里我们以没有定义掩码矩阵为例进行讲解,两者的本质是一样的*/
if ( mask )
{
Ne = 0;
int maskcpt = mask->step-mask->cols+1;
uchar* maskptr = mask->data.ptr;
MSCRNode* nodeptr = node;
initMSCRNode( nodeptr );
nodeptr->index = 0;
*total += edge->chi = *dxptr;
if ( maskptr[0] && maskptr[1] )
{
edge->left = nodeptr;
edge->right = nodeptr+1;
edge++;
Ne++;
}
dxptr++;
nodeptr++;
maskptr++;
for ( int i = 1; i < src->cols-1; i++ )
{
initMSCRNode( nodeptr );
nodeptr->index = i;
if ( maskptr[0] && maskptr[1] )
{
*total += edge->chi = *dxptr;
edge->left = nodeptr;
edge->right = nodeptr+1;
edge++;
Ne++;
}
dxptr++;
nodeptr++;
maskptr++;
}
initMSCRNode( nodeptr );
nodeptr->index = src->cols-1;
nodeptr++;
maskptr += maskcpt;
for ( int i = 1; i < src->rows-1; i++ )
{
initMSCRNode( nodeptr );
nodeptr->index = i<<16;
if ( maskptr[0] )
{
if ( maskptr[-mask->step] )
{
*total += edge->chi = *dyptr;
edge->left = nodeptr-src->cols;
edge->right = nodeptr;
edge++;
Ne++;
}
if ( maskptr[1] )
{
*total += edge->chi = *dxptr;
edge->left = nodeptr;
edge->right = nodeptr+1;
edge++;
Ne++;
}
}
dyptr++;
dxptr++;
nodeptr++;
maskptr++;
for ( int j = 1; j < src->cols-1; j++ )
{
initMSCRNode( nodeptr );
nodeptr->index = (i<<16)|j;
if ( maskptr[0] )
{
if ( maskptr[-mask->step] )
{
*total += edge->chi = *dyptr;
edge->left = nodeptr-src->cols;
edge->right = nodeptr;
edge++;
Ne++;
}
if ( maskptr[1] )
{
*total += edge->chi = *dxptr;
edge->left = nodeptr;
edge->right = nodeptr+1;
edge++;
Ne++;
}
}
dyptr++;
dxptr++;
nodeptr++;
maskptr++;
}
initMSCRNode( nodeptr );
nodeptr->index = (i<<16)|(src->cols-1);
if ( maskptr[0] && maskptr[-mask->step] )
{
*total += edge->chi = *dyptr;
edge->left = nodeptr-src->cols;
edge->right = nodeptr;
edge++;
Ne++;
}
dyptr++;
nodeptr++;
maskptr += maskcpt;
}
initMSCRNode( nodeptr );
nodeptr->index = (src->rows-1)<<16;
if ( maskptr[0] )
{
if ( maskptr[1] )
{
*total += edge->chi = *dxptr;
edge->left = nodeptr;
edge->right = nodeptr+1;
edge++;
Ne++;
}
if ( maskptr[-mask->step] )
{
*total += edge->chi = *dyptr;
edge->left = nodeptr-src->cols;
edge->right = nodeptr;
edge++;
Ne++;
}
}
dxptr++;
dyptr++;
nodeptr++;
maskptr++;
for ( int i = 1; i < src->cols-1; i++ )
{
initMSCRNode( nodeptr );
nodeptr->index = ((src->rows-1)<<16)|i;
if ( maskptr[0] )
{
if ( maskptr[1] )
{
*total += edge->chi = *dxptr;
edge->left = nodeptr;
edge->right = nodeptr+1;
edge++;
Ne++;
}
if ( maskptr[-mask->step] )
{
*total += edge->chi = *dyptr;
edge->left = nodeptr-src->cols;
edge->right = nodeptr;
edge++;
Ne++;
}
}
dxptr++;
dyptr++;
nodeptr++;
maskptr++;
}
initMSCRNode( nodeptr );
nodeptr->index = ((src->rows-1)<<16)|(src->cols-1);
if ( maskptr[0] && maskptr[-mask->step] )
{
*total += edge->chi = *dyptr;
edge->left = nodeptr-src->cols;
edge->right = nodeptr;
Ne++;
}
} else {
//定义节点指针
MSCRNode* nodeptr = node;
//下面是计算图像的左上角第一个像素节点
initMSCRNode( nodeptr ); //初始化节点
//index为对应的序列值,也就是图像的坐标,纵坐标保存在高16位内,横坐标保存在低16位内
nodeptr->index = 0;
//为边缘列表的卡方距离赋值,并累加该距离值
*total += edge->chi = *dxptr;
dxptr++; //递增
edge->left = nodeptr; //边缘列表的左侧指向当前像素节点
edge->right = nodeptr+1; //右侧指向下一个像素节点
edge++; //递增
nodeptr++; //递增
//下面的for循环是计算图像的第一行像素,对应的边缘列表的卡方距离保存的是水平梯度
for ( int i = 1; i < src->cols-1; i++ )
{
initMSCRNode( nodeptr );
nodeptr->index = i;
*total += edge->chi = *dxptr;
dxptr++;
edge->left = nodeptr;
edge->right = nodeptr+1;
edge++;
nodeptr++;
}
initMSCRNode( nodeptr );
nodeptr->index = src->cols-1; //图像第一行最后一个像素
nodeptr++; //指向图像的第二行
//下面的双重for循环计算的是除了第一行和最后一行以外的像素
for ( int i = 1; i < src->rows-1; i++ )
{
initMSCRNode( nodeptr );
nodeptr->index = i<<16; //图像的第一列
*total += edge->chi = *dyptr; //垂直梯度
dyptr++;
edge->left = nodeptr-src->cols; //左侧为上面一行像素节点
edge->right = nodeptr; //右侧为当前像素节点
edge++;
*total += edge->chi = *dxptr; //水平梯度
dxptr++;
edge->left = nodeptr;
edge->right = nodeptr+1;
edge++;
nodeptr++;
for ( int j = 1; j < src->cols-1; j++ )
{
initMSCRNode( nodeptr );
nodeptr->index = (i<<16)|j;
*total += edge->chi = *dyptr;
dyptr++;
edge->left = nodeptr-src->cols;
edge->right = nodeptr;
edge++;
*total += edge->chi = *dxptr;
dxptr++;
edge->left = nodeptr;
edge->right = nodeptr+1;
edge++;
nodeptr++;
}
//图像最后一列像素
initMSCRNode( nodeptr );
nodeptr->index = (i<<16)|(src->cols-1);
*total += edge->chi = *dyptr;
dyptr++;
edge->left = nodeptr-src->cols;
edge->right = nodeptr;
edge++;
nodeptr++;
}
//图像的最后一行像素
initMSCRNode( nodeptr );
nodeptr->index = (src->rows-1)<<16;
*total += edge->chi = *dxptr;
dxptr++;
edge->left = nodeptr;
edge->right = nodeptr+1;
edge++;
*total += edge->chi = *dyptr;
dyptr++;
edge->left = nodeptr-src->cols;
edge->right = nodeptr;
edge++;
nodeptr++;
for ( int i = 1; i < src->cols-1; i++ )
{
initMSCRNode( nodeptr );
nodeptr->index = ((src->rows-1)<<16)|i;
*total += edge->chi = *dxptr;
dxptr++;
edge->left = nodeptr;
edge->right = nodeptr+1;
edge++;
*total += edge->chi = *dyptr;
dyptr++;
edge->left = nodeptr-src->cols;
edge->right = nodeptr;
edge++;
nodeptr++;
}
initMSCRNode( nodeptr );
nodeptr->index = ((src->rows-1)<<16)|(src->cols-1);
*total += edge->chi = *dyptr;
edge->left = nodeptr-src->cols;
edge->right = nodeptr;
}
return Ne;
}
下面我们再总结一下preprocessMSER_8UC3函数,首先根据公式1计算卡方距离,当前像素与其右侧像素之间的距离放在dx中,当前像素与其下面像素之间的距离放在dy中,存放的顺序都是从图像的左上角至图像的右下角。另外图像的最右一列没有dx,图像的最下一行没有dy。然后对dx和dy进行高斯平滑处理。最后创建边缘列表。边缘列表的顺序也是从图像的左上角至图像的右下角,与dx和dy的顺序完全一致,并且个数是dx与dy数量之和。如果边缘列表元素的卡方距离(edge->chi)为dx,则它的左侧(edge->left)和右侧(edge->right)分别指向的是图像的当前像素节点和它的右侧像素节点,因此对于图像的最右侧像素节点,没有dx,只有dy;如果边缘列表元素的卡方距离(edge->chi)为dy,则它的左侧(edge->left)和右侧(edge->right)分别指向的是图像的当前像素上一行像素节点和当前像素节点,因此对于图像的第一行没有dy,只有dx;图像的右上角的一个像素既没有dx,也没有dy;而其余像素节点既有dx,又有dy。
下面给出应用MSCR的应用实例:
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include <opencv2/features2d/features2d.hpp>
#include <iostream>
using namespace cv;
using namespace std;
int main(int argc, char *argv[])
{
Mat src,yuv;
src = imread("puzzle.png");
cvtColor(src, yuv, COLOR_BGR2YCrCb);
MSER ms;
vector<vector<Point>> regions;
ms(yuv, regions, Mat());
for (int i = 0; i < regions.size(); i++)
{
ellipse(src, fitEllipse(regions[i]), Scalar(255,0,0));
}
imshow("mscr", src);
waitKey(0);
return 0;
}
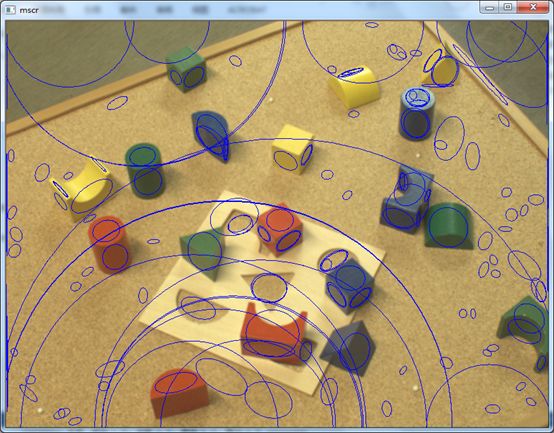
从程序中可以看出,在进行MSCR之前,需要把RGB彩色图像转换为YCrCb形式,如果直接应用RGB彩色空间,则会检测到一些不正确的区域。