白话背包之01背包
前言:这个学习笔记是去年第一次暑假集训的时候写的,时隔一年重新来看这个文章......感慨万千,点燃一根烟,下意识的摸摸自己的菊......哦不!摸摸自己的额头-----这都写的什么玩意儿!!!好吧,重新整理,希望自己以后看的时候能一目了然,如果对刚入门的童鞋有帮助那是最好不过滴
内容:
1,了解01背包以及问题所在
2,引入01背包,详细分析二维数组dp过程(结合自己画的“烂”图![]() )
)
3,分析优化的一维数组dp
一:首先关于01背包问题:
有N个物品,每个物品(只有唯一一个) i 对应有重量w[i]、价值va[i]。有一个背包可以放M重的物品,现在让你从N个物品中选择几个物品(每单个物品要么选择,要么不选择),在不超过背包上限情况使得背包装的价值最大。
分析:我们最开始接触,可能遇到以下两个问题
1,首先第一个问题:你可能很容易想到普通背包问题,也就是贪心算法,按每件物品的价值比(价值/重量)获得单件物品的性价比从大到小排序,那样就可以每次选所有物品中价值比最大的,直到背包放不下。但是不幸的是这样的做法就错啦,比如:
N = 3,背包容量 M = 7:
价值 重量 价值比
物品1 5 5 1
物品2 3 1 3
物品3 4 2 2
按贪心算法,我们会先取 物品2,然后取物品3,收益为7....背包还剩空间7-1-2=4然后就放不下重量为5的物品1啦。但是很明显的就是这不是收益最大的方法,你可以选物品1、2,收益为8,也不会超空间,也可以选择物品1、3.....反正你就是错啦。
2,然后就是第二个问题:那么很明显,这N个物品(每件选或不选)可以组成的情况用排列组合就可以知道:情况有 2*2*2*......也就是2^N种情况,成指数级,难不成你想枚举所有的情况吗?(扯蛋的废话请忽略![]() :这比N^2复杂度还要大,不信咱算算,N=1时:2^1=2,1^2=2,诶.....好像哪里不对劲,再来看看,N=3时:2^3=8,3^2=9....诶我嘞个去...怎么情况相反了是咋回事。我数学不好,你别骗我呀......)
:这比N^2复杂度还要大,不信咱算算,N=1时:2^1=2,1^2=2,诶.....好像哪里不对劲,再来看看,N=3时:2^3=8,3^2=9....诶我嘞个去...怎么情况相反了是咋回事。我数学不好,你别骗我呀......)
----------------------------------------------------------------------------------------------------
二:于是这里我们引进了01背包:
1,首先,动态规划都有一个状态转移方程(自己开始老是理解不了),等会先给出,然后结合例子说
2,有一个一维(叫做“滚动数组”)的数组还有一个二维的数组,这里先从二维的写起,个人觉得起步时理解二维的要容易!!
状态转移方程:dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+va[i]); 那么先解释这个方程的意思,开始没懂不要紧,后面结合图表理解。。dp[i][j]表示:把第 i 件物品放入空间大小为 j 的背包的最大价值 ,w[i]表示第 i 件物品的重量,va[i] 表示第 i 件物品的价值;
那么这里先稍微注意一下 dp[i-1],我们理解为:没放第i件物品的状态。从动态方程容易看出,每考虑一件物品dp[i],是依赖前面已有的情况dp[i-1]来确定的,正是因为这样,才让复杂度从指数级得以优化
下面给出这个二维数组的计算过程:(开始没理解也不要紧,可以看看循环的作用)
memset(dp,0,sizeof(dp));
for(i=1;i<=N;i++) //这里枚举每一个物品 w[i]表示第i个物品的重量,va[i]表示第i个物品的价值
for(j=1;j<=M;j++) //考虑背包容量的每一种情况
{
if(w[i]<=j) //容量j都比物品i重量少,放都放不进去我们就不要考虑啦。。。
{
if(dp[i-1][j]<dp[i-1][j-w[i]]+va[i]) //满足动态转移方程
dp[i][j]=dp[i-1][j-w[i]]+va[i];
else
dp[i][j]=dp[i-1][j];
}
else
dp[i][j]=dp[i-1][j];
}那么这个代码马上可以优化为:
for(i=1;i<=N;i++)
for(j=w[i];j<=M;j++) //也可以for(j = M; j >= w[i]; j--) 反向来也一样,下面模拟就用反向的for循环
{
if(dp[i-1][j]<dp[i-1][j-w[i]]+va[i])//这里就是dp[i][j]状态转移方程取最大的过程
dp[i][j]=dp[i-1][j-w[i]]+va[i];
else
dp[i][j]=dp[i-1][j];
}
下面模拟过程:
例子:4个物品、背包上限6第一个:w[1]=1、va[1]=4
第二个:w[2]=2、va[2]=6
第三个:w[3]=3、va[3]=12
第四个:w[4]=2、va[4]=7
下面就是dp[i][j]数组的图表:并且初始化为0(这里并没有全部填写为0,实际上是全部填写为0啦)
 此时(结合代码)是for循环的开始,第一个我们要填充的就是dp[1][6](图中黑色圈圈标记的格子),也就是求:用第1个物品放入背包空间为6的最大值,按照上面的方程,这个最大值是从
此时(结合代码)是for循环的开始,第一个我们要填充的就是dp[1][6](图中黑色圈圈标记的格子),也就是求:用第1个物品放入背包空间为6的最大值,按照上面的方程,这个最大值是从
dp[0][6]和dp[0][6-w[1]]+va[i]两个值中选出来:
那么选择之后便是:(最大值是dp[1][5]+4,也就是4)
 接着继续填充下一个j=M之后的j--的格子,也就是dp[1][5],依此填完这一列之后的结果:
接着继续填充下一个j=M之后的j--的格子,也就是dp[1][5],依此填完这一列之后的结果:
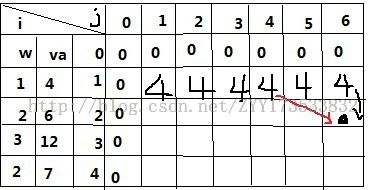 之后就填写第二行的,并且注意,填写的格子的值由两根线指向中选择,但红色的那根线是 dp[2][6-w[2]]还要加上一个va[2]的值,然后和dp[1][6]比较,选择较大的值填入,那么这一行填完的结果便是:
之后就填写第二行的,并且注意,填写的格子的值由两根线指向中选择,但红色的那根线是 dp[2][6-w[2]]还要加上一个va[2]的值,然后和dp[1][6]比较,选择较大的值填入,那么这一行填完的结果便是:
 这里也有一个地方要注意,我们有一个格子dp[2][1]没有填写,因为第二个for循环的结束条件就是j>=w[i],解释为背包的容量大于等于 i 物品的重量才去放,不然你放都放不进就没有必要放啦。
这里也有一个地方要注意,我们有一个格子dp[2][1]没有填写,因为第二个for循环的结束条件就是j>=w[i],解释为背包的容量大于等于 i 物品的重量才去放,不然你放都放不进就没有必要放啦。
那么等到最后,结果便是下面:
 红色的就是没有填写过的,也就是初始化的值为0,只是在开始没有全部填写上0,最后,dp[4][6]的意思就是把4个物品都尝试放入背包上限为6kg的最大价值:即23.....那么01背包就是这么实现的。
红色的就是没有填写过的,也就是初始化的值为0,只是在开始没有全部填写上0,最后,dp[4][6]的意思就是把4个物品都尝试放入背包上限为6kg的最大价值:即23.....那么01背包就是这么实现的。
--------------------------------------------------------------
小结:如果仔细看了上面的过程的话,那么多多少少应该有些理解过程了吧 !那么总结一下,本次总结解决状态转移方程的含义,至于for循环的实现过程应该在模拟的过程都明白了吧
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+va[i]),用我们的那种 j 从M递减到 w[i]的方式,可以这样理解:最开始,背包里什么都没放,然后我们考虑背包容量为M到w[i]的情况(小于w[i]的意思就是背包装不下去,就没必要考虑),对于一个容量 为 j 的背包A,考虑第i 个物品,它当前有一个值dp[i][j](最开始什么都没放都是0),然后我们就想 如果我们找一个容量为 j-w[i]的背包B装 第 i个物品,意思是装第 i件物品使得背包B容量为 j(可以这样看:那个背包B原来状态为dp[i-1][j-w[i]] ,现在放入i 物品,状态变为dp[i][ j ] ),那么,对于B,它现在的价值就是原来价值dp[i-1][j-w[i]]加上刚装进的 i 的价值 va[i],那么现在就做一个选择,是A的价值多还是B的价值多,我们就选择价值多的更新A,如果B大就为B,因为我们可以找到一个背包B,使得达到相同的背包容量 j 的时候价值更大。
——-------------------------------------------------------------------------
三:那么,如果比较清楚上面的实现过程啦...就可以初步了解用一维数组(既滚动数组)
仔细理解上面的过程,不难发现,我们每填写一行的时候,都是根据上一行的两个格子俩确定的...那么可以想象:我们用二维数组是不是浪费空间了呢?
那么 先来看看一维的状态转移方程:dp[j]=max(dp[j],dp[j-w[i]]+va[i]);表示:把第i个物品放入背包容量为j的背包的最大价值,
实现过程代码:
for(i=1;i<=N;i++)//注意这里只是对空间进行优化,而两个for循环是一定的 for(j=M;j>=w[i];j--) //循环顺序只能这样 if(dp[j]<dp[j-w[i]]+va[i]) dp[j]=dp[j-w[i]]+va[i];
那么现在也来模拟一下
还是上面的例子:4个物品、背包上限6
第一个:w[1]=1、va[1]=4
第二个:w[2]=2、va[2]=6
第三个:w[3]=3、va[3]=12
第四个:w[4]=2、va[4]=7
当进行第一行填写的时候,如下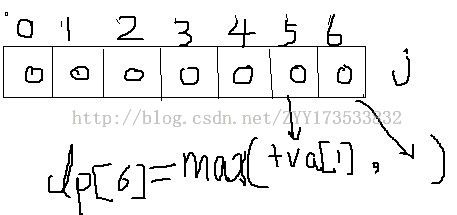 填完第一个后
填完第一个后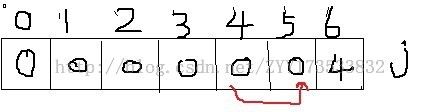 之后的每次 就用 dp[j]和dp[j-w[i]]+va[i]比较,选择大的更新dp[j],这样就可以节省很大的空间,
之后的每次 就用 dp[j]和dp[j-w[i]]+va[i]比较,选择大的更新dp[j],这样就可以节省很大的空间,
那么,值得注意的便是,用一维数组,j 只能从M到w[i] 递减,为什么呢?每次比较都是用本身dp[j],和前面的dp[j-w[i]]比较,并且值更新dp[j]的值, 那么,对于这一次的for循环,开始更新dp[j],随后j--,要填写和更新的dp[j]并没有受到刚刚的影响(这个容易懂吧......)但是一旦 j 像二维dp那样从1 到M递增,填写后面的数值很明显就被前面的影响啦
ps:最后给几个我最近做的01背包题目 首先最最简单的裸题:poj3624、然后有一个poj3628,还有一个hdu1864,还有一个poj3211,个人认为这几个题目的顺序就是难度上升的梯度