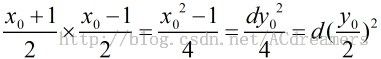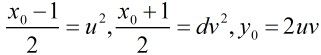关于丢番图方程x^2-dy^2=-1
我们知道丢番图方程![]() ,其中d是非完全平方正整数,那么此方程就是Pell方程,到目前为止对于它的最优求解方
,其中d是非完全平方正整数,那么此方程就是Pell方程,到目前为止对于它的最优求解方
法就是经典的连分数问题。可以看这里:http://blog.csdn.net/acdreamers/article/details/8529686
那么对于上述的Pell方程来说,它一定是有解的,而现在我们研究另一个丢番图方程:
![]() ,其中同样要求d是非完全平方正整数,对于这个方程,它就不一定有解了。
,其中同样要求d是非完全平方正整数,对于这个方程,它就不一定有解了。
那么我们来研究如下一个结论:
设![]() ,当
,当![]() 并且
并且![]() 为素数,那么
为素数,那么![]() 一定有正整数解。
一定有正整数解。
下面我们就来简略证明一下这个结论
证明:我们知道对于方程![]() 一定有正整数解,当然本文讨论中的所有
一定有正整数解,当然本文讨论中的所有![]() 都是非完全平方正整数。
都是非完全平方正整数。
假设![]() 是方程
是方程![]() 的最小正整数解,显然
的最小正整数解,显然![]() 一奇一偶,假设
一奇一偶,假设![]() ,
,![]() ,
,
那么就得到矛盾![]() ,所以只能是
,所以只能是![]() ,
,![]()
那么这样可以知道 都是整数,并且都相差1,所以必有一奇一偶,所以
都是整数,并且都相差1,所以必有一奇一偶,所以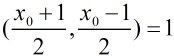
(还有一种情况不符合舍去)。那么![]() 就是方程
就是方程![]() 的最小正整数解。我们可以发现这样的做法就是根据
的最小正整数解。我们可以发现这样的做法就是根据
![]() 方程的最小正整数解来求
方程的最小正整数解来求![]() 方程的最小正整数解,最后开个方就行了。
方程的最小正整数解,最后开个方就行了。
其实这种方法看起来很麻烦,我们作如下简化:
因为求方程![]() 的解是用连分数,那么我们也可以直接对方程
的解是用连分数,那么我们也可以直接对方程![]() 用连分数求解。这里的
用连分数求解。这里的![]() 还是满足
还是满足
![]()
那么我们有如下结论:
如果![]() ,并且
,并且![]() ,那么方程
,那么方程![]() 的解可以这样求:
的解可以这样求:
先把![]() 写成连分数的形式,那么我们只需要保存它的第一个循环节的部分,然后把它回带成
写成连分数的形式,那么我们只需要保存它的第一个循环节的部分,然后把它回带成![]() 的形式,那么这里的p和q就
的形式,那么这里的p和q就
是方程![]() 的最小正整数解。
的最小正整数解。
其实直接套这里的模版即可:http://blog.csdn.net/acdreamers/article/details/9531793
那么,接下我们来看一个同余方程:![]() ,其中要求
,其中要求![]() 为奇素数,且
为奇素数,且![]() ,求x的最小正整数解。
,求x的最小正整数解。
结论:先求丢番图方程:![]() 的最小正整数解
的最小正整数解![]() 的值。然后得到
的值。然后得到![]() ,那么此时方程小于p的正整数解就分
,那么此时方程小于p的正整数解就分
为什么是这样呢?我只作一点简单的描述,这个首先得从二次剩余说起。
二次剩余当中最重要的一些定理如下:
设m是正整数,若同余式![]() ,且
,且![]() ,有解,那么a叫做模m的二次剩余,否则a叫做模m的二次非剩余。
,有解,那么a叫做模m的二次剩余,否则a叫做模m的二次非剩余。
欧拉判别条件给出了模为奇素数p有解判断条件:
并且有:当a是模奇素数p的平方剩余时,同余式![]() 恰有两个小于p的正整数解。并且这两个解之和为p。
恰有两个小于p的正整数解。并且这两个解之和为p。
所以对于同余方程![]() 来说,注意
来说,注意![]() ,很明显-1一定是p的二次剩余,所以它有两个解。
,很明显-1一定是p的二次剩余,所以它有两个解。
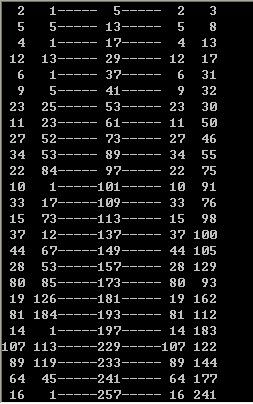
然后上面解法的正确性我给出了打表证明:http://paste.ubuntu.com/5998778/
可以从结果中看出,第一个数x用连分数和暴力求解都是一样的,解在![]() 范围内恰好有两个,而第二个数没有用,因
范围内恰好有两个,而第二个数没有用,因
为这两个解都是通过x得来的,上面的讲解都说了。
上面介绍的是连分数求方程![]() 的最小正整数解,其中
的最小正整数解,其中![]() 且p是素数。
且p是素数。
细心的读者会发现,当p很大时还是行不通,因为一是循环节太大,而是可能在求循环节时有数字超过整数范围的。
那么下面我将介绍我认为是解决这个问题的最好方法。把下面的n换为-1就是上面的方程了。
http://algo.ftiasch.com/tag/number-theory/
注意这里是在二次域上做计算的,w不是实数。