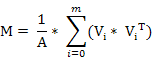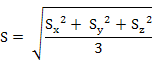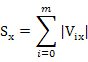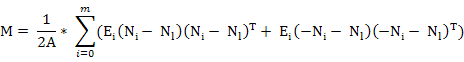三维模型的主成分分析(3D Model PCA, CPCA, NPCA)
PCA(Principal Component Analysis,主成分分析)是模型处理中常用的一种方法,因为它能够有效地提取出模型的主要成分和结构,一定程度上去除噪音和干扰,因此成为了对3D模型施加其它后续操作的基本变换。由于模型的3D自由度,因而在对模型施加PCA操作时需要满足以下几个基本要求:平移不变性,旋转不变性,缩放不变性。在进行PCA分析时,由于旋转和缩放不变性比较容易实现,因而各种方法的差别主要就集中在旋转不变性的实现上。
常用的两种模型PCA方法有CPCA和NPCA,前一种方法基于网格模型的顶点统计属性而得到旋转矩阵,后一种方法基于网格模型的表面法向量统计属性而得到旋转矩阵。
假设模型的顶点集为V,法向量集为N。
CPCA:
1. Translation Invariance
寻找模型的质心C。质心的计算就通过模型顶点集的统计,得到三个方向上顶点的均值即为质心,平移不变性的实现即是将模型的质心向坐标原点处移动至重合即可实现。
此时可得到移动后的模型为:
![]()
2. Rotation Invariance
旋转不变性的实现主要通过统计模型的顶点,进而得到旋转矩阵,然后对模型施加矩阵旋转即可。首先计算影响矩阵M:
其中的A为模型网格的总面积,m为模型顶点的数量。然后求得M的3个特征值及特征向量,然后根据其特征值的大小,依递减的顺序组合特征向量即可得到旋转矩阵RM,得到此旋转矩阵后即可对模型进行旋转,得到顶点及向量集为:
![]()
3. Scale Invariance
缩放不变性的实现是通过统计施加上述操作模型的顶点与质心之间的距离分布关系。
其中
Sy , Sz 与此类似。得到缩放矩后即可对模型施加缩放操作:
![]()
NPCA:
NPCA的实现在平移与缩放不变性的实现上均与CPCA相同,主要差别在于旋转矩阵的获得有所不同。
同样得到影响矩阵M:
其中Ei为第i个三角面的法向量,Nl为整个模型的法向量均值。之后即与上述操作相同,求得RM之后即可施加旋转操作。
对两个模型施加PCA操作:
CPCA NPCA
更多内容请参见:
《Efficient 3D Shape matching and retrieval using a concrete radialized spherical projection representation》