图 深度优先遍历 广度优先遍历 非递归遍历 图解算法过程
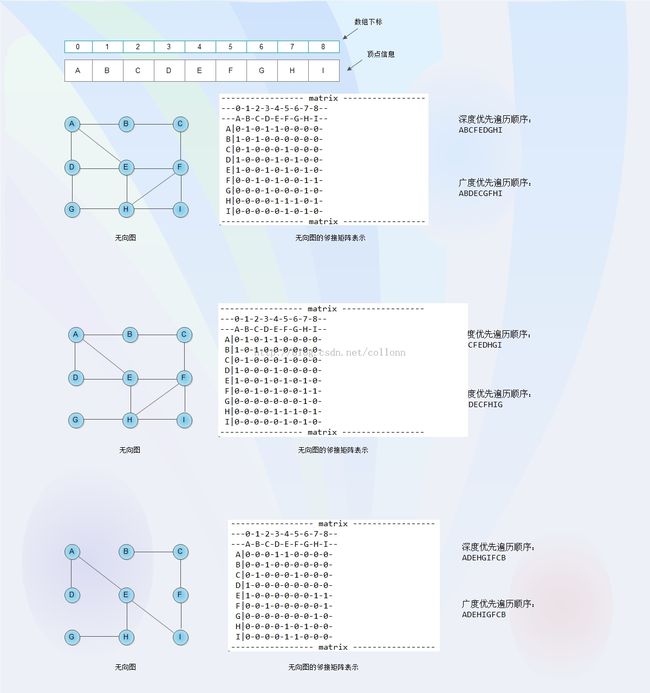
图的邻接矩阵表示
通常图的表示有两种方法:邻接矩阵,邻接表。
本文用邻接矩阵实现,一是代码量更少,二是代码风格也更贴近C语言。但不论是图的哪种实现方式,其基本的实现思想是不变的。
1:节点的信息,我们用一维数组a[n]来存储,假设图共有n个节点。
2:节点与节点间的关系,我们用二维数组b[n][n]存储。
3:b[i][j]表示,从i到j有向连通,b[j][i]表示从j到i有向连通,而当i=j时(矩阵的对角线上的元素),b[i][j]没有实际意思,在遍历时,我可以用来存储定节点是否访问过。
图的深度优先遍历
DFS类似于树的先根遍历,尽可能深的去访问节点。
DFS算法过程我们用到了递归的思想,如果还需要求出路径,可以借助栈来实现(后文会不断的实现图的各种算法)。
步骤1:访问节点,将该节点标记为已访问。
步骤2:如果节点还有未标记的邻接点,继续步骤1,否则返回。
图的广度优先遍历
BFS我们用队列来实现。
步骤1:如果队列为空,则返回,否则,取出队列头节点,将该节点标记为已访问。
步骤2:同时,将该节点所有未标记的邻接点,加入队列尾,继续步骤1。
图的非递归遍历
我们借助栈来实现。
步骤1:如果栈为空,则退出程序,否则,访问栈顶节点,但不弹出栈点节点。
步骤2:如果栈顶节点的所有直接邻接点都已访问过,则弹出栈顶节点,否则,将该栈顶节点的未访问的其中一个邻接点压入栈,同时,标记该邻接点为已访问,继续步骤1。
如下例子:
深度和广度遍历代码如下:
package com.collonn.algorithm;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
/**
* 无向图,邻接矩阵<br/>
* 深度优先遍历<br/>
* 广度优先遍历<br/>
*/
public class GrfDfsBfs {
private int total;
private String[] nodes;
private int[][] matirx;
public GrfDfsBfs(int total, String[] nodes) {
this.total = total;
this.nodes = nodes;
this.matirx = new int[total][total];
}
private void printMatrix() {
System.out.println("----------------- matrix -----------------");
System.out.println("---0-1-2-3-4-5-6-7-8--");
System.out.println("---A-B-C-D-E-F-G-H-I--");
for (int i = 0; i < this.total; i++) {
System.out.print(" " + this.nodes[i] + "|");
for (int j = 0; j < this.total; j++) {
System.out.print(this.matirx[i][j] + "-");
}
System.out.print("\n");
}
System.out.println("----------------- matrix -----------------");
}
// 设置[i][i]位置处的元素值为0,0表示图中的定点i未被访问,1表示图中的定点i已被访问
private void resetVisited() {
for (int i = 0; i < this.total; i++) {
this.matirx[i][i] = 0;
}
}
// 图的深度优先遍历(递归方法)
private void dfsRecursive(int i) {
// 如果已访问,则返回
if (this.matirx[i][i] == 1) {
return;
}
this.matirx[i][i] = 1;
System.out.print(this.nodes[i]);
for (int j = 0; j < this.total; j++) {
// i=j时,[i][j]表示节点是否被访问过,不参与dfs
if (i == j) {
continue;
}
if (this.matirx[i][j] == 1) {
dfsRecursive(j);
}
}
}
// 图的深度优先遍历(用栈实现)
private void dfsStack(Stack<Integer> stack) {
// 如果已访问,则返回
int k = -1;
while(!stack.empty()){
k = stack.peek().intValue();
boolean needPop = true;
for(int i = 0; i < this.total; i++){
if(this.matirx[k][i] == 1 && this.matirx[i][i] == 0){
stack.push(i);
this.matirx[i][i] = 1;
System.out.print(this.nodes[i]);
needPop = false;
break;
}
}
if(needPop){
stack.pop();
}
}
}
// 图的广度优先遍历
private void bfsQueue(Queue<Integer> ls) {
if (ls == null || ls.size() == 0) {
return;
}
int i = ls.poll().intValue();
// 如果已访问,则跳过该元素,继续访问队列的下一个元素
if (this.matirx[i][i] == 1) {
this.bfsQueue(ls);
return;
}
this.matirx[i][i] = 1;
System.out.print("" + this.nodes[i]);
for (int j = 0; j < this.total; j++) {
// i=j时,[i][j]表示节点是否被访问过,不参与bfs
if (i == j) {
continue;
}
//如果顶点已访问过,则不再加入队列
if (this.matirx[i][j] == 1 && this.matirx[j][j] != 1) {
ls.offer(j);
}
}
// System.out.print("\n队列元素:");
// for (Integer k : ls) {
// System.out.print(k);
// }
// System.out.println("");
this.bfsQueue(ls);
}
// 初始化图数据
// 0---1---2---3---4---5---6---7---8---
// A---B---C---D---E---F---G---H---I---
private void initGrf() {
// A-B, A-D, A-E
this.matirx[0][1] = 1;
this.matirx[1][0] = 1;
this.matirx[0][3] = 1;
this.matirx[3][0] = 1;
this.matirx[0][4] = 1;
this.matirx[4][0] = 1;
// B-C
this.matirx[1][2] = 1;
this.matirx[2][1] = 1;
// C-F
this.matirx[2][5] = 1;
this.matirx[5][2] = 1;
// D-E, D-G
this.matirx[3][4] = 1;
this.matirx[4][3] = 1;
this.matirx[3][6] = 1;
this.matirx[6][3] = 1;
// E-F, E-H
this.matirx[4][5] = 1;
this.matirx[5][4] = 1;
this.matirx[4][7] = 1;
this.matirx[7][4] = 1;
// F-H, F-I
this.matirx[5][7] = 1;
this.matirx[7][5] = 1;
this.matirx[5][8] = 1;
this.matirx[8][5] = 1;
// G-H
this.matirx[6][7] = 1;
this.matirx[7][6] = 1;
// H-I
this.matirx[7][8] = 1;
this.matirx[8][7] = 1;
}
// 初始化图数据
// 0---1---2---3---4---5---6---7---8---
// A---B---C---D---E---F---G---H---I---
private void initGrf2() {
// A-B, A-D, A-E
this.matirx[0][1] = 1;
this.matirx[1][0] = 1;
this.matirx[0][3] = 1;
this.matirx[3][0] = 1;
this.matirx[0][4] = 1;
this.matirx[4][0] = 1;
// B-C
this.matirx[1][2] = 1;
this.matirx[2][1] = 1;
// C-F
this.matirx[2][5] = 1;
this.matirx[5][2] = 1;
// D-E
this.matirx[3][4] = 1;
this.matirx[4][3] = 1;
// E-F, E-H
this.matirx[4][5] = 1;
this.matirx[5][4] = 1;
this.matirx[4][7] = 1;
this.matirx[7][4] = 1;
// F-H, F-I
this.matirx[5][7] = 1;
this.matirx[7][5] = 1;
this.matirx[5][8] = 1;
this.matirx[8][5] = 1;
// G-H
this.matirx[6][7] = 1;
this.matirx[7][6] = 1;
// H-I
this.matirx[7][8] = 1;
this.matirx[8][7] = 1;
}
// 初始化图数据
// 0---1---2---3---4---5---6---7---8---
// A---B---C---D---E---F---G---H---I---
private void initGrf3() {
// A-D, A-E
this.matirx[0][3] = 1;
this.matirx[3][0] = 1;
this.matirx[0][4] = 1;
this.matirx[4][0] = 1;
// B-C
this.matirx[1][2] = 1;
this.matirx[2][1] = 1;
// C-F
this.matirx[2][5] = 1;
this.matirx[5][2] = 1;
// E-H, E-I
this.matirx[4][7] = 1;
this.matirx[7][4] = 1;
this.matirx[4][8] = 1;
this.matirx[8][4] = 1;
// F-I
this.matirx[5][8] = 1;
this.matirx[8][5] = 1;
// G-H
this.matirx[6][7] = 1;
this.matirx[7][6] = 1;
}
public static void main(String[] args) {
String[] nodes = new String[] { "A", "B", "C", "D", "E", "F", "G", "H", "I" };
GrfDfsBfs grf = new GrfDfsBfs(9, nodes);
grf.initGrf();
grf.printMatrix();
System.out.println("------ 深度优先遍历(递归)开始 ------");
grf.resetVisited();
grf.dfsRecursive(0);
System.out.println();
System.out.println("------ 深度优先遍历(递归)结束 ------");
System.out.println("------ 深度优先遍历(栈)开始 ------");
grf.resetVisited();
Stack<Integer> stack = new Stack<Integer>();
stack.push(0);
grf.matirx[0][0] = 1;
System.out.print(grf.nodes[0]);
grf.dfsStack(stack);
System.out.println();
System.out.println("------ 深度优先遍历(栈)结束 ------");
System.out.println("------ 广度优先遍历开始 ------");
grf.resetVisited();
Queue<Integer> queue = new LinkedList<Integer>();
queue.add(0);
grf.bfsQueue(queue);
System.out.println();
System.out.println("------ 广度优先遍历结束 ------");
}
}
原创博文,转载请注明出处。
右键,查看图片,看大图。