[机器学习]信息论(Information theory)的一些point
信息论(Information theory)的一些points
①—熵(entropy)
对于一个变量X~p(X服从p分布),该变量的熵是
描述该变量的不确定性的一个值
eg:对于一个有k个状态的离散随机变量X,有
a.当log以2为底的时候称之为 bits,结果可以视为多少个二进制位可以表示该变量
b.当log以e为底的时侯称之为 nats
②—KL divergence (KL距离)
这个值是用来衡量两个分布之间相异度的,具体来说,假设有k个状态的两个离散分布p,q,则
a.如果是连续的随机变量,把∑用积分 符号替换就好了
对上式进行转化:
其中H(p,q)称为交叉熵 (cross entropy)
交叉熵可以看作是当我们用模型 q来编码来自模型p的变量时所需的平均bits(如果log以2为底的话)
所以,有有H(p)=H(p,p),所以KL距离就可以看做是:
用模型q来编码来自模型p的变量所需的额外bits!
因为是“额外的”,所以 KL的距离的值一定大于0,KL=0当且仅当p=q。
③—互信息(Mutual Information)
我们知道如果p(x,y)=p(x)p(y),则X和Y互相独立
而衡量两个随机变量的相关性有 相关系数 ,而
互信息就是用来衡量 p(x,y)与p(x)p(y)之间的关系的:
其实就是借用了上面的KL距离,可以知道
另一个有用的定义是
pointwise mutual information(PMI),是对于每个点的定义
可以
得知 MI值其实就是PMI值的期望
④—for 连续随机变量
上面都是 讲的离散随机变量 ,如果要变化到连续随机变量,则可以
把∑用积分 符号替换就好了
对于连续随机变量一个有用的参数是maximal information coefficient(MIC)
是用来告诉我们两个变量的独立性的一个系数,可以表示两个变量间的独立性
MIC值介于[0,1],0表示两个变量互相独立,而1表示两个变量有无噪(noisy-free)的关系(不仅仅是线性关系)
一个图示说明---图片来自《Machine Learning - A Probabilistic Perspective》--
左边图的 横轴是MIC,纵轴是相关系数,例如C点是相关系数接近0,MIC接近0,从右图可以看出 C的分布是没有规律的
而H或者D图,两个变量间有很强的关系,表现为基本上的线性关系 ,其它例子自己看把


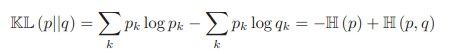

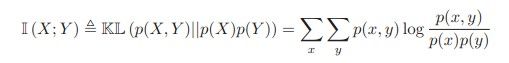


![[机器学习]信息论(Information theory)的一些point_第1张图片](http://img.e-com-net.com/image/info5/884222c20787473a8f38b1b460d8ba26.jpg)